1 地球是圆的
历史上很长的时间,人们都觉得地球是平的:
不过如果在海边,还是容易发现地球其实不是平的。比如极目远眺,发现很远的建筑在海平面以下:

加上麦哲伦环球航行、月全食、太空旅行等各种事实的呈现,人们最终可以确定地球是圆的的了(下图是从月球上看地球)。

之所以这么难发现地球是圆的,主要是因为地球的半径太大了。
2 球的曲率
下面有三个球体,网球、篮球、地球,半径越小的越容易看出是圆的:

随着半径地变大(除了圆心之外,圆能够改变的也只有半径了),越来越不圆了:
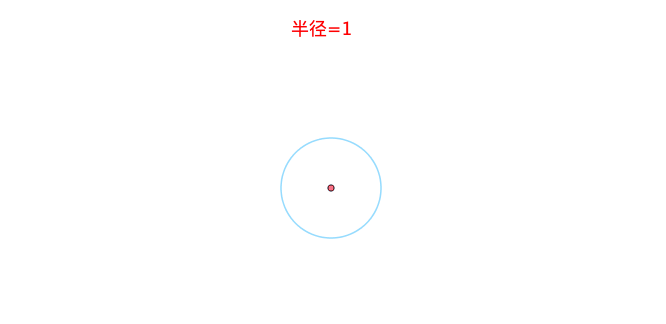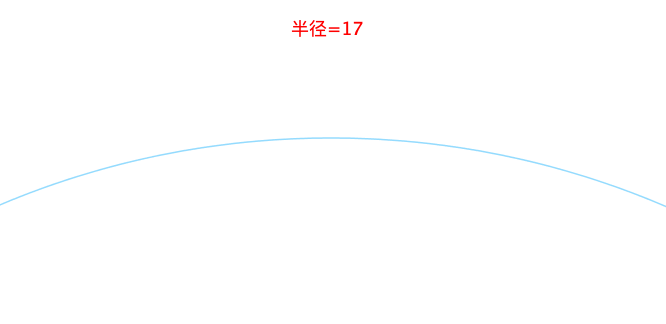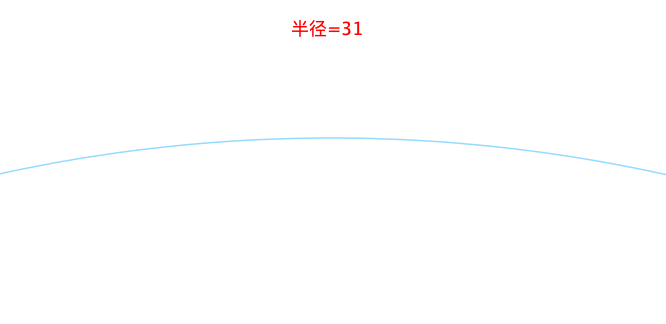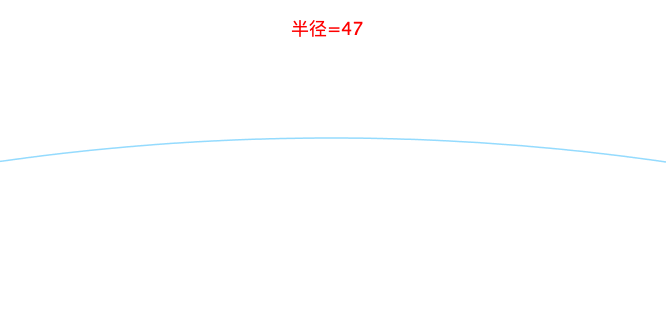
因此,定义球体或者圆的“圆”的程度,术语叫作 曲率 ,为:

其中 为球体或者圆的半径,这样半径越小的圆曲率越大,直线可以看作半径为无穷大的圆,其曲率为:
为球体或者圆的半径,这样半径越小的圆曲率越大,直线可以看作半径为无穷大的圆,其曲率为:

这样定义曲率符合我们的直觉。
3 曲线的曲率
很显然,曲线也有不同的弯曲程度:

3.1 密切圆
可以将圆的曲率扩展到曲线上。我们知道两点决定一条直线,比如下面就是曲线的割线:

当  的时候,得到的就是切线:
的时候,得到的就是切线:
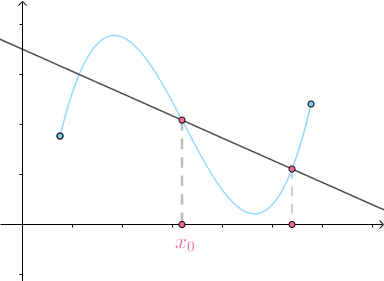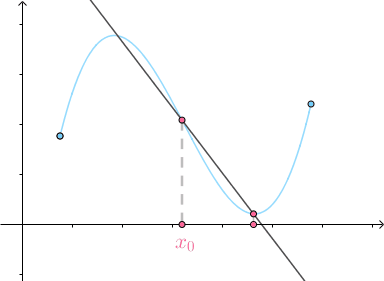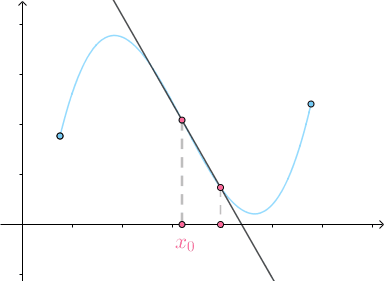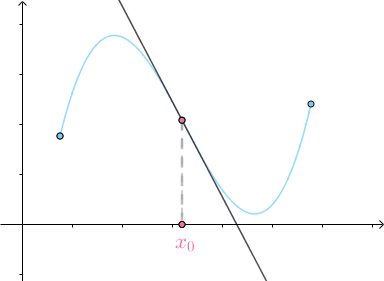
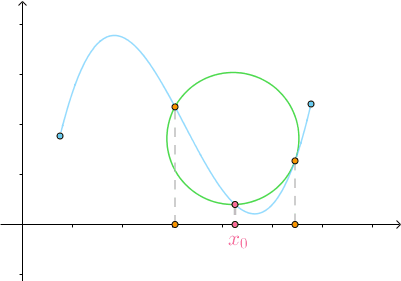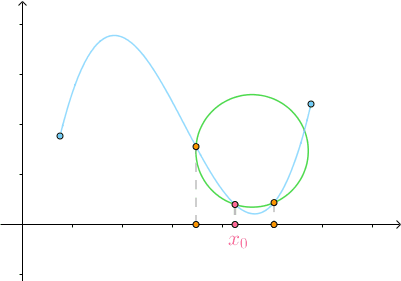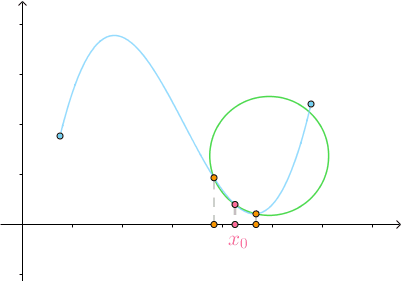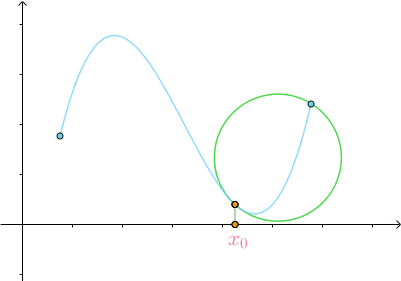
同样的道理,三个点可以确定一个圆:

当  时,得到的圆称为 密切圆 (Osculating circle),是对
时,得到的圆称为 密切圆 (Osculating circle),是对 附近的曲线的 最佳圆近似 :
附近的曲线的 最佳圆近似 :
3.2 密切圆的半径与曲率
可以观察到,在曲线较为平坦的地方,密切圆半径很大,较为弯曲的地方,密切圆半径就较小:
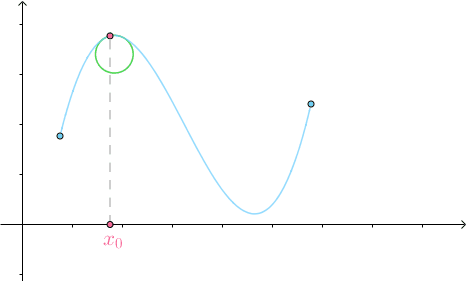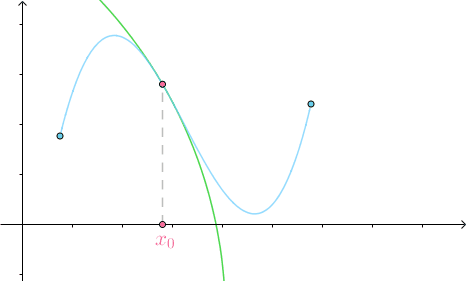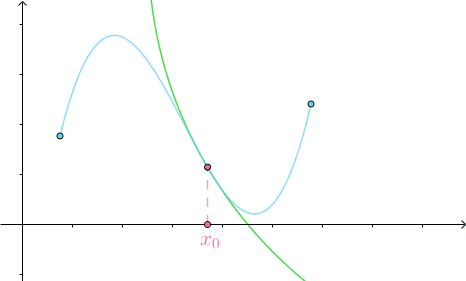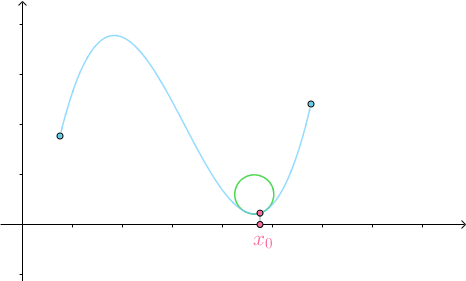
这个事实告诉我们,可以用密切圆的曲率来定义曲线的曲率(因为格式所限,详细推导请查看此处,还是挺有意思的,综合应用了线性代数的知识):
已知函数在
点有二阶导数
,且
,则此点有密切圆,其半径为:
此时,曲线的 曲率 也就是密切圆的曲率,为:
所以密切圆也称为曲线的 曲率圆 ,半径
称为 曲率半径 。
4 曲率圆的圆心
光知道半径是没有办法画出密切圆(曲率圆)的,还必须知道它的圆心在哪里(因为格式所限,详细推导请查看此处):
已知函数在
点有二阶导数
,且
,则此点有密切圆(曲率圆),其圆心为
:
值为:
此圆心也称作 曲率中心 。
如果  移动,会得到一系列曲线
移动,会得到一系列曲线  的密切圆的圆心:
的密切圆的圆心:
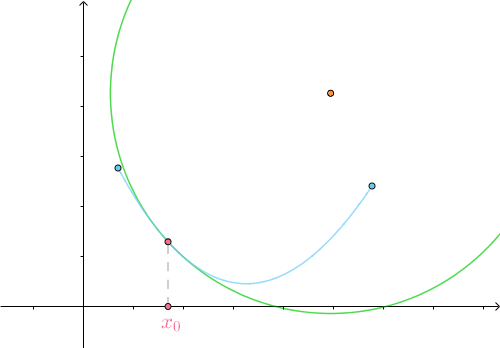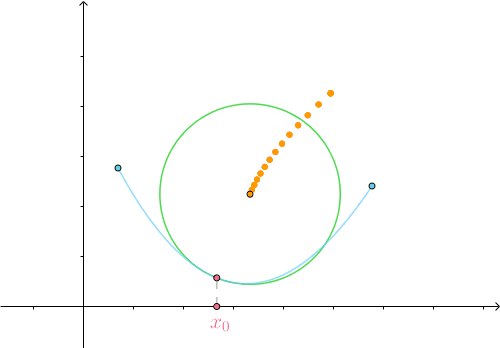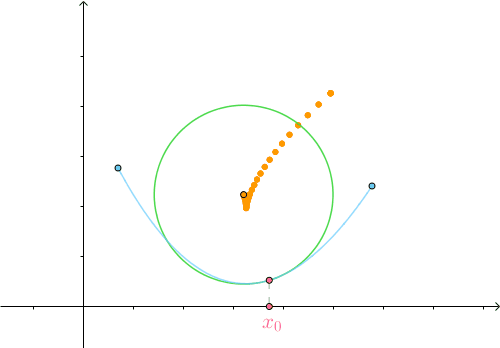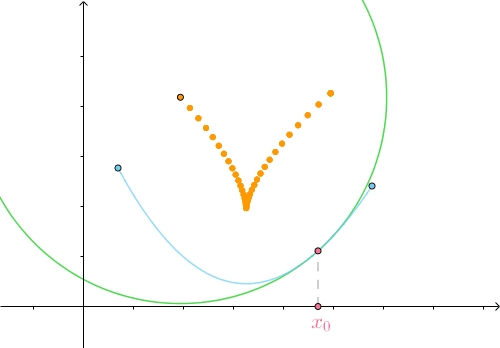
圆心轨迹  称为曲线
称为曲线  的 渐屈线 ,其参数方程很显然为:
的 渐屈线 ,其参数方程很显然为:

曲线  称为圆心轨迹
称为圆心轨迹  的 渐伸线 。
的 渐伸线 。





























 1941
1941

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










