生鲜农产品末端配送路径优化毕业论文【附代码+数据】

✅博主简介：本人擅长数据处理、建模仿真、论文写作与指导，科研项目与课题交流。项目合作可私信或扫描文章底部二维码。

---

（1）随着生鲜农产品电商的迅速发展，物流配送的效率成为了企业竞争力的重要一环。生鲜农产品由于其易腐烂、对温度敏感等特点，对配送时间的要求极高。然而，在城市物流配送中，交通拥堵等不确定性因素使得配送效率大大降低，延长了在途时间，增加了物流成本，影响了产品的新鲜度，从而降低了客户的满意度。为了解决这一问题，有必要针对交通路况进行精细化的路径规划，以确保生鲜农产品能够在最短的时间内到达消费者手中，保持良好的品质。

以S企业为例，本文对其生鲜农产品末端配送路径进行了深入分析。S企业的物流配送面临的问题主要集中在以下几点：首先，现有的配送路径规划方法未能充分考虑实时的交通状况，导致在高峰时段配送延误频繁发生；其次，配送路线的选择缺乏灵活性，常常沿用固定路径，而未根据实际路况进行动态调整；此外，配送过程中产生的各种成本，如运输成本、蓄冷成本、货损成本等未能得到有效控制。因此，如何优化末端配送路径，在降低配送成本的同时提高客户满意度，成为S企业迫切需要解决的关键问题。

本文提出了一种考虑交通路况的生鲜农产品末端配送路径优化方法，通过综合分析实际的交通状况、客户需求及配送成本因素，构建了一个多目标优化模型。首先，通过K近邻算法（KNN）对交通拥堵指数进行预测，并结合道路通行能力，以通行时间的形式对交通状况进行统一量化处理。该模型能够根据实时交通数据预测每条道路的通行时间，进而计算最短的配送路径。在此基础上，本文设计了基于产品新鲜度和配送时效性的客户满意度函数，结合固定成本、运输成本、货损成本、蓄冷成本和时间窗惩罚成本，最终构建了以客户满意度最大化和配送成本最小化为目标的多目标配送路径优化模型。

（2）在构建优化模型的过程中，本文对影响客户满意度的主要因素进行了详细分析。生鲜农产品的配送不仅需要考虑配送时间的最小化，还要保证产品在配送过程中的新鲜度，这直接关系到客户的最终体验。为此，本文引入了客户满意度函数，通过产品新鲜度和配送时效性来衡量客户的满意度水平。具体而言，产品新鲜度是通过产品在途时间和温控环境来确定的，配送时间越短，产品新鲜度越高；同时，配送时效性则通过准时送达率进行衡量，越接近客户预定的送达时间，客户满意度越高。

为了更好地控制成本，本文还对配送过程中产生的各种成本进行了量化分析。首先是固定成本，即车辆和配送设备的成本，这是配送中不可避免的部分。其次是运输成本，它直接与配送距离和时间相关，距离越长、时间越久，成本越高。此外，蓄冷成本与温控系统的工作时长密切相关，在高温环境下，需要更多的蓄冷能量来保持产品的新鲜度，这也会增加配送成本。最后，货损成本和时间窗惩罚成本是两个关键的成本因素。货损成本与产品的新鲜度和损坏率有关，时间窗惩罚成本则是在无法按时送达时产生的额外费用。这些成本在实际配送过程中对企业的整体利润影响重大，因此在优化模型中需要重点考虑。

在优化方法的选择上，本文设计了改进的NSGA-II（非支配排序遗传算法）来求解多目标优化问题。NSGA-II是一种多目标优化算法，能够在解决多个冲突目标时获得一组帕累托最优解。为了提高算法的寻优效率，本文引入了最邻近算法构造初始可行解，并设计了自适应交叉和变异算子，优化算法的搜索性能。通过最邻近算法，能够快速生成初始的配送路线，确保在算法初期能够找到较优解；而自适应交叉和变异算子则能提高搜索的多样性，避免陷入局部最优解，从而获得更好的全局最优解。

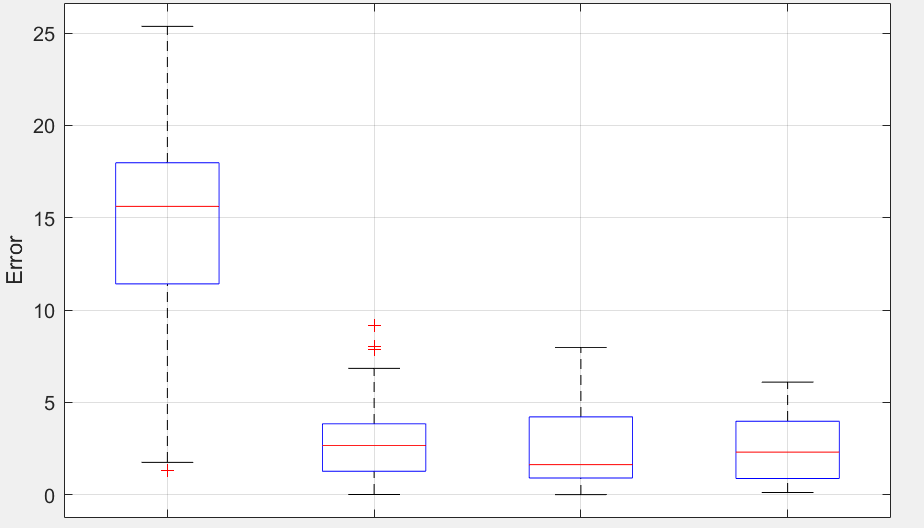
（3）为了验证本文所提出的优化方法的有效性，本文基于S企业末端配送的相关数据进行了实验分析。实验数据包括S企业的配送车辆数量、配送点位、交通状况等实际运营数据。通过将这些数据代入所构建的优化模型，本文分析了客户满意度与配送成本之间的关系，获得了一组帕累托最优解集。在帕累托解集中，不同解对应不同的客户满意度与配送成本组合，企业可以根据具体需求选择合适的配送方案。

实验结果表明，考虑交通路况的优化配送方案相比于S企业现有的配送方案，在多个维度上表现出了明显的优化效果。首先，在配送成本方面，改进方案相较于不考虑交通路况的初始方案，优化幅度达到20.38%，大大降低了配送的总体成本。其次，在客户满意度方面，改进方案相较于初始方案提高了11.81%，有效提高了客户的整体满意度。这表明，在考虑交通状况后，配送路径得到了显著优化，能够更好地平衡配送时间和成本，从而提升客户体验。

此外，本文还进行了交通状况和需求量变动的灵敏度分析。交通状况和需求量是影响末端配送路径的重要不确定因素，因此在实际配送过程中，必须针对这些变量进行充分的考虑。通过灵敏度分析，本文发现，当交通状况发生恶化时，配送成本会显著上升，而客户满意度则会有所下降。相反，当需求量增加时，合理的调度优化能够有效减少成本的上升幅度，并保持客户满意度相对稳定。这些结果为S企业制定更为科学合理的配送策略提供了重要参考，尤其是在应对交通高峰期和订单量波动时，企业可以根据不同的情况选择最优的配送路径，最大限度地降低成本并提高配送效率。

% MATLAB NSGA-II 算法优化末端配送路径示例

% 定义问题参数
num_customers = 20;  % 客户数量
num_vehicles = 5;    % 配送车辆数量
vehicle_capacity = 50; % 车辆容量

% 生成随机客户需求和位置
customer_demand = randi([5, 20], 1, num_customers);
customer_locations = rand(num_customers, 2) * 100;

% 定义配送车辆初始位置（假设配送中心位置为(50, 50)）
depot_location = [50, 50];

% 定义距离计算函数
function d = distance(loc1, loc2)
    d = sqrt(sum((loc1 - loc2).^2));
end

% 计算距离矩阵
distance_matrix = zeros(num_customers + 1, num_customers + 1);
for i = 1:num_customers
    for j = 1:num_customers
        distance_matrix(i, j) = distance(customer_locations(i, :), customer_locations(j, :));
    end
    distance_matrix(i, num_customers + 1) = distance(customer_locations(i, :), depot_location);
    distance_matrix(num_customers + 1, i) = distance(depot_location, customer_locations(i, :));
end

% 初始化NSGA-II算法参数
population_size = 50;    % 种群规模
max_generations = 100;   % 最大迭代次数
mutation_rate = 0.1;     % 变异率

% 定义适应度函数
function fitness = compute_fitness(route, customer_demand, vehicle_capacity)
    total_distance = 0;
    current_load = 0;
    
    for i = 1:length(route)
        if current_load + customer_demand(route(i)) <= vehicle_capacity
            current_load = current_load + customer_demand(route(i));
        else
            total_distance = total_distance + distance_matrix(route(i), num_customers + 1); % 返回配送中心
            current_load = customer_demand(route(i));  % 装载新的需求
        end
    end
    
    fitness = total_distance;
end

% 初始化种群并进行遗传算法迭代
for generation = 1:max_generations
    % 生成初始种群
    population = randi([1, num_customers], population_size, num_customers);
    
    % 计算适应度值
    fitness_values = zeros(1, population_size);
    for i = 1:population_size
        fitness_values(i) = compute_fitness(population(i, :), customer_demand, vehicle_capacity);
    end
    
    % 选择、交叉、变异等操作（此处省略详细代码）
    % ...
    
    % 更新种群
end

disp('优化后的最短配送路径为：');
disp(population(1, :)); % 输出最优路径