[移动通讯]【无线感知-P1】[从菲涅尔区模型到CSI模型-5]【The Riemann Mapping Theorem】

最新推荐文章于 2024-07-12 16:16:27 发布

明朝百晓生

最新推荐文章于 2024-07-12 16:16:27 发布

阅读量1k

点赞数 21

文章标签： python 开发语言

4AM_明朝百晓生

本文链接：https://blog.csdn.net/chengxf2/article/details/138195252

版权

前言：

mobius变换保角性证明一直困扰我很久.当看完黎曼映射定理以及结合MIT的数学证明

深刻的感触到数学之美，“知之深，情之切”。

黎曼映射（The Riemann Mapping）定理是复分析最深刻的定理之一，也是复变函数几何理论最基本、最重要的定理. 黎曼映射是 Mobius变换的核心定义之一

本节我们重点是搞清楚这个问题：

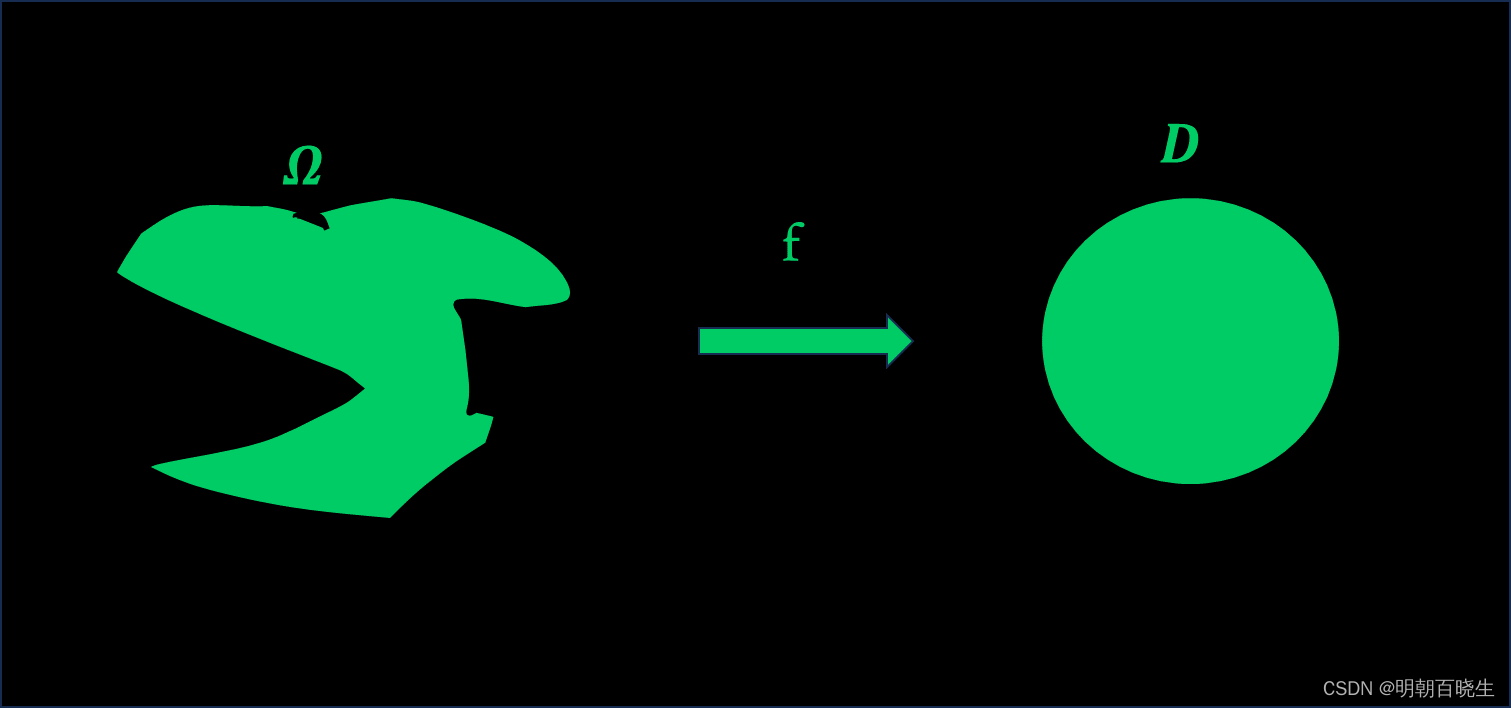
比如可以把一个随机的曲线映射成一个单位圆盘,直观上很难去想象.

黎曼映射定理
黎曼映射函数表示
黎曼映射例子
利用黎曼映射定理证明 Mobius 变换的保角性
黎曼映射应用

一黎曼映射定理

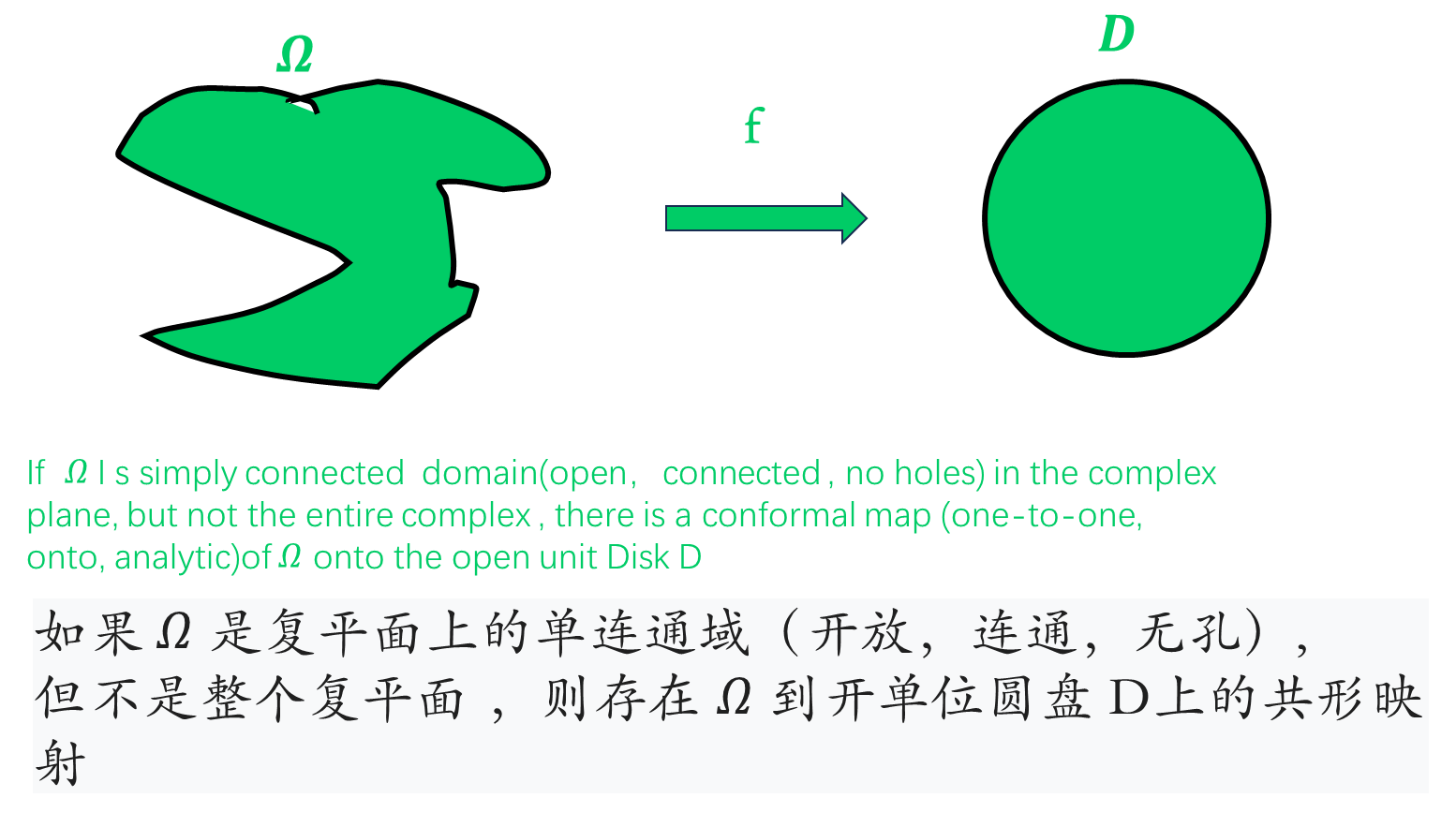
简单的说黎曼映射定理是存在性定理，存在一个共形映射把单连通域映射到圆盘.

1.1 Petra-Bonfert-Tayloy 是这么介绍

1.2 维基百科里面的简介

单连通[区]域（simply connected domain）是1993年公布的数学名词。

单连通域是直观上没有洞的平面区域的推广,即区域内任何一条简单闭曲线的内部没有不属于D的点。

二黎曼映射函数表示(Mobius 变换）

我们这里举一个例子：

因为存在共形映射，则假设单联通区域 $\Omega$ 中三个点 $z_0=0,z_1=1,z_2=\infty$ 通过mobius 变换 $w_1=1,w_2=i,w_3=-1$

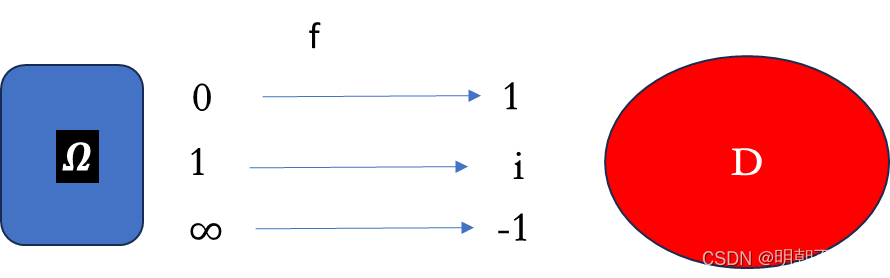
这个函数如何求解？

# -*- coding: utf-8 -*-
"""
Created on Sun Apr 28 15:48:31 2024

@author: chengxf2
"""

import numpy as np
import random
import matplotlib.pyplot as plt

def moubius_transformation(z):
    i = complex(0, 1)
    numerator =-z+i #分子
    denominator=z+i #分母
    
    result = (numerator/denominator)
    
    return result

    
    
def drawImage(z, w,bound):
    
    fig, (ax1, ax2) = plt.subplots(2)
    
    
    ax1.set_xlim(-bound,bound)
    ax1.set_ylim(-bound,bound)
    
    ax2.set_xlim(-1.5,1.5)
    ax2.set_ylim(-1.5,1.5)
    #print(z)
    # 第一个子图
    #plt.subplot(2, 1, 1)  # 表示2行1列的子图布局中的第1个位置
    z_x=  z[:, 0]
    z_y = z[:, 1]
    ax1.scatter(z_x,z_y,c='b')
    #plt.plot(x, y_sin)
    ax1.title.set_text("z")
    
    # 第一个子图
    plt.subplot(2, 1, 2)  # 表示2行1列的子图布局中的第1个位置
    w_x=  w[:, 0]
    w_y = w[:, 1]
    #print(w_x)
    ax2.scatter(w_x,w_y,c='r')
    ax2.title.set_text("w")

    # 显示图像
    plt.show()

def getData():
    N = int(1e5)
    ZList =[]
    WList =[]
    
    bound =1e3
    for i in range(N):
        # 随机生成复数的实部和虚部
        real_part = random.uniform(-bound, bound) # 实部在[-10, 10]范围内
        imaginary_part = random.uniform(0, bound)  # 虚部在[-10, 10]范围内
        # 生成的复数
        z = complex(real_part, imaginary_part)
        w = moubius_transformation(z)
        ZList.append([real_part,imaginary_part])
        WList.append([w.real, w.imag])
        
    drawImage(np.array(ZList), np.array(WList),bound)
        
getData()

三黎曼映射例子

基于上面的mobius transformation

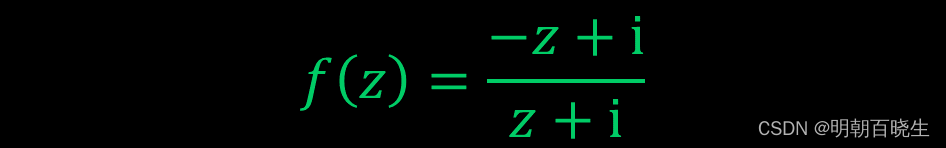
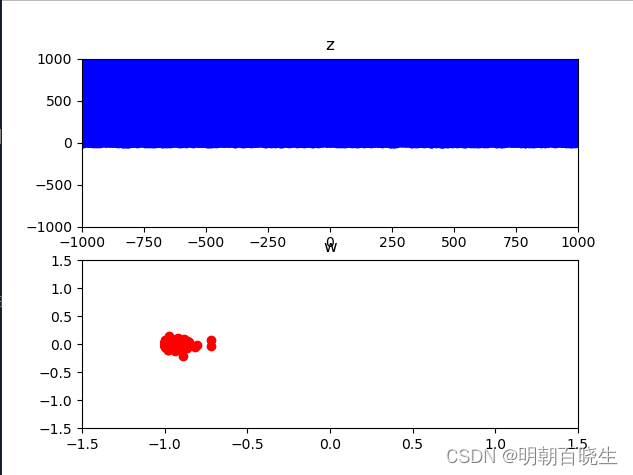
2.1 上半平面映射

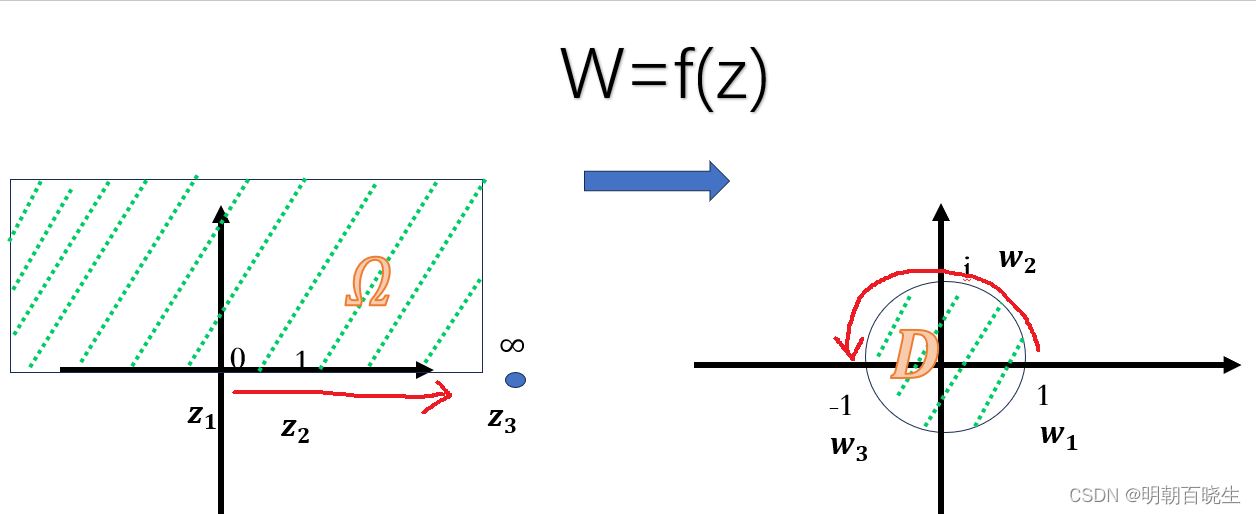
i.e $\Omega=\begin{Bmatrix} z: Im(z) >0 \end{Bmatrix}$ 为上半平面，我们发现通过Mobius transformation 函数f变换

后可以得到一个单位圆盘.

1 通过0,1, $\infty$ 直线（real axis）映射成了一个单位圆

2 原来直线导向为 $z_1->z_2->z_3$ , 对应单位圆上的导向 $w_1->w_2->w_3$

我们可以带入z=-1

$f(z=-1)=\frac{1+i}{-1+i}=-i$

3.2 第一象限的Mobius 变换

使用上面的mobius 映射 $f(z)=\frac{-z+i}{z+i}$

但是约束条件发生变化， $\Omega$ 被限制在第一象限内.则经过mobius 变化后对应为一个半圆.

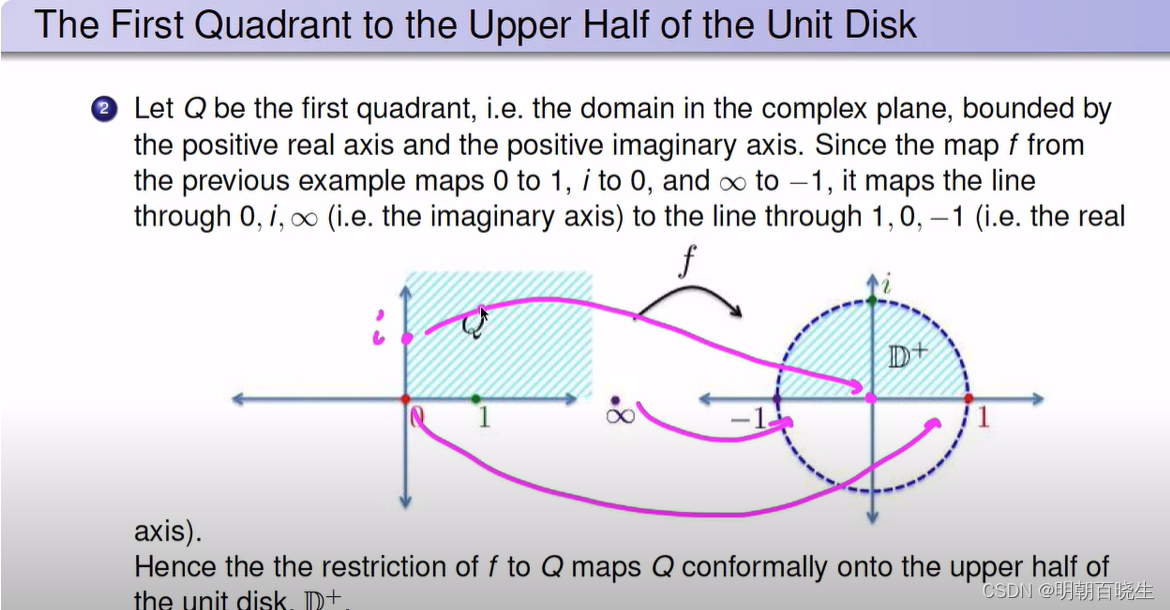
设Q 为第一象限，其复平面被约束再正实坐实轴以及正虚轴,对应的映射为一个半圆.

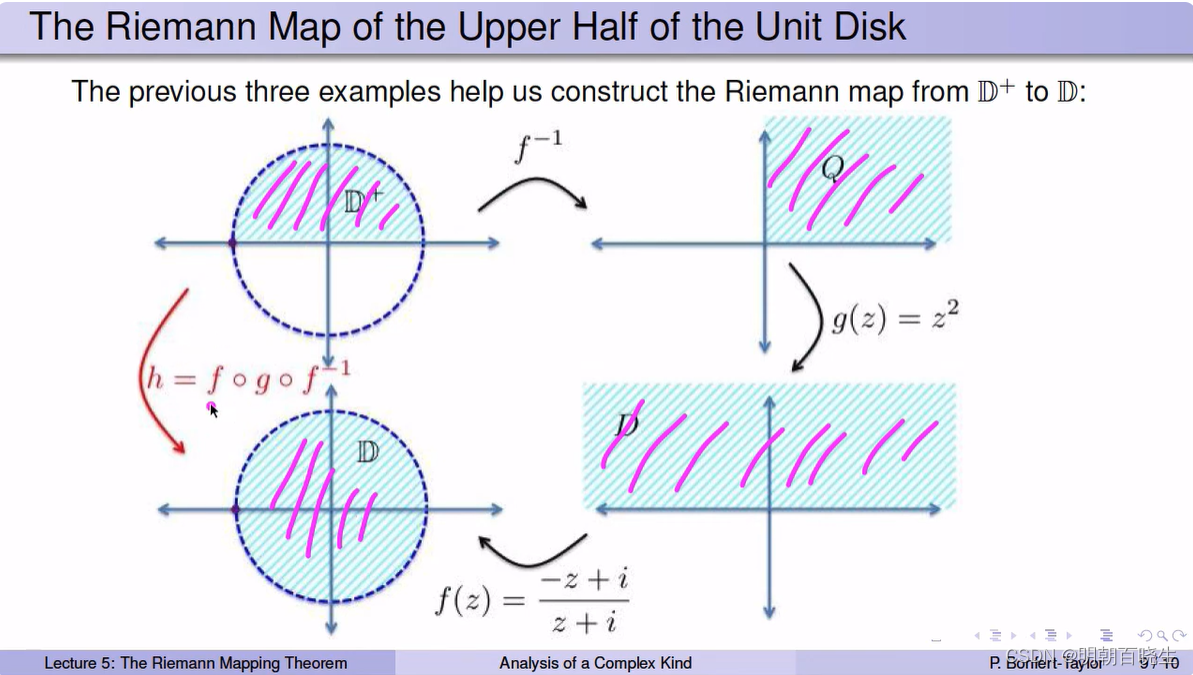
3.3 我们可以通过下面几个变换还原出原来的集合形状

四利用黎曼映射定理证明 Mobius 变换的保角性

我们需要证明经过Mobius transformation 后，两张几何图片的夹角相同

$\alpha =\beta$

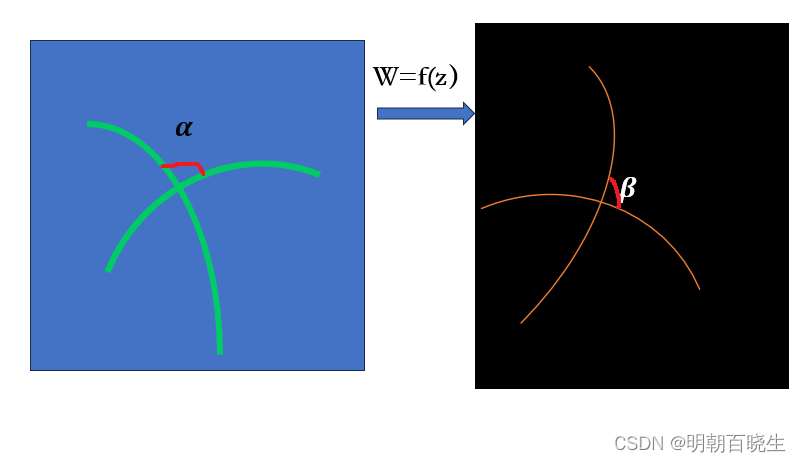
证明：

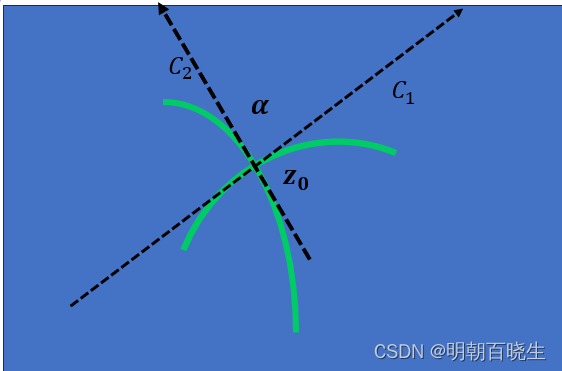
1：以两条曲线的交点 $z_0$ 为中心,分别做两条曲线的切线 $c_1,c_2$ ，

则 $c_1,c_2$ 之间的夹角就是原来曲线的夹角

2：以交点 $z_0$ 为圆心,半径为r 做一个圆跟两条切线相交于 $z_1,z_2$

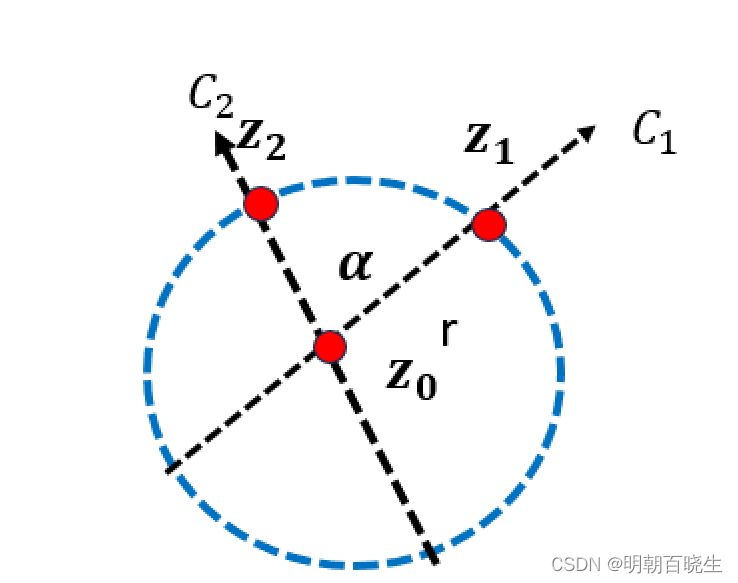
设

$Z_1-Z_0= r e^{j\theta_1}$

$Z_2-Z_0= r e^{j\theta_2}$

则

3 角度计算

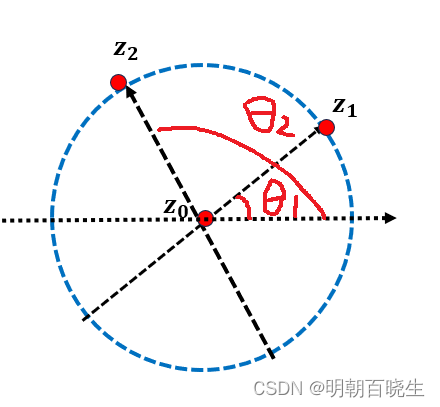
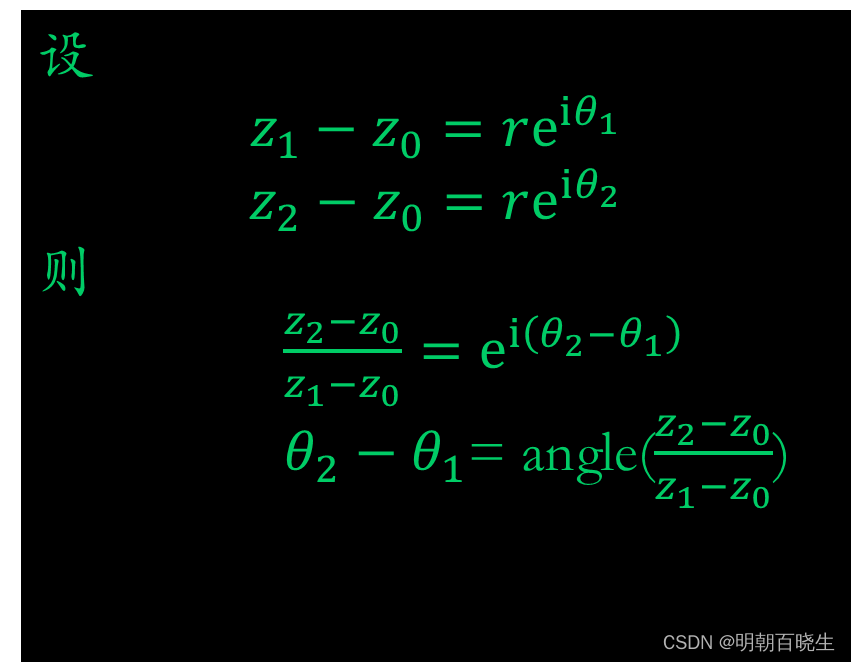
则

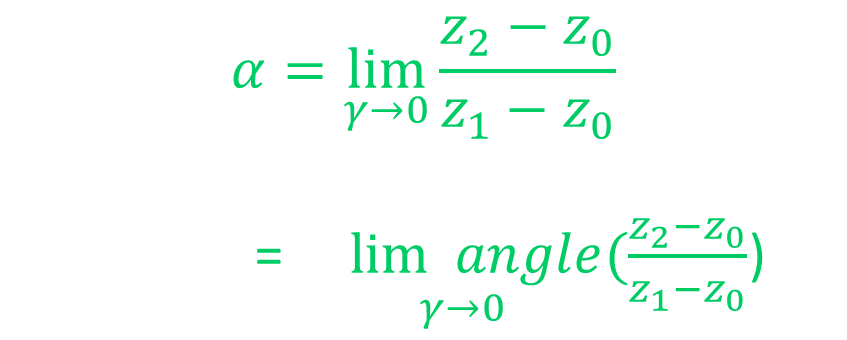
4 利用黎曼映射定理，存在一个映射 one-to-one confromal mapping

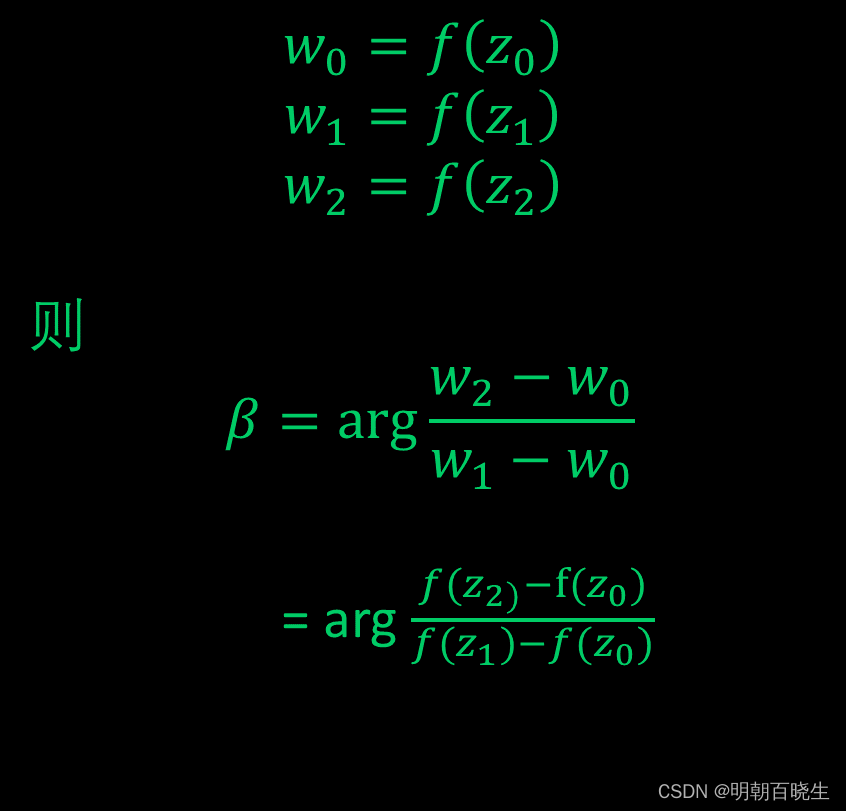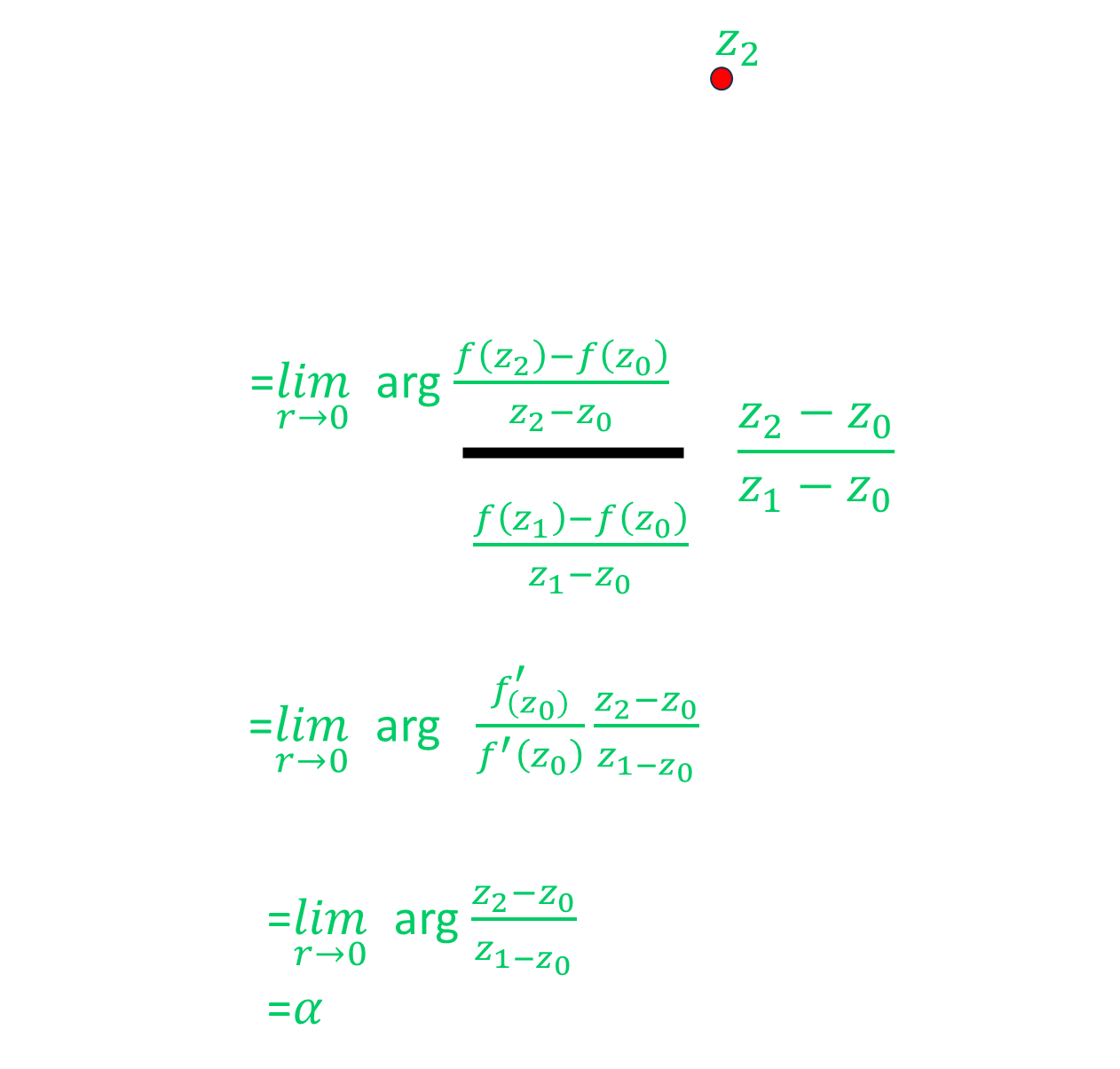
五黎曼映射的应用

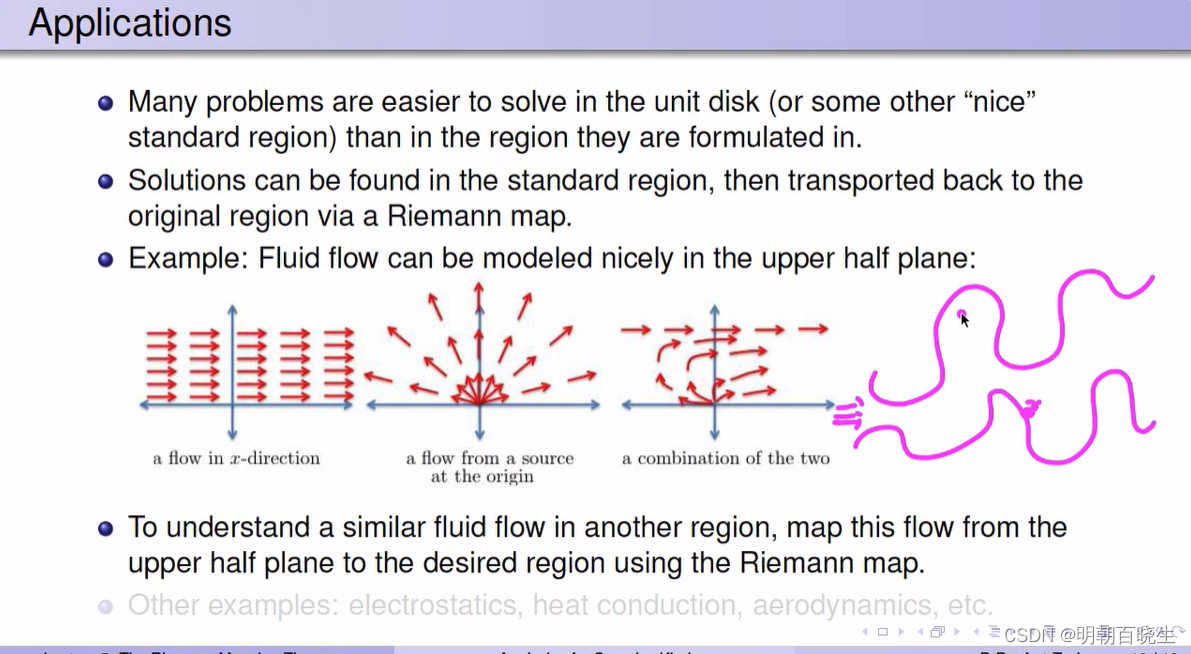流体流动可以在上半平面中很好地建模。
了解另一个区域的类似流体流动，将这个流从上半平面映射到,使用黎曼映射的期望区域。

我们做6G智能感知的时候，基于CSI RESnel 建模可以理解在一个有噪声的域中建模

映射到一个无噪声的域中，在无噪声的环境中分析模型，然后通过Mobius 反演，平移，膨胀

等操作还原出原域的几何形状.

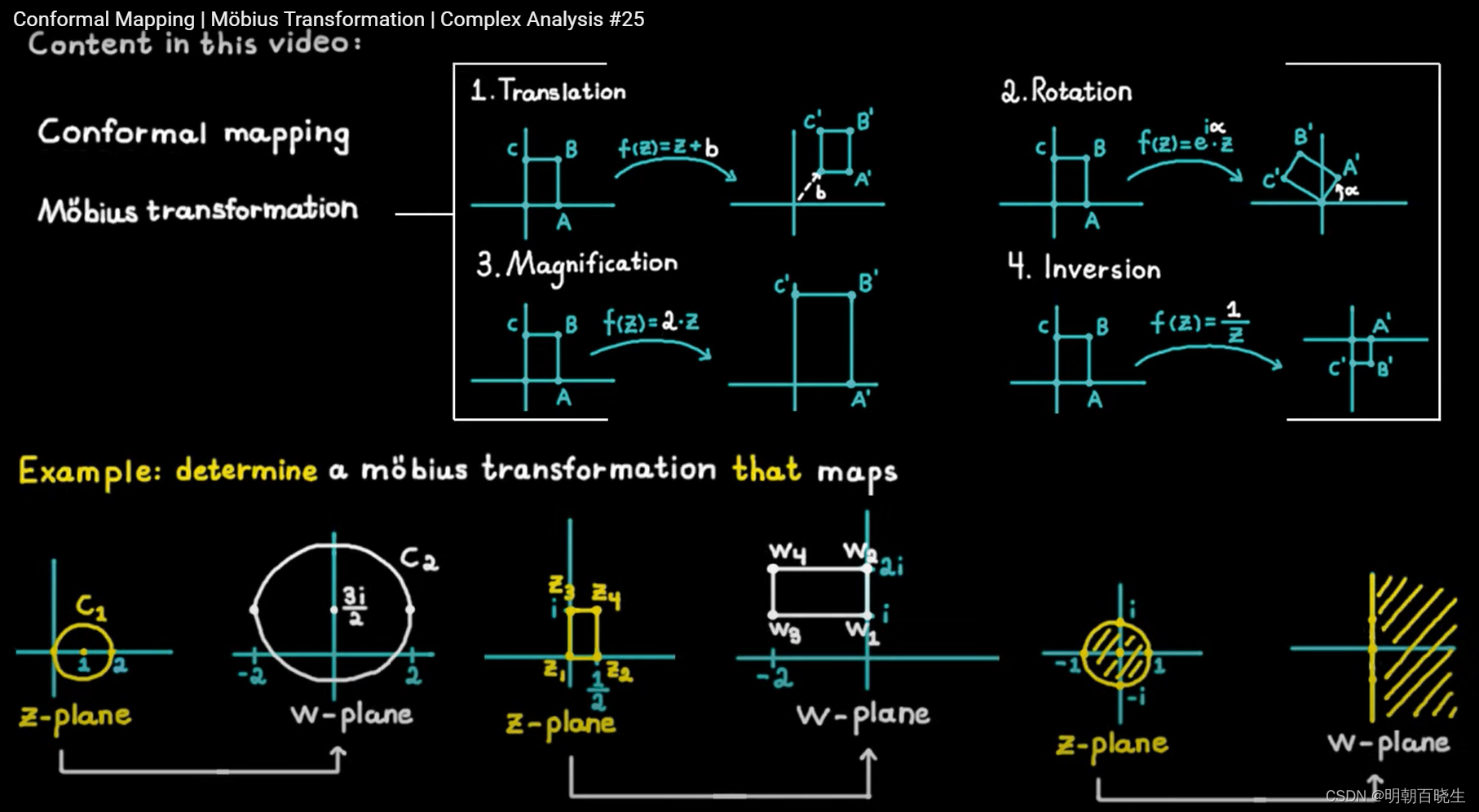
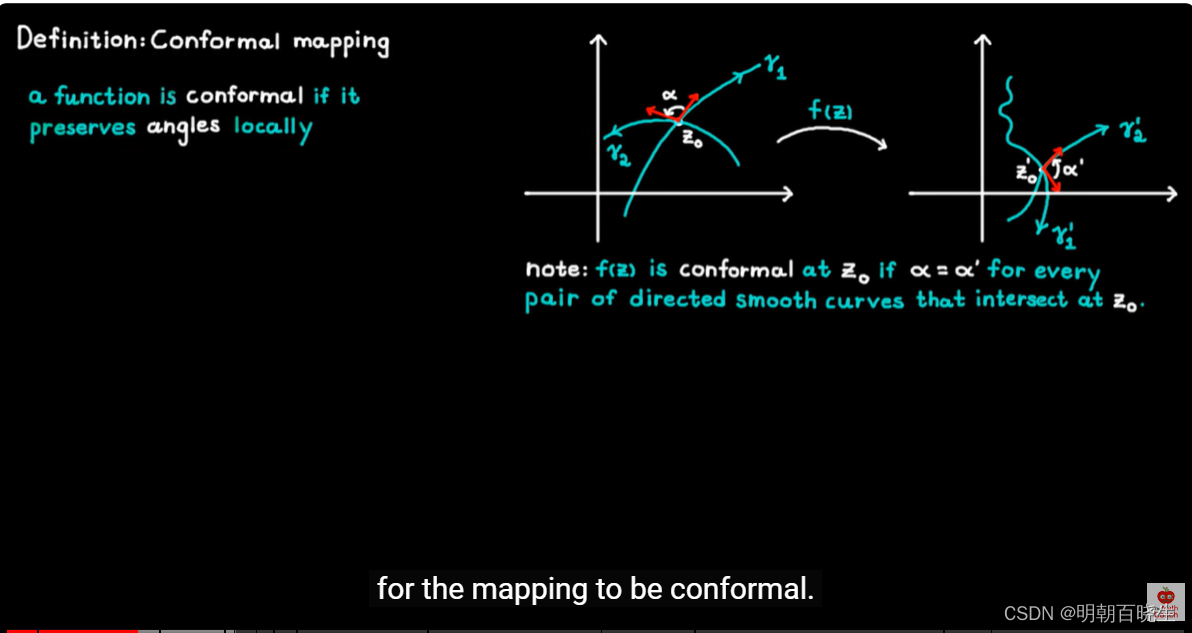
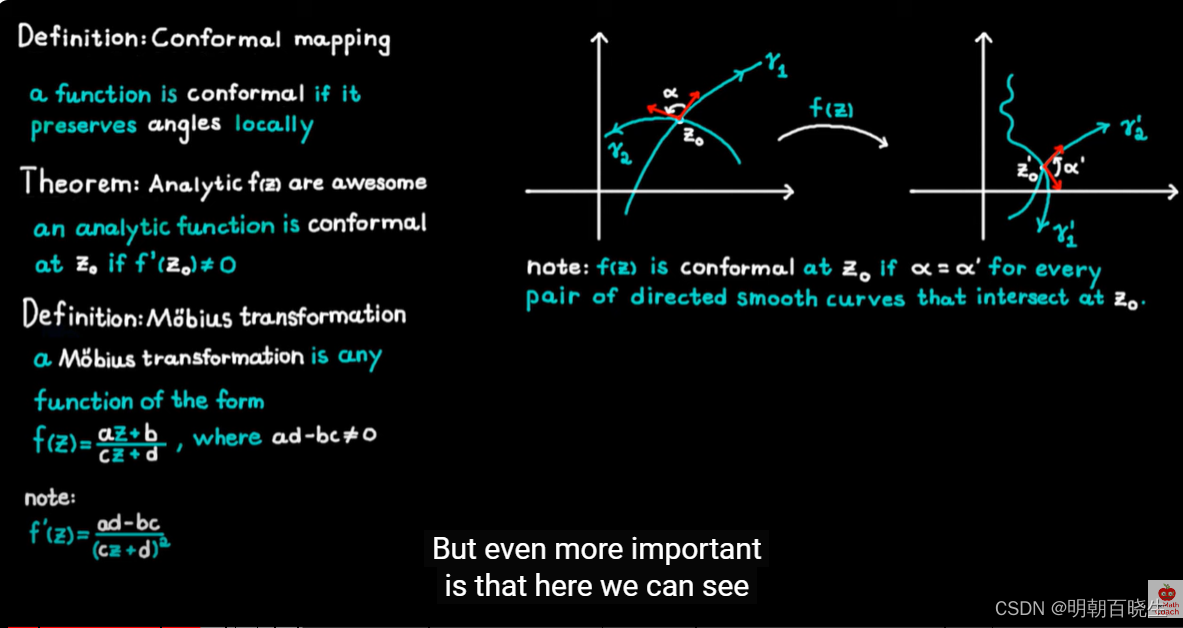
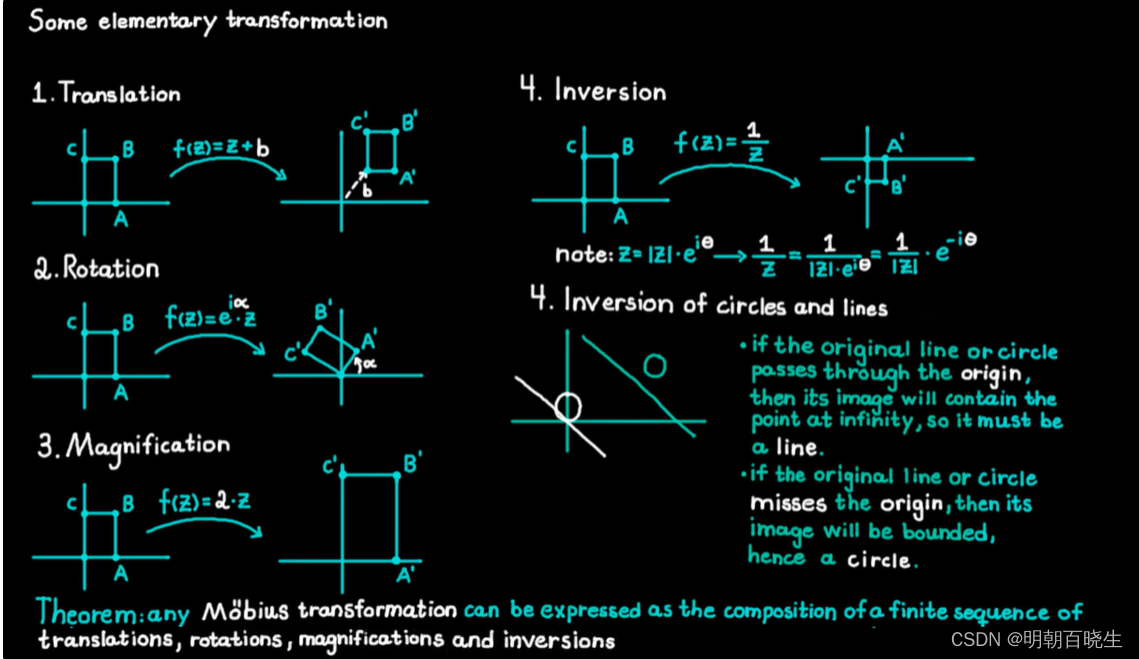
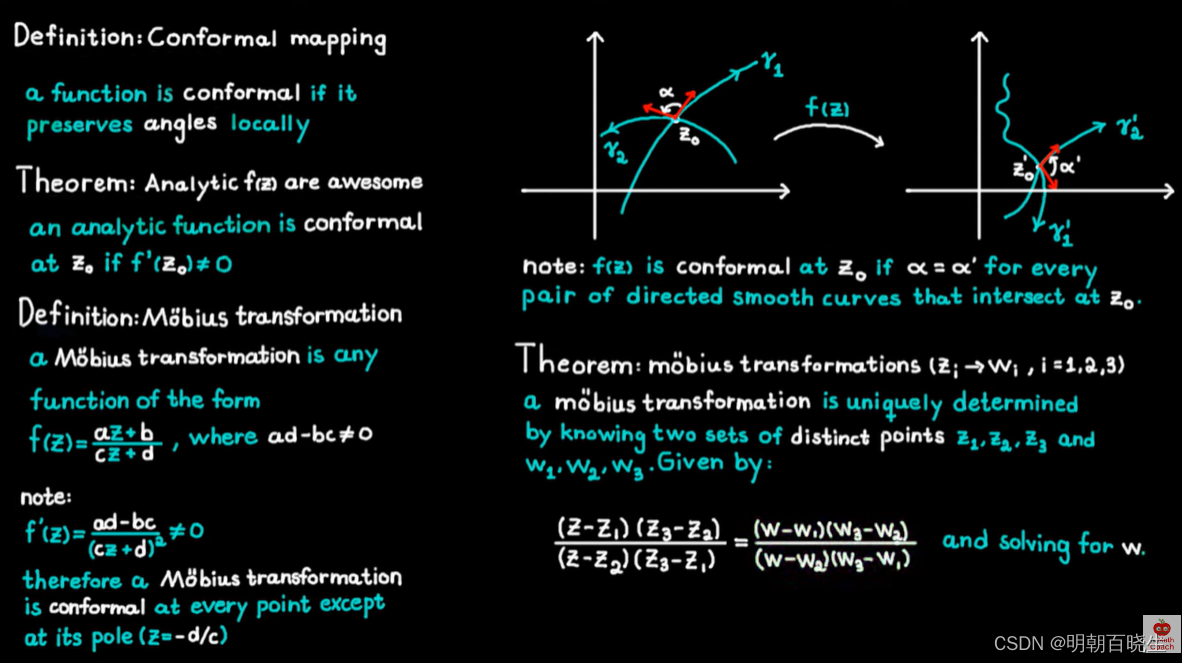
一些其它课程例子

单连通区域_百度百科

https://www.youtube.com/watch?v=48aerHs9wL0&t=1165s

黎曼映射定理_百度百科

共形映射_百度百科

保角变换_百度百科

明朝百晓生

关注

21
点赞
踩
24

收藏

觉得还不错? 一键收藏
0
评论
[移动通讯]【无线感知-P1】[从菲涅尔区模型到CSI模型-5]【The Riemann Mapping Theorem】

黎曼映射（The Riemann Mapping）定理是复分析最深刻的定理之一，也是复变函数几何理论最基本、最重要的定理. 黎曼映射是 Mobius变换的核心定义之一。单连通域是直观上没有洞的平面区域的推广,即区域内任何一条简单闭曲线的内部没有不属于D的点。映射到一个无噪声的域中，在无噪声的环境中分析模型，然后通过Mobius 反演，平移，膨胀。了解另一个区域的类似流体流动，将这个流从上半平面映射到,使用黎曼映射的期望区域。被限制在第一象限内.则经过mobius 变化后对应为一个半圆.
复制链接

扫一扫