1. 渲染全屏矩形 [-1,1],是由两个三角形组成。
也可以使用一个三角形,它和屏幕剪裁后便是[-1,1]的矩形。 三角形为:const float2 vertices[] = { float2(0, 2), float2(3, -1), float2(-3, -1) };
2.一位(8bit)表示256,看看Lbuffer表示的电光源距离,CPU做剪裁注意吧
3.
平移矩阵的逆矩阵可以直接将平移参数取负.
缩放矩阵的逆矩阵就是将对角线上的三个缩放参数取自身的倒数。
旋转矩阵的逆矩阵可以将旋转的角度参数取负,表示再转过相反的角度。
5.
转置矩阵:一个矩阵的转置矩阵就是将这个矩阵的行列交换。
逆矩阵:一个矩阵乘以它的逆矩阵得到单位矩阵。
正交矩阵:若一个矩阵的转置矩阵就是它的逆矩阵,那么这个矩阵就是正交矩阵。
旋转矩阵是正交矩阵
使用矩阵乘法并把(纵列)向量当作n×1矩阵,点积还可以写为: a ·b = abT. 由a和b的点乘变换为a和b的转置的叉乘。n x 1矩阵和1 x n矩阵叉乘结果还是标量。
6.法向量变换受所在三角形影响,变换后的三角形可能已经形变,在变换到view空间不能只乘以matrixWV,要乘以matrixWV的转置再逆。当然,像平面这种由法线构成的结构也是如此的!
物体三角形本地空间:物体的本地坐标系。 法线是根据平面计算出来的。
7. 凹凸纹理转法向量
// Sample the pixel in the bump map.
bumpMap = normalMapTexture.Sample(SampleType, input.tex);
// Expand the range of the normal value from (0, +1) to (-1, +1).
bumpMap = (bumpMap * 2.0f) - 1.0f;
// Calculate the normal from the data in the bump map.
bumpNormal = input.normal + bumpMap.x * input.tangent + bumpMap.y * input.binormal;
// Normalize the resulting bump normal.
bumpNormal = normalize(bumpNormal);
8. 空间位置对纹理坐标造成的影响,而进行的纹理坐标改变计算,要转换到切向空间进行计算。
9. 三角形的重心:三角形三边中点的连线。具有很多性质。图形渲染选择三角形内部任意一点,重心一定在三角形内部。不知道还常用来做什么?
10. 为什么不在VS做透视投影的除w?
VS中: 如果w为负,xyz/w,会使xyz的符号取反。 w为负, 小于nearplane的被裁掉,会把整个三角形都弄乱
VS后PS前得clip:判-w < x < w 会错误的剪裁
PS中:除以w是pixel级别剔除
11. 透视纹理影射:uv方向的插值。 uv在平面空间和1/z是线性关系,uv*1/z进行插值,然后再除以1/z得到正确的uv。
12.D3DXMatrixPerspectiveFovLH() 成像在中心
D3DXMatrixPerspectiveOffCenterLH成像可以有偏移
13.TBN矩阵
T和B为U和V方向。
T和B是该三角形所在的平面,N垂直于三角形平面。
我觉得这样理解:T和B的值为纹理坐标UV在三角形本地空间坐标系下的值
三角形本地空间坐标系 那有这样的坐标系,其实就是模型的本地空间坐标系
积累中,未完待续...








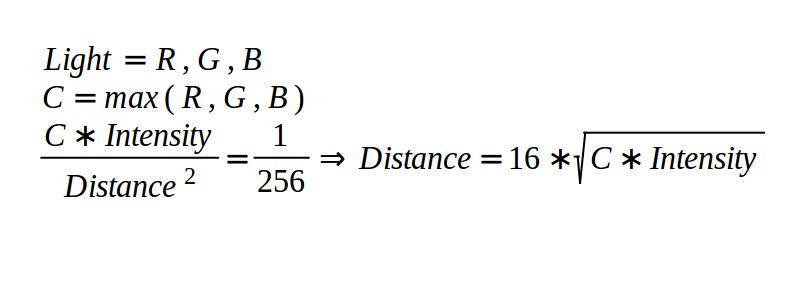














 650
650

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








