在三维空间中,旋转变换是最基本的变换类型之一,有多种描述方式,如Euler角、旋转矩阵、旋转轴/旋转角度、四元数等。本文将介绍各种描述方式以及它们之间的转换。
1. 旋转矩阵
用一个3阶正交矩阵来表示旋转变换,是一种最常用的表示方法。容易证明,3阶正交阵的自由度为3。注意,它的行列式必须等于1,当等于-1的时候相当于还做了一个镜像变换。
2. Euler角
根据Euler定理,在三维空间中,任意一种旋转变换都可以归结为若干个沿着坐标轴旋转的组合,组合的个数不超过三个并且两个相邻的旋转必须沿着不同的坐标轴。因此,可以用三个沿着坐标轴旋转的角度来表示一个变换,称为Euler角。旋转变换是不可交换的,根据旋转顺序的不同,有12种表示方式,分别为:XYZ、XZY、XYX、XZX、YXZ、YZX、YXY、YZY、ZXY、ZYX、ZXZ、ZYZ,可以自由选择其中的一种。对于同一个变换,旋转顺序不同,Euler角也不同,在指定Euler角时应当首先约定旋转顺序。
2.1 Euler角 转化为 旋转矩阵
不妨设先绕Z轴旋转γ,再绕Y轴旋转β,最后绕X轴旋转α,即旋转顺序为XYZ,旋转矩阵
3. 旋转轴/旋转角度
用旋转轴的方向向量n和旋转角度θ来表示一个旋转,其中
θ>0表示逆时针旋转。
3.1 旋转轴/旋转角度 转化为 旋转矩阵
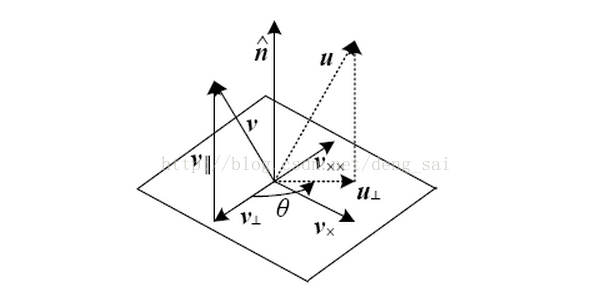
设v是任意一个向量,定义
如下图所示
这样,我们建立了一个直角坐标系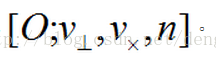
设u为v绕轴旋转后得到的向量,则有
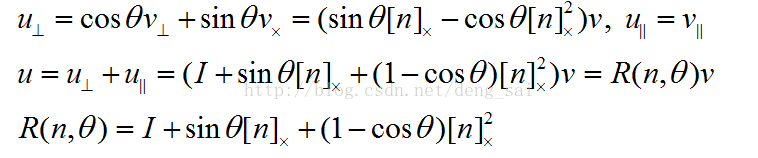
4. 单位四元数(Unit quaternions)
四元数由Hamilton于1843年提出,实际上是在四维向量集合上定义了通常的向量加法和新的乘法运算,从而形成了一个环。
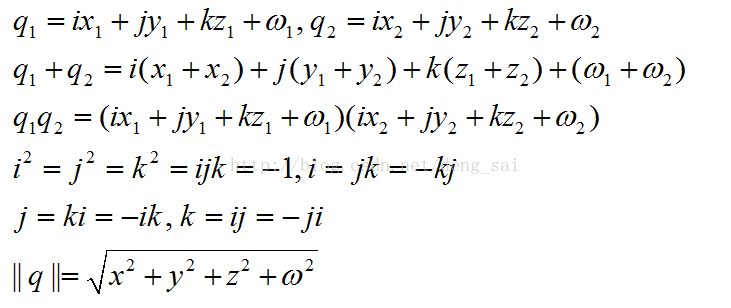
q称为单位四元数,如果||q||=1。一个单位四元数可以表示三维旋转。用单位四元数表示旋转可以保持一个光滑移动的相机的轨迹,适合动画生成。
4.1 旋转轴/旋转角度 转化为 单位四元数
根据旋转轴n和旋转角度θ,得到单位四元数q
4.2 单位四元数 转化为 旋转轴/旋转角度
4.3 单位四元数 转化为 旋转矩阵
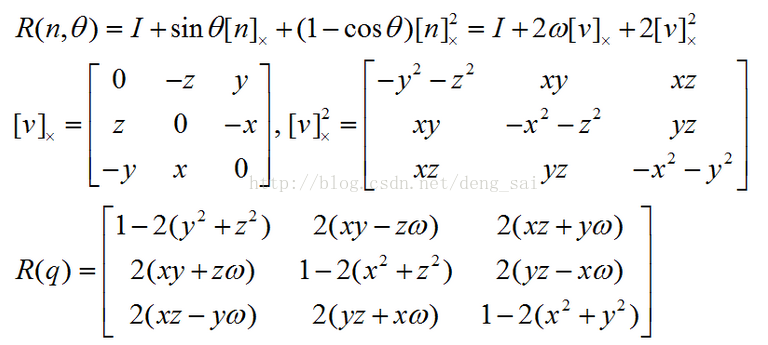
4.4 四元数的性质
定义四元数的逆、乘法和除法,如下所示
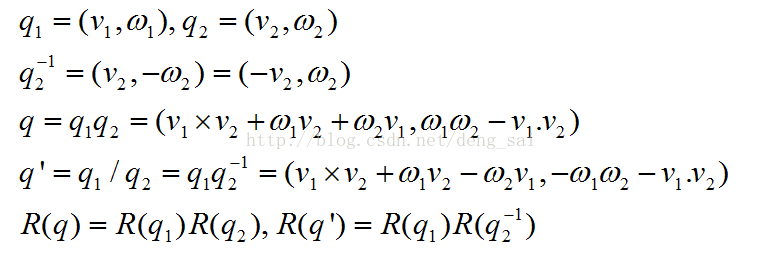
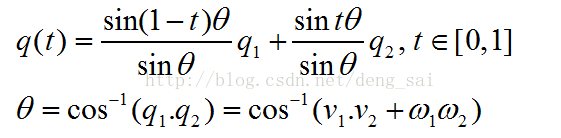








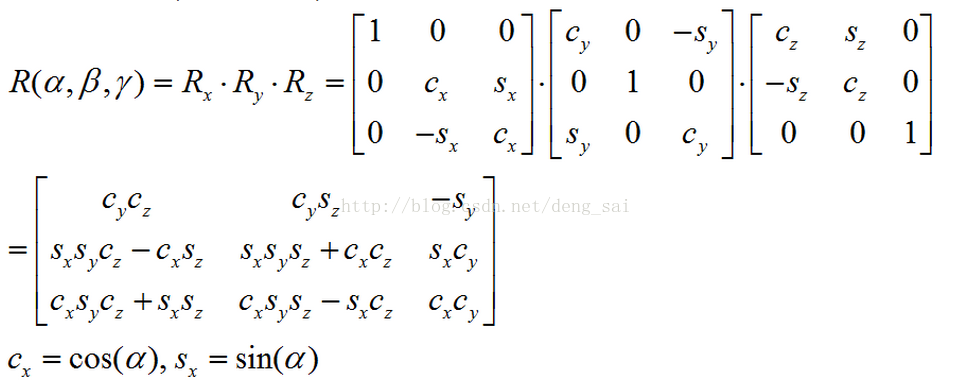
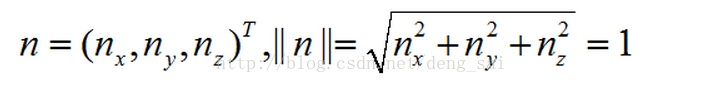
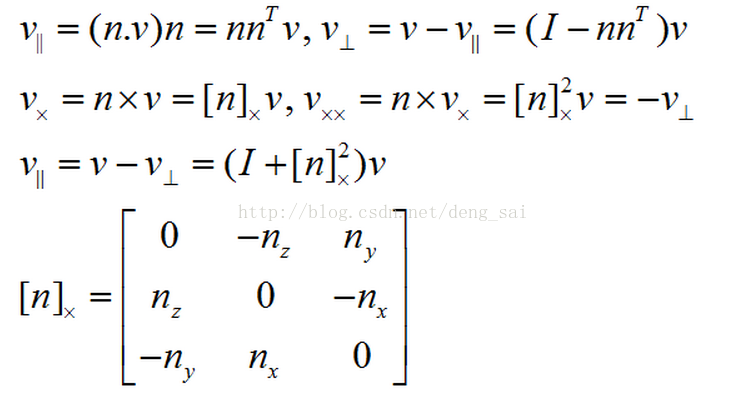
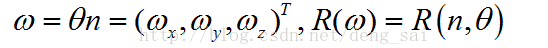
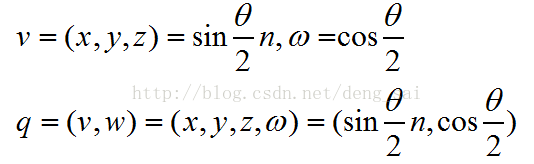
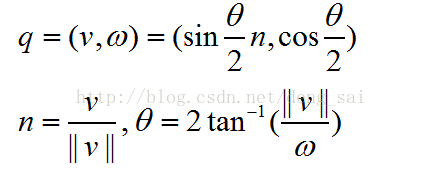















 550
550

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








