三维旋转矩阵
二维旋转

先考虑二维的旋转,根据三角函数的关系,可以得到:
{
x
′
=
∣
O
P
∣
⋅
cos
(
α
+
β
)
=
∣
O
P
∣
⋅
(
cos
α
⋅
cos
β
−
sin
α
⋅
sin
β
)
=
x
⋅
cos
β
−
y
⋅
sin
β
y
′
=
∣
O
P
∣
⋅
sin
(
α
+
β
)
=
∣
O
P
∣
⋅
(
cos
α
⋅
sin
β
+
sin
α
⋅
cos
β
)
=
x
⋅
sin
β
+
y
⋅
cos
β
\begin{cases}x'=\begin{vmatrix}OP\end{vmatrix}\cdot\cos(\alpha+\beta)=\begin{vmatrix}OP\end{vmatrix}\cdot(\cos\alpha\cdot\cos\beta-\sin\alpha\cdot\sin\beta)=x\cdot\cos\beta-y\cdot\sin\beta\\y'=\begin{vmatrix}OP\end{vmatrix}\cdot\sin(\alpha+\beta)=\begin{vmatrix}OP\end{vmatrix}\cdot(\cos\alpha\cdot\sin\beta+\sin\alpha\cdot\cos\beta)=x\cdot\sin\beta+y\cdot\cos\beta\end{cases}
{x′=
OP
⋅cos(α+β)=
OP
⋅(cosα⋅cosβ−sinα⋅sinβ)=x⋅cosβ−y⋅sinβy′=
OP
⋅sin(α+β)=
OP
⋅(cosα⋅sinβ+sinα⋅cosβ)=x⋅sinβ+y⋅cosβ
用矩阵形式表示:
[
x
′
y
′
]
=
[
cos
β
−
sin
β
sin
β
cos
β
]
.
[
x
y
]
\begin{bmatrix}x^{'}\\y^{'}\end{bmatrix}=\begin{bmatrix}\cos\beta&-\sin\beta\\\sin\beta&\cos\beta\end{bmatrix}.\begin{bmatrix}x\\y\end{bmatrix}
[x′y′]=[cosβsinβ−sinβcosβ].[xy]
旋转矩阵即为:
[
cos
β
−
sin
β
sin
β
cos
β
]
\begin{bmatrix}\cos\beta&-\sin\beta\\\sin\beta&\cos\beta\end{bmatrix}
[cosβsinβ−sinβcosβ]
三维旋转
借助二维旋转矩阵,可以推广到三维的情况中,这里我们考虑 X , Y , Z X,Y,Z X,Y,Z的情况(暂时只考虑了正方向的转动,逆方向是正向旋转矩阵的逆矩阵,由于旋转矩阵是正交阵,所以逆矩阵是转置矩阵)
1. 绕 z z z轴

绕
z
z
z轴比较简单,直接增加一个
z
z
z轴,坐标
z
z
z不变即可:
{
x
′
=
x
⋅
cos
β
−
y
⋅
sin
β
y
′
=
x
⋅
sin
β
+
y
⋅
cos
β
z
′
=
z
[
x
′
y
′
z
′
]
=
[
cos
β
−
sin
β
0
sin
β
cos
β
0
0
0
1
]
⋅
[
x
y
z
]
\begin{gathered} \begin{cases}x^{'}=x\cdot\cos\beta-y\cdot\sin\beta\\y^{'}=x\cdot\sin\beta+y\cdot\cos\beta\\z^{'}=z\end{cases} \\ \begin{bmatrix}x^{'}\\y^{'}\\z^{'}\end{bmatrix}=\begin{bmatrix}{\cos\beta}&-\sin\beta&0\\\sin\beta&\cos\beta&0\\0&0&1\end{bmatrix}\cdot\begin{bmatrix}x\\y\\z\end{bmatrix} \end{gathered}
⎩
⎨
⎧x′=x⋅cosβ−y⋅sinβy′=x⋅sinβ+y⋅cosβz′=z
x′y′z′
=
cosβsinβ0−sinβcosβ0001
⋅
xyz
2. 绕 y y y轴
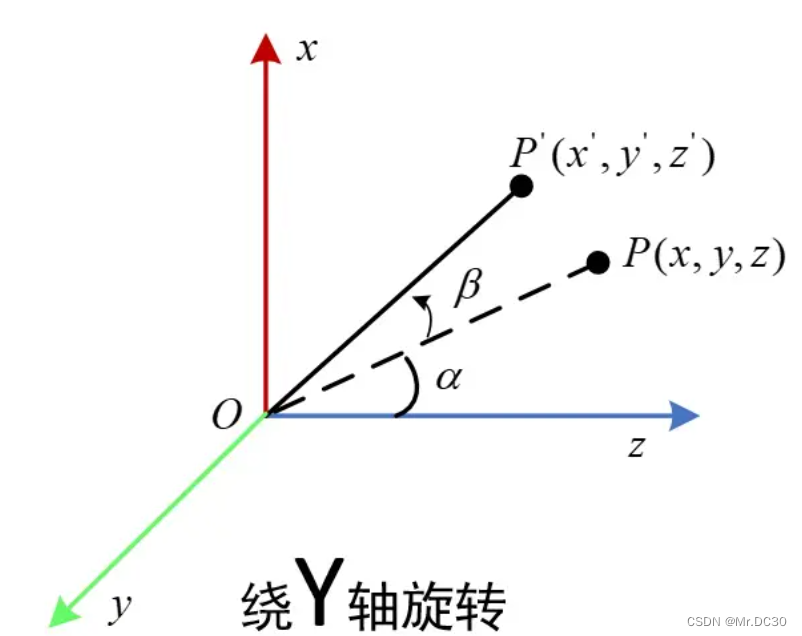
同绕
z
z
z轴类似,让
y
y
y不变即可;
{
x
′
=
x
⋅
cos
β
+
z
⋅
sin
β
y
′
=
y
z
′
=
−
x
⋅
sin
β
+
z
⋅
cos
β
[
x
′
y
′
z
′
]
=
[
cos
β
0
sin
β
0
1
0
−
sin
β
0
cos
β
]
⋅
[
x
y
z
]
\begin{gathered} \begin{cases}x^{'}=x\cdot\cos\beta+z\cdot\sin\beta\\y^{'}=y\\z^{'}=-x\cdot\sin\beta+ z\cdot\cos\beta\end{cases} \\ \begin{bmatrix}x^{'}\\y^{'}\\z^{'}\end{bmatrix}=\begin{bmatrix}{\cos\beta}&0&\sin\beta\\0&1&0\\-\sin\beta&0&\cos\beta\end{bmatrix}\cdot\begin{bmatrix}x\\y\\z\end{bmatrix} \end{gathered}
⎩
⎨
⎧x′=x⋅cosβ+z⋅sinβy′=yz′=−x⋅sinβ+z⋅cosβ
x′y′z′
=
cosβ0−sinβ010sinβ0cosβ
⋅
xyz
3. 绕 x x x轴

{
y
′
=
y
⋅
cos
β
−
z
⋅
sin
β
z
′
=
y
⋅
sin
β
+
z
⋅
cos
β
x
′
=
x
[
y
′
z
′
x
′
]
=
[
cos
β
−
sin
β
0
sin
β
cos
β
0
0
0
1
]
⋅
[
y
z
x
]
⇒
[
x
′
y
′
z
′
]
=
[
1
0
0
0
cos
β
−
sin
β
0
sin
β
cos
β
]
⋅
[
x
y
z
]
\begin{aligned} &\begin{cases}y^{'}=y\cdot\cos\beta-z\cdot\sin\beta\\z^{'}=y\cdot\sin\beta+z\cdot\cos\beta\\x^{'}=x\end{cases} \\ &\begin{bmatrix}y^{'}\\z^{'}\\x^{'}\end{bmatrix}=\begin{bmatrix}\cos\beta&-\sin\beta&0\\\sin\beta&\cos\beta&0\\0&0&1\end{bmatrix}\cdot\begin{bmatrix}y\\z\\x\end{bmatrix}\Rightarrow\begin{bmatrix}x^{'}\\y^{'}\\z^{'}\end{bmatrix}=\begin{bmatrix}1&0&0\\0&\cos\beta&-\sin\beta\\0&\sin\beta&\cos\beta\end{bmatrix}\cdot\begin{bmatrix}x\\y\\z\end{bmatrix} \end{aligned}
⎩
⎨
⎧y′=y⋅cosβ−z⋅sinβz′=y⋅sinβ+z⋅cosβx′=x
y′z′x′
=
cosβsinβ0−sinβcosβ0001
⋅
yzx
⇒
x′y′z′
=
1000cosβsinβ0−sinβcosβ
⋅
xyz








 本文详细解释了二维旋转矩阵的原理,并扩展到三维空间,介绍了绕z、y、x轴旋转时的矩阵变换,强调了正交性和逆矩阵的关系。
本文详细解释了二维旋转矩阵的原理,并扩展到三维空间,介绍了绕z、y、x轴旋转时的矩阵变换,强调了正交性和逆矩阵的关系。
















 4327
4327

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








