图像压缩编码——香农/哈夫曼编码

最新推荐文章于 2023-06-08 13:44:35 发布

didjjdj

最新推荐文章于 2023-06-08 13:44:35 发布

阅读量851

点赞数

本文链接：https://blog.csdn.net/didjjdj/article/details/115446869

版权

本文介绍了Python矩阵的基本运算，并深入讲解了梯度下降法，包括梯度的定义、微分的定义以及梯度下降法在机器学习中的应用。通过手动和Excel求解梯度下降法的例子，展示了如何寻找目标函数的最小值。此外，文章还讨论了线性回归中的代价函数及其梯度，并给出了相应的代码实现和图像展示。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、Python矩阵基本运算学习

在这里插入图片描述

二、梯度下降法

梯度的定义

梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

微分的定义

微分在数学中的定义：由函数B=f(A)，得到A、B两个数集，在A中当dx靠近自己时，函数在dx处的极限叫作函数在dx处的微分，微分的中心思想是无穷分割。

梯度下降法的定义

梯度下降在机器学习中应用十分的广泛，不论是在线性回归还是Logistic回归中，它的主要目的是通过迭代找到目标函数的最小值，或者收敛到最小值。

梯度算法手工求解

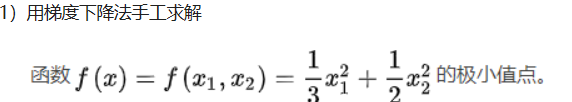
在这里插入图片描述

Excel梯度下降法求解

求:z=2(x-1)^2 + y^2的近似根
在这里插入图片描述
迭代到第1000步，极值一直不出来
修改学习率为0.15，极值出来了为（0，0）

线性回归求解

在这里插入图片描述
定义一个代价函数
代码如下

#导入bumpy包
from numpy import *
#定义别名
import numpy as np
# 定义数据集的大小 即20个数据点
m = 20
# x的坐标以及对应的矩阵
X0 = ones((m, 1))  # 生成一个m行1列的向量，其值全是1
X1 = arange(1, m+1).reshape(m, 1)  # 生成一个m行1列的向量，也就是x1，

最低0.47元/天解锁文章