ORB-SLAM3单目初始化,地图的初始化

源代码ORB_SLAM3（https://github.com/UZ-SLAMLab/ORB_SLAM3）
https://mp.weixin.qq.com/s/vdnQfHoCIS5XZvYz2mCGNA

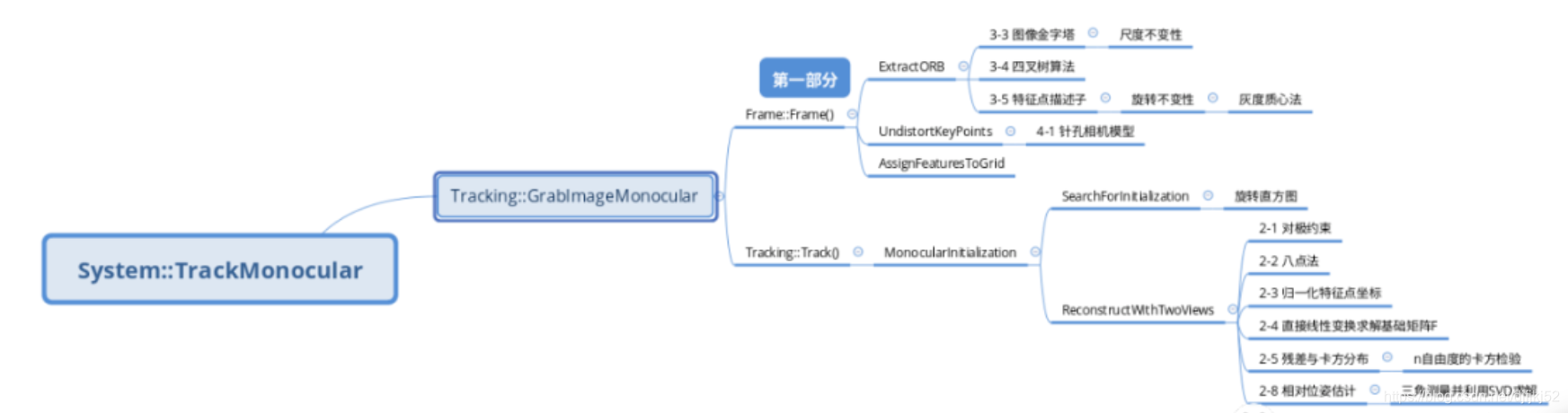
TrackMonocular是ORBSLAM单目视觉SLAM的追踪器接口，因此从这里入手。其中GrabImageMonocular下⾯有2个主要的函数：Frame::Frame()和Tracking::Track()。我会按照下⾯的框架流程来分解单⽬初始化过程，以便对整个流程有⽐较清晰的认识。

记录了Frame::Frame()

1.Frame::Frame()
1)作用
主要完成工作是特征点提取，涉及到的知识点其实很多，包括图像金字塔、特征点均匀化、四叉树算法分发特征点、特征点方向计算等等
2)主要的三个函数 ExtractORB UndistortKeyPoints AssignFeaturesToGrid
Frame()中其实调用的是ORBextractor::operator()，是一个重载操作符函数，此系列笔记主要针对重点理论如何落实到代码上，不涉及编程技巧，因此不讨论该函数的原理和实现，直接深入，探寻本质。

对这个单目图像进行提取特征点 Frame::ExtractORB

用OpenCV的矫正函数、内参对提取到的特征点进行矫正 Frame::UndistortKeyPoints

将特征点分配到图像网格中 Frame::AssignFeaturesToGrid

3)Frame::ExtractORB
3-1)作用
主要完成工作是提取图像的ORB特征点和计算描述子
3-2)主要的函数 ComputePyramid ComputeKeyPointsOctTree computeDescriptors

构建图像金字塔 ORBextractor::ComputePyramid

利用四叉树算法均分特征点 ORBextractor::ComputeKeyPointsOctTree

计算某层金字塔图像上特征点的描述子 static ORBextractor::computeDescriptors

3-3)构建图像金字塔 ComputePyramid
3-3-1图像金字塔是什么东东？
首先，图像金字塔的概念是: 图像金字塔是图像中多尺度表达的一种，是一种以多分辨率来解释图像的有效但概念简单的结构。如图：

图片
3-3-2代码怎么实现图像金字塔？
上面讨论了搭建图像金字塔，那怎么搭建呢？ORBSLAM3中，作者调用OpenCV的resize函数实现图像缩放，构建每层金字塔的图像，在函数ORBextractor::ComputePyramid中。

resize(mvImagePyramid[level-1], mvImagePyramid[level], sz, 0, 0, INTER_LINEAR);

3-3-3尺度不变性是什么东东？

我们搭建完金字塔了，但是有个问题，图像的进行了缩放之后，假如要用同一个相机去看，则需要根据缩放的程度来调整相机到图像的距离，来保持其观测的一致性，这就是尺度不变性由来。
在ORB-SLAM3中，为了实现特征尺度不变性采用了图像金字塔，金字塔的缩放因子为1.2。其思路就是对原始图形（第0层）依次进行1/1.2缩放比例进行降采样得到共计8张图片（包括原始图像），然后分别对得到的图像进行特征提取，并记录特征所在金字塔的第几层，这样得到一帧图像的特征点，如图1所示。

现在假设在第二层中有一特征点F，为了避免缩放带来特征点F在纵向的移动，为简化叙述，选择的特征点F位于图像中心，如图2所示。根据相机成像“物近像大，物远像小”的原理，如图2所示为相机成像的示意图。假设图1中摄像机原始图像即金字塔第0层对应图2中成像视野I0 ，则图1中图像金字塔第2层图像可以相应对应于图2中成像视野I2 。

有了以上铺垫现在，再来说说，尺度不变性。简单来说，因为图像金字塔对图像进行了缩放，假如要把该层的图像特征点移到其他层上，就要对应的放大图像，同时相机与图像的距离也要对应着进行缩放，保证其尺度不变性。

3-3-4代码哪里用到了尺度不变性？
3-3-4-1MapPoint::PredictScale
ORBSLAM3中，作者调用MapPoint::PredictScale函数，根据地图点到光心的距离，来预测一个类似特征金字塔的尺度。
因为在进行投影匹配的时候会给定特征点的搜索范围，由于考虑到处于不同尺度(也就是距离相机远近,位于图像金字塔中不同图层)的特征点受到相机旋转的影响不同，因此会希望距离相机近的点的搜索范围更大一点,距离相机更远的点的搜索范围更小一点,所以要在这里,根据点到关键帧/帧的距离来估计它在当前的关键帧/帧中,会大概处于哪个尺度。
可以参考下图示意：

ORB_SLAM3 MapPoint.cc 函数 MapPoint::PredictScale Line 536 539

ratio = mfMaxDistance/currentDist;

int nScale = ceil(log(ratio)/pKF->mfLogScaleFactor);

3-3-4-2MapPoint::UpdateNormalAndDepth
ORBSLAM3中，作者调用MapPoint::UpdateNormalAndDepth函数，来更新平均观测方向以及观测距离范围。由于一个MapPoint会被许多相机观测到，因此在插入关键帧后，需要更新相应变量，创建新的关键帧的时候会调用该函数。上面变量和代码中的对应关系是：

在ORB_SLAM3 MapPoint.cc 函数 MapPoint::UpdateNormalAndDepth Line 490-491

// 观测相机位置到该点的距离上限
mfMaxDistance = dist*levelScaleFactor;
// 观测相机位置到该点的距离下限
mfMinDistance = mfMaxDistance/pRefKF->mvScaleFactors[nLevels-1];

至此，构建图像金字塔 ComputePyramid记录完毕，再来回顾一下，说到底，搭建图像金字塔就是为了在不同尺度上来描述图像，从而达到充分解释图像的目的。
3-4)四叉树算法 ComputeKeyPointsOctTree
其实，代码中，核心算法在ORBextractor::DistributeOctTree中实现的。先讲原理吧。
3-4-1四叉树是什么东东？
装逼地说，啊不，专业地说，四叉树或四元树也被称为Q树（Q-Tree）。四叉树广泛应用于图像处理、空间数据索引、2D中的快速碰撞检测、存储稀疏数据等，而八叉树（Octree）主要应用于3D图形处理。这里可能会有歧义，代码中明明是Octree，不是八叉树吗？为什么这里讲的是四叉树原理呢？其实ORBSLAM里面是用四叉树来均分特征点，后来有人用八叉树来构建和管理地图，可能因为考虑到3D原因，作者在这里才把函数定义成OctTree，但实际用到的是四叉树原理。

QuadTree四叉树顾名思义就是树状的数据结构，其每个节点有四个孩子节点，可将二维平面递归分割子区域。QuadTree常用于空间数据库索引，3D的椎体可见区域裁剪，甚至图片分析处理，我们今天介绍的是QuadTree最常被游戏领域使用到的碰撞检测。采用QuadTree算法将大大减少需要测试碰撞的次数，从而提高游戏刷新性能。
不得不感慨，作者怎么懂那么多？大神就是大神，各种学科专业交叉融合，膜拜。GO ON。
四叉树很简单，就是把一块2d的区域，等分成4份,如下图: 我们把4块区域从右上象限开始编号， 逆时针。

四叉树起始于单节点。对象会被添加到四叉树的单节点上。

3-4-2四叉树用来干嘛？
ORB-SLAM中使用四叉树来快速筛选特征点，筛选的目的是非极大值抑制，取局部特征点邻域中FAST角点相应值最大的点，而如何搜索到这些扎堆的特征点，则采用的是四叉树的分快思想，递归找到成群的点，并从中找到相应值最大的点。
3-4-3代码怎么实现的？
在ORBextractor.cc 函数 ORBextractor::DistributeOctTree
第一部分：

输入图像未分的关键点 对应ORBextractor::DistributeOctTree函数中的形参vToDistributeKeysORBextractor.cc#L537
根据图像区域构造初始的根结点，每个根结点包含图像的一个区域，每个根结点同样包括4个子结点
定义一个提取器 ExtractorNode ni;ORBextractor.cc#L552
设置提取器节点的图像边界 ni.UL ni.UR ni.BL ni.BRORBextractor.cc#L552-L556 
将刚才生成的提取节点添加到列表中lNodes.push_back(ni);ORBextractor.cc#L559 
存储这个初始的提取器节点句柄vpIniNodes[i] = &lNodes.back();ORBextractor.cc#L560
将未分的所有关键点分配给2中构造的根结点，这样每个根节点都包含了其所负责区域内的所有关键点 按特征点的横轴位置，分配给属于那个图像区域的提取器节点vpIniNodes[kp.pt.x/hX]->vKeys.push_back(vToDistributeKeys[i]);ORBextractor.cc#L567
根结点构成一个根结点list，代码中是lNodes用来更新与存储所有的根结点 遍历lNodes，标记不可再分的节点，用的标记变量是lit->bNoMoreORBextractor.cc#L576

第二部分

当列表中还有可分的结点区域的时候：while(!bFinish)ORBextractor.cc#L592
开始遍历列表中所有的提取器节点，并进行分解或者保留：while(lit!=lNodes.end())ORBextractor.cc#L604
判断当前根结点是否可分，可分的意思是，它包含的关键点能够继续分配到其所属的四个子结点所在区域中（左上，右上，左下，右下），代码中是判断标志位if(lit->bNoMore)ORBextractor.cc#L606意思是如果当前的提取器节点具有超过一个的特征点，那么就要进行继续细分
如果可分，将分出来的子结点作为新的根结点放入INodes的前部，e.g. lNodes.front().lit = lNodes.begin();ORBextractor.cc#L626，就是在四个if(n*.vKeys.size()>0)条件中执行。然后将原先的根结点从列表中删除，e.g.lit=lNodes.erase(lit);ORBextractor.cc#L660。由于新加入的结点是从列表头加入的，不会影响这次的循环，该次循环只会处理当前级别的根结点。
当所有结点不可分，e.g(int)lNodes.size()==prevSizeORBextractor.cc#L667，或者结点已经超过需要的点(int)lNodes.size()>=NORBextractor.cc#L667时，跳出循环bFinish = true;ORBextractor.cc#L669。

3-5)计算特征点描述子 computeDescriptors
3-5-1描述子是什么东东？
图像的特征点可以简单的理解为图像中比较显著显著的点，如轮廓点，较暗区域中的亮点，较亮区域中的暗点等。
ORB采用的是哪种描述子呢？是用FAST（features from accelerated segment test）算法来检测特征点。这个定义基于特征点周围的图像灰度值，检测候选特征点周围一圈的像素值，如果候选点周围领域内有足够多的像素点与该候选点的灰度值差别够大，则认为该候选点为一个特征点。

3-5-2计算特征描述子
利用上述步骤得到特征点后，我们需要以某种方式描述这些特征点的属性。
这些属性的输出我们称之为该特征点的描述子（Feature DescritorS）。
ORB采用BRIEF算法来计算一个特征点的描述子。BRIEF算法的核心思想是在关键点P的周围以一定模式选取N个点对，把这N个点对的比较结果组合起来作为描述子。

如上图所示，计算特征描述子的步骤分四步：

3-5-3如何保证描述子旋转不变性?
在现实生活中，我们从不同的距离，不同的方向、角度，不同的光照条件下观察一个物体时，物体的大小，形状，明暗都会有所不同。但我们的大脑依然可以判断它是同一件物体。理想的特征描述子应该具备这些性质。即，在大小、方向、明暗不同的图像中，同一特征点应具有足够相似的描述子，称之为描述子的可复现性。当以某种理想的方式分别计算描述子时，应该得出同样的结果。即描述子应该对光照（亮度）不敏感，具备尺度一致性（大小 ），旋转一致性（角度）等。
前面为了解决尺度一致性问题，采用了图像金字塔来改善这方面的性能。而现在，主要解决BRIEF描述子不具备旋转不变性的问题。
那我们如何来解决该问题呢？
在当前关键点P周围以一定模式选取N个点对，组合这N个点对的T操作的结果就为最终的描述子。当我们选取点对的时候，是以当前关键点为原点，以水平方向为X轴，以垂直方向为Y轴建立坐标系。当图片发生旋转时，坐标系不变，同样的取点模式取出来的点却不一样，计算得到的描述子也不一样，这是不符合我们要求的。因此我们需要重新建立坐标系，使新的坐标系可以跟随图片的旋转而旋转。这样我们以相同的取点模式取出来的点将具有一致性。
打个比方，我有一个印章，上面刻着一些直线。用这个印章在一张图片上盖一个章子，图片上分处直线2头的点将被取出来。印章不变动的情况下，转动下图片，再盖一个章子，但这次取出来的点对就和之前的不一样。为了使2次取出来的点一样，我需要将章子也旋转同一个角度再盖章。（取点模式可以认为是章子上直线的分布情况）
ORB在计算BRIEF描述子时建立的坐标系是以关键点为圆心，以关键点P和取点区域的质心Q的连线为X轴建立2维坐标系。P为关键点。圆内为取点区域，每个小格子代表一个像素。现在我们把这块圆心区域看做一块木板，木板上每个点的质量等于其对应的像素值。根据积分学的知识我们可以求出这个密度不均匀木板的质心Q。

我们知道圆心是固定的而且随着物体的旋转而旋转。当我们以PQ作为坐标轴时，在不同的旋转角度下，我们以同一取点模式取出来的点是一致的。这就解决了旋转一致性的问题。
3-5-4如何计算上面提到的质心？灰度质心法
说到解决该问题，这就不得不提到关键函数static IC_Angle ORBextractor.cc#L75 这个计算的方法是大家耳熟能详的灰度质心法：以几何中心和灰度质心的连线作为该特征点方向。具体是什么原理呢？
其实原理网上很多文章讲解的很多了，我就直接贴上公式了。

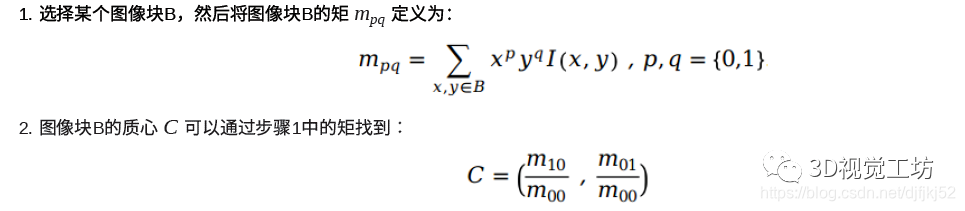
3-5-5代码如何实现？

首先取出关键点P。const uchar* centerORBextractor.cc#L79
因为实现中利用了一个技巧，就是同时计算圆对称上下两条线的和，这样可以加速计算过程。所以计算中间的一条线上的点的和进行单独处理。m_10 += u * center[u];ORBextractor.cc#L82
要在一个图像块区域HALF_PATCH_SIZE中循环计算得到图像块的矩，这里结合四叉树算法，要明白在ORBSLAM中一个图像块区域的大小是30，而这里说过，用了一个技巧是同时计算两条线，因此分一半，就是15，所以HALF_PATCH_SIZE=15
一条直线上的像素坐标开头和结尾分别是-d和d，所以for (int u = -d; u <= d; ++u)ORBextractor.cc#L92
位于直线关键点P上方的像素点坐标是val_plus = center[u + v*step]ORBextractor.cc#L94
位于直线关键点P下方的像素点坐标是val_minus = center[u - v*step]ORBextractor.cc#L94
因为$m_{10}$只和X有关，像素坐标中对应着u，所以$m_{10}$ = X坐标*像素值 = u * (val_plus+val_minus)
因为$m_{01}$只和Y有关，像素坐标中对应着v，所以$m_{01}$ = Y坐标*像素值 = v * v_sum = v * (循环和(val_plus - val_minus))ORBextractor.cc#L95

3-5-6高斯模糊是什么？有什么用？怎么实现？
所谓”模糊”，可以理解成每一个像素都取周边像素的平均值。图中，2是中间点，周边点都是1。“中间点”取”周围点”的平均值，就会变成1。在数值上，这是一种”平滑化”。在图形上，就相当于产生”模糊”效果，”中间点”失去细节。

显然，计算平均值时，取值范围越大，”模糊效果”越强烈。

注意：提取特征点的时候，使用的是清晰的原图像。这里计算描述子的时候，为了避免图像噪声的影响，使用了高斯模糊。
从数学的角度来看，高斯模糊的处理过程就是图像与其正态分布做卷积。

正态分布

我们可以计算当前像素一定范围内的像素的权重，越靠近当前像素权重越大，形成一个符合正态分布的权重矩阵。

卷积

利用卷积算法，我们可以将当前像素的颜色与周围像素的颜色按比例进行融合，得到一个相对均匀的颜色。

卷积核

卷积核一般为矩阵，我们可以将它想象成卷积过程中使用的模板，模板中包含了当前像素周围每个像素颜色的权重。

有了这些基础，我们再来看ORBSLAM到底怎么实现这个高斯模糊的？在代码中，使用的是OpenCV的GaussianBlur函数。
对每层金字塔的图像for (int level = 0; level < nlevels; ++level)ORBextractor.cc#L1105，ORBSLAM都进行高斯模糊：ORBextractor.cc#L1115

GaussianBlur(workingMat, workingMat, Size(7, 7), 2, 2, BORDER_REFLECT_101);

3-5-7怎么实现描述子的计算？
在《3-4-4-2计算特征描述子》说过，BRIEF算法的核心思想是在关键点P的周围以一定模式选取N个点对，把这N个点对的比较结果组合起来作为描述子。
其描述子desc[i]为一个字节val8位，每一位是来自于两个像素点灰度的直接比较：ORBextractor.cc#L124

    t0 = GET_VALUE(0); t1 = GET_VALUE(1);
    val = t0 < t1;       //描述子本字节的bit0
    t0 = GET_VALUE(2); t1 = GET_VALUE(3);
    val |= (t0 < t1) << 1;     //描述子本字节的bit1
    t0 = GET_VALUE(4); t1 = GET_VALUE(5);
    val |= (t0 < t1) << 2;     //描述子本字节的bit2
    t0 = GET_VALUE(6); t1 = GET_VALUE(7);
    val |= (t0 < t1) << 3;     //描述子本字节的bit3
    t0 = GET_VALUE(8); t1 = GET_VALUE(9);
    val |= (t0 < t1) << 4;     //描述子本字节的bit4
    t0 = GET_VALUE(10); t1 = GET_VALUE(11);
    val |= (t0 < t1) << 5;     //描述子本字节的bit5
    t0 = GET_VALUE(12); t1 = GET_VALUE(13);
    val |= (t0 < t1) << 6;     //描述子本字节的bit6
    t0 = GET_VALUE(14); t1 = GET_VALUE(15);
    val |= (t0 < t1) << 7;     //描述子本字节的bit7

每比较出8bit结果，需要16个随机点（参考《3-4-4-1描述子是什么东东？》）。ORBextractor.cc#L121

pattern += 16

其中，定义描述子是32个字节长，所以ORBSLAM的描述子一共是32*8=256位组成。
在《3-4-4-3如何保证描述子旋转不变性?》中说过，ORBSLAM的描述子是带旋转不变性的，有些人评价说这可能也是ORB-SLAM的最大贡献（知识有限，无法做评价，只是引入，无关对错），这么重要的地方具体体现在代码的哪里呢？作者定义了一共局部宏ORBextractor.cc#L116

#define GET_VALUE(idx) center[cvRound(pattern[idx].xb + pattern[idx].ya)step + cvRound(pattern[idx].xa - pattern[idx].y*b)]

其中，a = (float)cos(angle)和b = (float)sin(angle)
背后的原理呢？可能大家这么多知识点看下来都懵逼了，我自己一次性梳理起来也很凌乱的。那就回顾一下《3-5-3如何保证描述子旋转不变性?》，其实就是把灰度质心法找到的质心Q和特征点P就连成的直线PQ和坐标轴对齐，转个角度，就是二维坐标系的旋转公式

3-6)总结
Frame::ExtractORB 主要完成工作是提取图像的ORB特征点和计算描述子，其主要的函数分别是ComputePyramid、ComputeKeyPointsOctTree和computeDescriptors。
ComputePyramid函数主要完成了构建图像金字塔功能。ComputeKeyPointsOctTree函数使用四叉树法对一个图像金字塔图层中的特征点进行平均和分发。computeDescriptors函数用来计算某层金字塔图像上特征点的描述子。
至此，完成了图像特征点的提取，并且将提取的关键点和描述子存放在mvKeys和mDescriptors中。
4)Frame::UndistortKeyPoints
因为ORB-SLAM3中新增了虚拟相机的模型，论文中提及：

Our goal is to abstract the camera model from the whole SLAM pipeline by extracting all properties and functions related to the camera model (projection and unprojection functions, Jacobian, etc) to separate modules. This allows our system to use any camera model by providing the corresponding camera module.In ORB-SLAM3 library, apart from the pinhole model, we provide the Kannala-Brandt fisheye model.

其实跑TUM_VI的时候，就是用的KannalaBrandt8模型，感兴趣的话可以下载数据集跑跑效果，具体方法可参考文章：

EVO Evaluation of SLAM 4 --- ORB-SLAM3 编译和利用数据集运行（https://blog.csdn.net/shanpenghui/article/details/109354918）

其中，矫正就是用的Pinhole模型，就是针孔相机模型，在代码中有体现Frame.cc#L751

我们针对针孔相机模型来讨论一下。因为知识浅薄，所以想从基础讨论起，大神们可直接略过。
4-1为什么要矫正？

图像成像模型

说到相机成像，就不得不说到初中物理，透视投影。
我们可以将透镜的成像简单地抽象成下图所示：

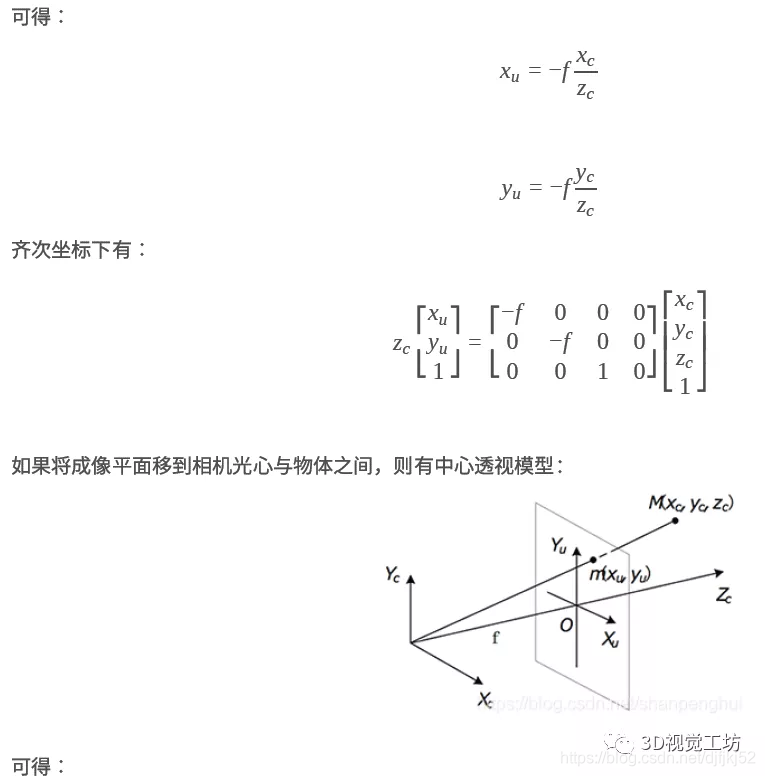
畸变校正

理想的针孔成像模型确定的坐标变换关系均为线性的，而实际上，现实中使用的相机由于镜头中镜片因为光线的通过产生的不规则的折射，镜头畸变（lens distortion）总是存在的，即根据理想针孔成像模型计算出来的像点坐标与实际坐标存在偏差。畸变的引入使得成像模型中的几何变换关系变为非线性，增加了模型的复杂度，但更接近真实情形。畸变导致的成像失真可分为径向失真和切向失真两类：

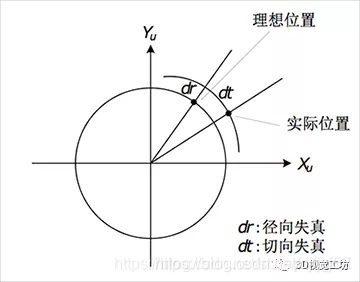
径向畸变（Radial Distortion）

简单来说，由透镜形状（相机镜头径向曲率的不规则变化）引起的畸变称为径向畸变，是导致相机成像变形的主要因素。径向畸变主要分为桶形畸变和枕型畸变。在针孔模型中，一条直线投影到像素平面上还是一条直线。但在实际中，相机的透镜往往使得真实环境中的一条直线在图片中变成了曲线。越靠近图像的边缘现象越明显。由于透镜往往是中心对称的，这使得不规则畸变通常径向对称。（成像中心处的径向畸变最小，距离中心越远，产生的变形越大，畸变也越明显 ）

正向畸变（枕型畸变）：从图像中心开始，径向曲率逐渐增加。
负向畸变（桶形畸变）：边缘的径向曲率小于中心的径向曲率。（鱼眼相机）

实际摄像机的透镜总是在成像仪的边缘产生显著的畸变，这种现象来源于“筒形”或“鱼眼”的影响。如下图，光线在原理透镜中心的地方比靠近中心的地方更加弯曲。对于常用的普通透镜来说，这种现象更加严重。筒形畸变在便宜的网络摄像机中非常厉害，但在高端摄像机中不明显，因为这些透镜系统做了很多消除径向畸变的工作。

切向畸变（Tangential Distortion）

切向畸变是由于相机镜头在制造安装过程中并非完全平行于成像平面造成的。不同于径向畸变在图像中心径向方向上发生偏移变形，切向畸变主要表现为图像点相对理想成像点产生切向偏移。

4-2怎么矫正？
径向畸变模型：r 为像平面坐标系中点(x, y)与图像中心(x0, y0)的像素距离。

切向畸变模型可以描述为：$p_1$和$p_2$，镜头的切向畸变系数。

所以要想矫正图像，最终需要得到的5个畸变参数：

我们来理一理矫正和不矫正坐标之间的关系。

4-3代码怎么实现？
ORBSLAM中，用内参对特征点去畸变。

首先判断是否需要去畸变。

if(mDistCoef.at(0)==0.0)

利用OpenCV的函数进行矫正

cv::undistortPoints(mat,mat, static_cast<Pinhole*>(mpCamera)->toK(),mDistCoef,cv::Mat(),mK);

具体实现就不展开了，感兴趣可以找OpenCV相关资料。
5)Frame::AssignFeaturesToGrid
将图片分割为64*48大小的栅格，并将关键点按照位置分配到相应栅格中，从而降低匹配时的复杂度，实现加速计算。举个例子：

当我们需要在一条图片上搜索特征点的时候，是按照grid搜索还是按照pixel搜索好？毫无疑问，先粗（grid）再细（pixel）搜索效率比较高。
这也是Frame::GetFeaturesInArea函数里面用的方法，变量mGrid联系了 AssignFeaturesToGrid 的结果和其他函数：Frame.cc#L676

for(int ix = nMinCellX; ix<=nMaxCellX; ix++)
{
for(int iy = nMinCellY; iy<=nMaxCellY; iy++)
{
const vector<size_t> vCell = (!bRight) ? mGrid[ix][iy] : mGridRight[ix][iy];

而mGrid这个结果在代码中，后面的流程里，有几个函数都要用：

SearchForInitialization 函数 单目初始化中用于参考帧和当前帧的特征点匹配
SearchByProjection 函数 通过投影地图点到当前帧，对Local MapPoint进行跟踪

具体怎么分配呢？

先分配空间

mGrid[i][j].reserve(nReserve);

如果找到特征点所在网格坐标，将这个特征点的索引添加到对应网格的数组mGrid中

if(PosInGrid(kp,nGridPosX,nGridPosY))
mGrid[nGridPosX][nGridPosY].push_back(i);

6)总结
总而言之，Frame起到的是前端的作用，主要的作用完成对图像特征点进行提取以及描述子的计算：

1. 通过构建图像金字塔，多尺度表达图像，提高抗噪性；
2. 根据尺度不变性，计算相机与各图层图像的距离，准备之后的计算；
3. 利用四叉树的快分思想，快速筛选特征点，避免特征点扎堆；
4. 利用灰度质心法解决BRIEF描述子不具备旋转不变性的问题，增强了描述子的鲁棒性；
5. 利用相机模型，对提取的特征点进行畸变校正；
6. 最终通过大网格形式快速分配特征点，加速了运行速度。

初始化主要函数
ORBSLAM单目视觉SLAM的追踪器接口是函数TrackMonocular，调用了GrabImageMonocular，其下面有2个主要的函数：Frame::Frame()和Tracking::Track()，本文和上篇都是按照以下框架流程来分解单目初始化过程，上篇记录了Frame::Frame()，

本文就记录Tracking::Track()

https://mp.weixin.qq.com/s/jtcji5hONrfUoKX9u3T4Ow

1 Tracking作用
ORB-SLAM3的Tracking部分作用论文已提及，包含输入当前帧、初始化、相机位姿跟踪、局部地图跟踪、关键帧处理、姿态更新与保存等，如图。

2 两个主要函数
单目地图初始化函数是Tracking::MonocularInitialization，其主要是调用以下两个函数完成了初始化过程，ORBmatcher::SearchForInitialization和KannalaBrandt8::ReconstructWithTwoViews，前者用于参考帧和当前帧的特征点匹配，后者利用构建的虚拟相机模型，针对不同相机计算基础矩阵和单应性矩阵，选取最佳的模型来恢复出最开始两帧之间的相对姿态，并进行三角化得到初始地图点。

三 ORBmatcher::SearchForInitialization

这个函数的主要作用是构建旋转角度直方图，选取最优的三个Bin，也就是占据概率最大的三个Bin，如图（数字3被异形吃掉了^-）。因为当前帧会提取到诸多特征点，每一个都可以作为图像旋转角度的测量值，我们希望能在诸多的角度值中，选出最能代表当前帧的旋转角度的测量值，这就是为什么要在旋转角度直方图中选最优的3个Bin的原因

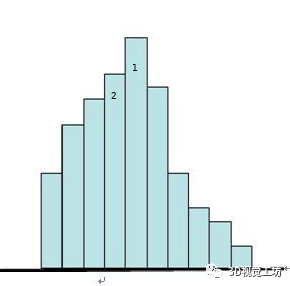
这个旋转的角度哪来的呢？就是在计算描述子的时候算的，调用函数IC_Angle,代码是：ORBextractor.cc#L475

keypoint->angle = IC_Angle(image, keypoint->pt, umax);

感兴趣的同学想知道为什么要这么麻烦的选取最优3个角度，请从旋转不变性开始理解，原理参见：3-5-3如何保证描述子旋转不变性?

（https://blog.csdn.net/shanpenghui/article/details/109809723#t20）

2 位姿估计

主要由函数TwoViewReconstruction::Reconstruct完成，涉及到的知识点又多又关键的，包括对极约束、八点法、归一化、直接线性变换、卡方检验、重投影等，先从主要流程开始理解。

利用随机种子DUtils::Random::SeedRandOnceTwoViewReconstruction.cc#L79，在所有匹配特征点对中随机选择8对匹配特征点为一组for(size_t j=0; j<8; j++)TwoViewReconstruction.cc#L86，用于估计H矩阵和F矩阵。
将当前帧和参考帧中的特征点坐标进行归一化。TwoViewReconstruction::NormalizeTwoViewReconstruction.cc#L753
用DLT方法求解F矩阵 TwoViewReconstruction::ComputeF21TwoViewReconstruction.cc#L273
对给定的F矩阵打分,需要使用到卡方检验的知识 TwoViewReconstruction::CheckFundamentalTwoViewReconstruction.cc#L395
利用得到的最佳模型（选择得分较高的矩阵值，单应矩阵H或者基础矩阵F）估计两帧之间的位姿，代码中对应着函数ReconstructH或ReconstructF。其中，分两个步骤。第一是利用基础矩阵F和本质矩阵E的关系，计算出四组解。第二是调用的函数CheckRT作用是用R，t来对特征匹配点三角化，并根据三角化结果判断R,t的合法性。最终可以得到最优解的条件是位于相机前方的3D点个数最多并且三角化视差角必须大于最小视差角。

估计两帧之间的位姿（包括对极约束、八点法、归一化、直接线性变换、卡方检验、重投影等）

2.2.4 基础矩阵Fundamental 代数推导

有了以上的示意，我们尝试用数学公式描述极点、极线和极平面之间的关系。看了好几篇文章，感觉还是视觉十四讲里面的代数推导比较明晰，我就直接参考过来，当做记录了，其他比较杂乱，记录在《SLAM 学习笔记 本质矩阵E、基础矩阵F、单应矩阵H的推导》（https://blog.csdn.net/shanpenghui/article/details/110133454），感兴趣的同学可以看看。

设以第一个相机作为坐标系三维空间的点：

2.2.6 结尾

由于知识有限，加上篇幅限制，就不再展开了，这里可以参考另外几篇比较好的文章，有比较详细的推导过程，想深入研究的童鞋可以看看。

1、SLAM入门之视觉里程计(3)：两视图对极约束 基础矩阵

2、SLAM基础知识总结（https://blog.csdn.net/MyArrow/article/details/53704339）

五、总结

单目方案的初始化过程再梳理一下：

对极约束是原理基础，从物理世界出发描述了整个视觉相机成像、数据来源以及相互关系的根本问题，其中印象最深的是把搜索匹配点的范围缩小成一段极线，大大加速了匹配过程。
八点法从求解的角度出发，用公式描述了获得我们想要的解的最小条件，提供了有力的数学基础。
归一化使图像进行缩放，而缩放尺度是为了让噪声对于图像的影响在一个数量级上，从而减少噪声对图像的影响。
直接线性转换则从诸多的测量值中（超过8点的N个匹配点，超定方程）算出了最优的解，使我们基本得到了想要的解。
在已经有的粗解基础上利用统计学方法进行分析，筛选出优质的点（符合概率模型的内点）来构成我们最终使用的一个投影的最优解，利用两帧图像上匹配点对进行相互投影，综合判断内外点，从而最小化误差。
筛选出内外点之后，对两个模型进行打分，选出最优模型，然后通过三角化测量进行深度估计，最终完成初始化过程。

至此，单目的初始化过程（基于基础矩阵F）就完啦，内容较多，希望不对的地方多多指教，相互学习，共同成长。以上仅是个人见解，如有纰漏望各位指出，谢谢。

参考：

1.对极几何及单应矩阵https://blog.csdn.net/u012936940/article/details/80723609

2.2D-2D：对极约束https://blog.csdn.net/u014709760/article/details/88059000

3.多视图几何

https://blog.csdn.net/weixin_43847162/article/details/89363281

4.SVD分解及线性最小二乘问题

https://www.cnblogs.com/houkai/p/6656894.html

5.矩阵SVD分解（理论部分II——利用SVD求解最小二乘问题）

https://zhuanlan.zhihu.com/p/64273563

6.奇异值分解(SVD)原理详解及推导

https://blog.csdn.net/zhongkejingwang/article/details/43053513

7.最小二乘解（Least-squares Minimization ）

https://blog.csdn.net/kokerf/article/details/72437294

8.卡方检验 （Chi-square test / Chi-square goodness-of-fit test)

https://blog.csdn.net/zfcjhdq/article/details/83512680?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-3.control&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-3.control

9.样本标准差与自由度 n-1 卡方分布关系的证明

https://blog.csdn.net/robert_chen1988/article/details/90640917

10.证明残差平方和除随机项方差服从卡方分布

https://www.docin.com/p-1185555448.html

11.本质矩阵优化分解的相对位姿估计

http://www.doc88.com/p-6931350248387.html

12.单目移动机器人的相对位姿估计方法

https://www.doc88.com/p-7744747222946.html

13.三角化求深度值（求三位坐标）

https://blog.csdn.net/michaelhan3/article/details/89483148

地图的初始化

https://zhuanlan.zhihu.com/p/337979973

一、前言

单目初始化过程中最重要的是两个函数实现，分别是构建帧（Frame）和初始化（Track）。接下来，就是完成初始化过程的最后一步：地图的初始化，是由CreateInitialMapMonocular函数完成的，本文基于该函数的流程出发，目的是为了结合代码流程，把单目初始化的上下两篇的知识点和ORB-SLAM3整个系统的知识点串联起来，系统化零碎的知识，告诉你平时学到的各个小知识应用在SLAM系统中的什么位置，达到快速高效学习的效果。

二、CreateInitialMapMonocular 函数的总体流程

1. 将初始关键帧，当前关键帧的描述子转为BoW；
2. 将关键帧插入到地图；
3. 用三角测量初始化得到的3D点来生成地图点，更新关键帧间的连接关系；
4. 全局BA优化，同时优化所有位姿和三维点；
5. 取场景的中值深度，用于尺度归一化；
6. 将两帧之间的变换归一化到平均深度1的尺度下；
7. 把3D点的尺度也归一化到1；
8. 将关键帧插入局部地图，更新归一化后的位姿、局部地图点。

三、必备知识

1. 为什么单目需要专门策略生成初始化地图

根据论文《ORB-SLAM: a Versatile and Accurate Monocular SLAM System》，即ORB-SLAM1的论文（中文翻译版ORB-SLAM: a Versatile and Accurate Monocular SLAM System）可知：

1） 单目SLAM系统需要设计专门的策略来生成初始化地图，这也是为什么代码中单独设计一个CreateInitialMapMonocular()函数来实现单目初始化，也是我们这篇文章要讨论的。为什么要单独设计呢？就是因为单目没有深度信息。
2） 怎么解决单目没有深度信息问题？有2种，论文用的是第二种，用一个具有高不确定度的逆深度参数来初始化点的深度信息，该参数会在后期逐渐收敛到真值。
3） 说了ORB-SLAM为什么要同时计算基础矩阵F和单应矩阵H的原因：这两种摄像头位姿重构方法在低视差下都没有很好的约束，所以提出了一个新的基于模型选择的自动初始化方法，对平面场景算法选择单应性矩阵，而对于非平面场景，算法选择基础矩阵。
4）说了ORB-SLAM初始化容易失败的原因：（条件比较苛刻）在平面的情况下，为了保险起见，如果最终存在双重歧义，则算法避免进行初始化，因为可能会因为错误选择而导致算法崩溃。因此，我们会延迟初始化过程，直到所选的模型在明显的视差下产生唯一的解。

2. 共视图 Covisibility Graph

共视图非常的关键，需要先理解共视图，才能更好的理解后续程序中如何设置顶点和边。

2.1 共视图定义

共视图是无向加权图，每个节点是关键帧，如果两个关键帧之间满足一定的共视关系（至少15个共同观测地图点）他们就连成一条边，边的权重就是共视地图点数目。

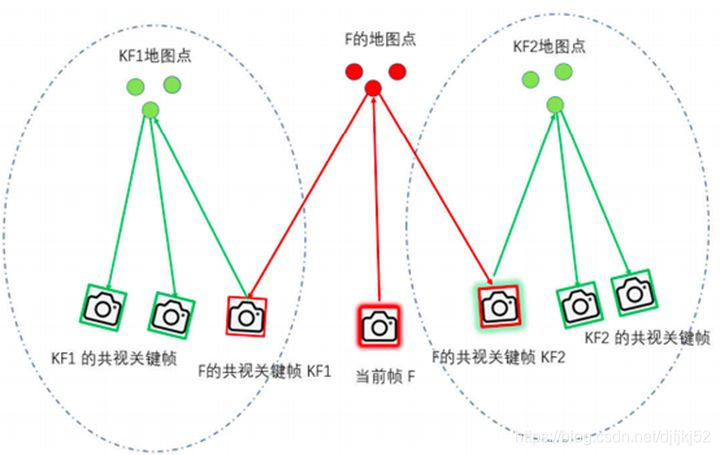
2.2 共视图作用

2.2.1 跟踪局部地图，扩大搜索范围

• Tracking::UpdateLocalKeyFrames()

2.2.2 局部建图里关键帧之间新建地图点

• LocalMapping::CreateNewMapPoints()• LocalMapping::SearchInNeighbors()

2.2.3 闭环检测、重定位检测

• LoopClosing::DetectLoop()、LoopClosing::CorrectLoop()

• KeyFrameDatabase::DetectLoopCandidates

• KeyFrameDatabase::DetectRelocalizationCandidates

2.2.4 优化

• Optimizer::OptimizeEssentialGraph

3. 地图点 MapPoint 和关键帧 KeyFrame

地图点云保存以下信息：

1）它在世界坐标系中的3D坐标

2） 视图方向，即所有视图方向的平均单位向量（该方向是指连接该点云和其对应观测关键帧光心的射线方向）

3）ORB特征描述子，与其他所有能观测到该点云的关键帧中ORB描述子相比，该描述子的汉明距离最小

4）根据ORB特征尺度不变性约束，可观测的点云的最大距离和最小距离

4. 图优化 Graph SLAM

可先看看这些资料《计算机视觉大型攻略 —— SLAM(2) Graph-based SLAM（基于图优化的算法)》，还有《概率机器人学》的第11章，深入理解图优化的概念。

我们在文章开头说过，单目初始化结果得到了三角测量初始化得到的3D地图点Pw，计算得到了初始两帧图像之间的相对位姿（相当于得到了SE(3)），通过相机坐标系Pc和世界坐标系Pw之间的公式，（参考《像素坐标系、图像坐标系、相机坐标系和世界坐标系的关系（简单易懂版）》）

得到相机坐标系的坐标Pc，但是这样还是不能和像素坐标比较。我们接着通过相机坐标系Pc和像素坐标系P(u,v)之间的公式：

5. g2o使用方法

一般来说，g2o的使用流程如下：

5.1创建一个线性求解器LinearSolver
5.2创建BlockSolver，并用上面定义的线性求解器LinearSolver初始化
5.3创建总求解器solver，并从GN, LM, DogLeg 中选一个，再用上述块求解器BlockSolver初始化
5.4创建终极大boss 稀疏优化器（SparseOptimizer），并用已定义的总求解器solver作为求解方法
5.5定义图的顶点和边，并添加到稀疏优化器（SparseOptimizer）中
5.6设置优化参数，开始执行优化

四、代码

1. 将初始关键帧，当前关键帧的描述子转为BoW

pKFini->ComputeBoW();
pKFcur->ComputeBoW();

不展开词袋BoW，只需要知道一点，就是我们在回环检测的时候，需要用到词袋向量mBowVec和特征点向量mFeatVec，所以这里要计算。

2. 向地图添加关键帧

mpAtlas->AddKeyFrame(pKFini);
mpAtlas->AddKeyFrame(pKFcur);

3. 生成地图点，更新图（节点和边）

3.1 遍历

for(size_t i=0; i<mvIniMatches.size();i++)

因为要用三角测量初始化得到的3D点，所以外围是一个大的循环，遍历三角测量初始化得到的3D点mvIniP3D。

3.2 检查

if(mvIniMatches[i]<0)continue;

没有匹配的点，则跳过。

3.3 构造点

cv::Mat worldPos(mvIniP3D[i]);

用三角测量初始化得到的3D点mvIniP3D[i]作为空间点的世界坐标 worldPos。

MapPoint* pMP = new MapPoint(worldPos,pKFcur,mpAtlas->GetCurrentMap());

然后用空间点的世界坐标 worldPos构造地图点 pMP。

3.4 修改点属性

3.4.1 添加可以观测到该地图点pMP的关键帧

pMP->AddObservation(pKFini,i);
pMP->AddObservation(pKFcur,mvIniMatches[i]);

3.4.2 计算该地图点pMP的描述子

pMP->ComputeDistinctiveDescriptors();

因为ORBSLAM是特征点方法，描述子非常重要，但是一个地图点有非常多能观测到该点的关键帧，每个关键帧都有相对该地图点的值（距离和角度）不一样的描述子，在这么多的描述子中，如何选取一个最能代表该点的描述子呢？这里作者用了距离中值法，意思就是说，最能代表该地图点的描述子，应该是与其他描述子具有最小的距离中值。举个栗子，现有描述子A、B、C、D、E、F、G，它们之间的距离分别是1、1、2、3、4、5，求最小距离中值的描述子：

把它们的距离做成2维vector行列的形式，如下：

对每个关键帧得到的描述子与其他描述子的距离进行排序。然后，中位数是median = vDists[0.5*(N-1)]=0.5×(7-1)=3，得到：

可以看到，描述子B具有最小距离中值，所以选择描述子B作为该地图点的描述子。

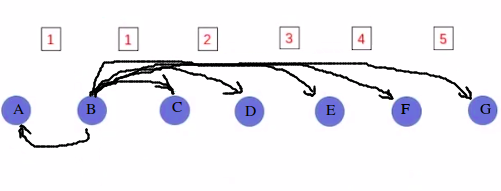
上述例子比较容易理解，但实际问题是，描述子是一个值，如何描述一个值和另一个值的距离呢？我们可以把两个值看成是两个二进制串，而描述两个二进制串之间的距离可以用汉明距离，指的是其不同位数的个数。这样，我们就可以求出两个描述子之间的距离了。

3.4.3 更新该地图点pMP的平均观测方向和深度范围

pMP->UpdateNormalAndDepth();

由于一个地图点会被许多相机观测到，因此在插入关键帧后，需要更新相应变量，创建新的关键帧的时候会调用该地图点。而图像提取描述子是使用金字塔分层提取，所以计算法向量和深度可以知道该地图点在对应的关键帧的金字塔哪一层可以提取到。明确了目的，下一步就是方法问题，所谓的法向量，就是也就是说相机光心指向地图点的方向，计算这个方向方法很简单，只需要用地图点的三维坐标mWorldPos减去相机光心的三维坐标Ow就可以。可是，能观测到该地图点的不止一个关键帧，是个关键帧集合，每个关键帧都有各自的相机光心Owi，我们可以假设一下，有地图点P，有3个关键帧可观测到该点，3个关键帧的相机光心分别是A、B、C，则三个光心到地图点的向量分别是： [公式] 因为通过向量加法可以抵消掉朝向地图点的其他方向上的量，所以最终该地图点的法向量就是三个光心到该地图点的向量的和 :

知道方法之后，我们看程序里面MapPoint::UpdateNormalAndDepth()如何实现：

3.4.3.1 获取地图点信息

observations=mObservations; // 获得观测到该地图点的所有关键帧
pRefKF=mpRefKF;             // 观测到该点的参考关键帧（第一次创建时的关键帧）
Pos = mWorldPos.clone();    // 地图点在世界坐标系中的位置

我们要获得观测到该地图点的所有关键帧，用来找到每个关键帧的光心Owi。还要获得观测到该点的参考关键帧（即第一次创建时的关键帧），因为这里只是更新观测方向，距离还是用参考关键帧到该地图点的距离，体现在后面dist = cv::norm(Pos - pRefKF->GetCameraCenter())。还要获得地图点在世界坐标系中的位置，用来计算法向量。

3.4.3.2 计算该地图点的法向量

cv::Mat normal = cv::Mat::zeros(3,1,CV_32F);
int n=0;
for(map<KeyFrame*,size_t>::iterator mit=observations.begin(), mend=observations.end(); mit!=mend; mit++)
{
KeyFrame* pKF = mit->first;tuple<int,int> 
indexes = mit -> second;
int leftIndex = get<0>(indexes), rightIndex = get<1>(indexes);
if(leftIndex != -1)
{
cv::Mat Owi = pKF->GetCameraCenter();
cv::Mat normali = mWorldPos - Owi;
normal = normal + normali/cv::norm(normali);
n++;
}
if(rightIndex != -1)
{
cv::Mat Owi = pKF->GetRightCameraCenter();
cv::Mat normali = mWorldPos - Owi;normal = normal + normali/cv::norm(normali);n++;
}
}

遍历能观测到该地图点的所有关键帧，获取不同的光心坐标Owi。用地图点的三维坐标mWorldPos减去相机光心的三维坐标Ow计算向量，然后归一化为单位向量，对初始单位向量normal和归一化后的单位向量normali/cv::norm(normali)进行求和，最终除以总数n得到该地图点的朝向mNormalVector = normal/n。ORB-SLAM3在这里添加了双目相机的光心坐标计算。

3.4.3.3 计算该地图点到图像的距离

cv::Mat PC = Pos - pRefKF->GetCameraCenter();
const float dist = cv::norm(PC);

计算参考关键帧相机指向地图点的向量，利用该向量求该地图点的距离。

3.4.3.4 更新该地图点的距离上下限

// 观测到该地图点的当前帧的特征点在金字塔的第几层
    tuple<int ,int> indexes = observations[pRefKF];
    int leftIndex = get<0>(indexes), rightIndex = get<1>(indexes);
    int level;
    if(pRefKF -> NLeft == -1){
        level = pRefKF->mvKeysUn[leftIndex].octave;
    }
    else if(leftIndex != -1){
        level = pRefKF -> mvKeys[leftIndex].octave;
    }
    else{
        level = pRefKF -> mvKeysRight[rightIndex - pRefKF -> NLeft].octave;
    }
    //const int level = pRefKF->mvKeysUn[observations[pRefKF]].octave;        
    const float levelScaleFactor =  pRefKF->mvScaleFactors[level];          // 当前金字塔层对应的缩放倍数
    const int nLevels = pRefKF->mnScaleLevels;                              // 金字塔层数
    {
        unique_lock<mutex> lock3(mMutexPos);
        // 使用方法见PredictScale函数前的注释
        mfMaxDistance = dist*levelScaleFactor;                              // 观测到该点的距离上限
        mfMinDistance = mfMaxDistance/pRefKF->mvScaleFactors[nLevels-1];    // 观测到该点的距离下限
        mNormalVector = normal/n;                                           // 获得地图点平均的观测方向
    }

回顾之前的知识

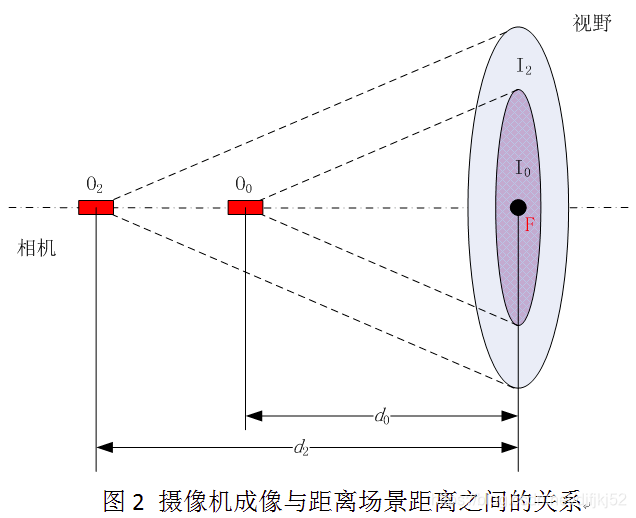
3.5 添加地图点到地图

mpAtlas->AddMapPoint(pMP);

3.6 更新图

非常重要的知识点，好好琢磨，该过程由函数UpdateConnections完成，深入其中看看有什么奥妙。

3.6.1 统计共视帧

// 遍历每一个地图点
for(vector<MapPoint*>::iterator vit=vpMP.begin(), vend=vpMP.end(); vit!=vend; vit++)
…
// 统计与当前关键帧存在共视关系的其他帧
map<KeyFrame*,size_t> observations = pMP->GetObservations();
for(map<KeyFrame*,size_t>::iterator mit=observations.begin(), mend=observations.end(); mit!=mend; mit++)
…
// 体现了作者的编程功底，很强
KFcounter[mit->first]++;

这里代码主要是想完成遍历每一个地图点，统计与当前关键帧存在共视关系的其他帧，统计结果放在KFcounter。看代码有点费劲，举个栗子：已知有一关键帧F1，上面有四个地图点ABCD，其中，能观测到点A的关键帧是有3个，分别是帧F1、F2、F3。能观测到点B的关键帧是有4个，分别是帧F1、F2、F3、F4。能观测到点C的关键帧是有5个，分别是帧F1、F2、F3、F4、F5。能观测到点D的关键帧是有6个，分别是帧F1、F2、F3、F4、F5、F6。对应关系如下：

总而言之，代码想统计的就是与当前关键帧存在共视关系的其他帧，共视关系是通过能看到同个特征点来描述的，所以，当前帧F1与帧F2的共视关系为4，当前帧F1与帧F3的共视关系为4，当前帧F1与帧F4的共视关系为3，当前帧F1与帧F5的共视关系为2，当前帧F1与帧F6的共视关系为1。

3.6.2 更新共视关系大于一定阈值的边，并找到共视程度最高的关键帧

for(map<KeyFrame*,int>::iterator mit=KFcounter.begin(), mend=KFcounter.end(); mit!=mend; mit++)
{
…
// 找到共视程度最高的关键帧
if(mit->second>nmax)
{
nmax=mit->second;
pKFmax=mit->first;
}
if(mit->second>=th)
{
// 更新共视关系大于一定阈值的边
vPairs.push_back(make_pair(mit->second,mit->first));
// 更新其它关键帧与当前帧的连接权重
(mit->first)->AddConnection(this,mit->second);
}
}

假设共视关系阈值为1，在上面这个例子中，只要和当前帧有共视关系的帧都需要更新边，由于在这之前，关键帧只和地图点之间有连接关系，和其他帧没有连接关系，要构建共视图（以帧为节点，以共视关系为边）就要一个个更新节点之间的边的值。(mit->first)->AddConnection(this,mit->second)的含义是更新其他帧Fi和当前帧F1的边（因为当前帧F1也被当做其他帧Fi的有共视关系的一个）。在遍历查找共视关系最大帧的时候同步做这个事情，可以加速计算和高效利用代码。mit->first在这里，代表和当前帧有共视关系的F2…F6（因为遍历的是KFcounter，存储着与当前帧F1有共视关系的帧F2…F6）。举个栗子，当处理当前帧F1和共视帧F2时，更新与帧F2有共视关系的帧F1，以此类推，当处理当前帧F1和共视帧F3时，更新与帧F3有共视关系的帧F1…。

3.6.3 如果没有连接到关键帧（没有超过阈值的权重），则连接权重最大的关键帧

if(vPairs.empty())
{
vPairs.push_back(make_pair(nmax,pKFmax));
pKFmax->AddConnection(this,nmax);
}

如果每个关键帧与它共视的关键帧的个数都少于给定的阈值，那就只更新与其它关键帧共视程度最高的关键帧的 mConnectedKeyFrameWeights，以免之前这个阈值可能过高造成当前帧没有共视帧，容易造成跟踪失败？（自己猜的）

3.6.4 对共视程度比较高的关键帧对更新连接关系及权重（从大到小）

sort(vPairs.begin(),vPairs.end());
// 将排序后的结果分别组织成为两种数据类型
list<KeyFrame*> lKFs;
list lWs;
for(size_t i=0; i<vPairs.size();i++)
{
// push_front 后变成了从大到小顺序
lKFs.push_front(vPairs[i].second);
lWs.push_front(vPairs[i].first);
}

3.6.5 更新当前帧的信息

…
mConnectedKeyFrameWeights = KFcounter;
mvpOrderedConnectedKeyFrames = vector<KeyFrame*>(lKFs.begin(),lKFs.end());
mvOrderedWeights = vector(lWs.begin(), lWs.end());

3.6.6 更新生成树的连接

…
if(mbFirstConnection && mnId!=mpMap->GetInitKFid())
{
// 初始化该关键帧的父关键帧为共视程度最高的那个关键帧
mpParent = mvpOrderedConnectedKeyFrames.front();
// 建立双向连接关系，将当前关键帧作为其子关键帧
mpParent->AddChild(this);
mbFirstConnection = false;
}

4. 全局BA

全局BA主要是由函数GlobalBundleAdjustemnt完成的，其调用了函数BundleAdjustment，建议开始阅读之前复习一下文章前面的《二、4. 图优化 Graph SLAM》和《二、5. g2o使用方法》，下文直接从函数BundleAdjustment展开叙述。

// 调用
Optimizer::GlobalBundleAdjustemnt(mpAtlas->GetCurrentMap(),20);
// 定义
void Optimizer::GlobalBundleAdjustemnt(Map* pMap, int nIterations, bool* pbStopFlag, const unsigned long nLoopKF, const bool bRobust)
//调用
vector<KeyFrame*> vpKFs = pMap->GetAllKeyFrames();
vector<MapPoint*> vpMP = pMap->GetAllMapPoints();
BundleAdjustment(vpKFs,vpMP,nIterations,pbStopFlag, nLoopKF, bRobust);
// 定义
void Optimizer::BundleAdjustment(const vector<KeyFrame *> &vpKFs, const vector<MapPoint > &vpMP, int nIterations, bool pbStopFlag, const unsigned long nLoopKF, const bool bRobust)

4.1 方程求解器 LinearSolver

4.2 矩阵求解器 BlockSolver

4.3 算法求解器 AlgorithmSolver

用BlockSolver创建方法求解器solver，选择非线性最小二乘解法（高斯牛顿GN、LM、狗腿DogLeg等），AlgorithmSolver是我自己想出来的名字，方便记忆。

4.4 稀疏优化器 SparseOptimizer

g2o::SparseOptimizer optimizer;
optimizer.setAlgorithm(solver);// 用前面定义好的求解器作为求解方法
optimizer.setVerbose(false);// 设置优化过程输出信息用的

用solver创建稀疏优化器SparseOptimizer。

4.5 定义图的顶点和边，添加到稀疏优化器SparseOptimizer

在开始看具体步骤前，注意两点，一是ORB-SLAM3中图的定义，二是其误差模型，理解之后才可能明白为什么初始化过程中要操作这些变量。

4.5.1 图的定义

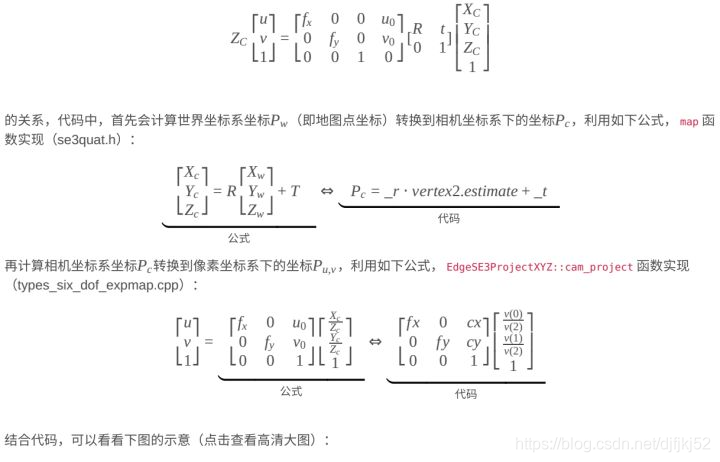
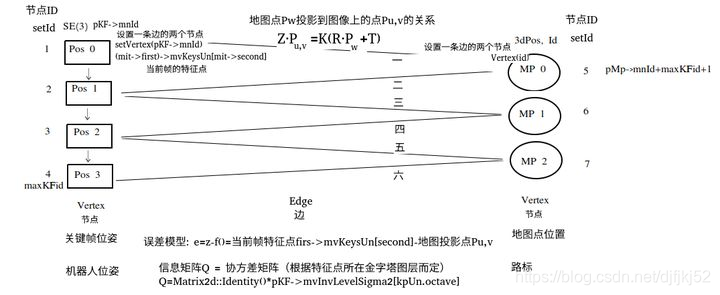
4.5.1.2 设置节点和边的步骤

和把大象放冰箱的步骤一样的简单，设置顶点和边的步骤总共分三步：1. 设置类型是关键帧位姿的节点信息：位姿（SE3）、编号（setId(pKF->mnId)）、最大编号（maxKFid）；2. 设置类型是地图点坐标的节点信息：位姿（3dPos）、编号（setId(pMp->mnId+maxKFid+1)）、计算的变量（setMarginalized）；【为什么要设置setMarginalized，感兴趣的同学可以自己参考一下这篇文章《g2o：非线性优化与图论的结合》，这里就不过多赘述了】3. 设置边的信息：连接的节点（setVertex）、信息矩阵（setInformation）、计算观测值的相关参数（setMeasurement/fx/fy/cx/cy）、核函数（setRobustKernel）。【引入鲁棒核函数是人为降低过大的误差项，可以更加稳健地优化，具体请参考《视觉十四讲》第10讲】

4.5.1.3 ORB-SLAM3新增部分

ORB-SLAM3中新增了单独记录边、地图点和关键帧的容器，比如单目中的vpEdgesMono、vpEdgeKFMono和vpMapPointEdgeMono，分别记录的是误差值、关键帧和地图点，目的是在获取优化后的关键帧位姿时，使用该误差值vpEdgesMono[i]，对地图点vpMapPointEdgeMono[i]进行自由度为2的卡方检验e->chi2()>5.991，以此排除外点，选出质量好的地图点，见源码Optimizer.cc#L337。为了不打断图优化思路，不过多展开ORB-SLAM2和3的区别，感兴趣的同学可自行研究源码。

4.5.2 误差模型

SLAM中要计算的误差如下示意：

4.5.3 步骤一，添加关键帧位姿顶点

// 对于当前地图中的所有关键帧
for(size_t i=0; i<vpKFs.size(); i++)
{
KeyFrame* pKF = vpKFs[i];
// 去除无效的
if(pKF->isBad())
continue;
// 对于每一个能用的关键帧构造SE3顶点,其实就是当前关键帧的位姿
g2o::VertexSE3Expmap * vSE3 = new g2o::VertexSE3Expmap();
vSE3->setEstimate(Converter::toSE3Quat(pKF->GetPose()));
vSE3->setId(pKF->mnId);
// 只有第0帧关键帧不优化（参考基准）
vSE3->setFixed(pKF->mnId==0);
// 向优化器中添加顶点，并且更新maxKFid
optimizer.addVertex(vSE3);
if(pKF->mnId>maxKFid)
maxKFid=pKF->mnId;
}

注意三点：

• 第0帧关键帧作为参考基准，不优化

• 只需设置SE(3)和Id即可

• 需要更新maxKFid，以便下方添加观测值（相机3D位姿）时使用

4.5.4 步骤二，添加地图点位姿顶点

// 卡方分布 95% 以上可信度的时候的阈值
const float thHuber2D = sqrt(5.99);     // 自由度为2
const float thHuber3D = sqrt(7.815);    // 自由度为3
// Set MapPoint vertices
// Step 2.2：向优化器添加MapPoints顶点
// 遍历地图中的所有地图点
for(size_t i=0; i<vpMP.size(); i++)
{
    MapPoint* pMP = vpMP[i];
    // 跳过无效地图点
    if(pMP->isBad())
        continue;
    // 创建顶
    g2o::VertexSBAPointXYZ* vPoint = new g2o::VertexSBAPointXYZ();
    // 注意由于地图点的位置是使用cv::Mat数据类型表示的,这里需要转换成为Eigen::Vector3d类型
    vPoint->setEstimate(Converter::toVector3d(pMP->GetWorldPos()));
    // 前面记录maxKFid 是在这里使用的
    const int id = pMP->mnId+maxKFid+1;
    vPoint->setId(id);
    // g2o在做BA的优化时必须将其所有地图点全部schur掉，否则会出错。
    // 原因是使用了g2o::LinearSolver<BalBlockSolver::PoseMatrixType>这个类型来指定linearsolver,
    // 其中模板参数当中的位姿矩阵类型在程序中为相机姿态参数的维度，于是BA当中schur消元后解得线性方程组必须是只含有相机姿态变量。
    // Ceres库则没有这样的限制
    vPoint->setMarginalized(true);
    optimizer.addVertex(vPoint);

4.5.5 步骤三，添加边

    // 边的关系，其实就是点和关键帧之间观测的关系
    const map<KeyFrame*,size_t> observations = pMP->GetObservations();
    // 边计数
    int nEdges = 0;
    //SET EDGES
    // Step 3：向优化器添加投影边（是在遍历地图点、添加地图点的顶点的时候顺便添加的）
    // 遍历观察到当前地图点的所有关键帧
    for(map<KeyFrame*,size_t>::const_iterator mit=observations.begin(); mit!=observations.end(); mit++)
    {
        KeyFrame* pKF = mit->first;
        // 滤出不合法的关键帧
        if(pKF->isBad() || pKF->mnId>maxKFid)
            continue;
        nEdges++;
        const cv::KeyPoint &kpUn = pKF->mvKeysUn[mit->second];
        if(pKF->mvuRight[mit->second]<0)
        {
            // 如果是单目相机按照下面操作
            // 构造观测
            Eigen::Matrix<double,2,1> obs;
            obs << kpUn.pt.x, kpUn.pt.y;
            // 创建边
            g2o::EdgeSE3ProjectXYZ* e = new g2o::EdgeSE3ProjectXYZ();
            // 填充数据，构造约束关系
            e->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(id)));
            e->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(pKF->mnId)));
            e->setMeasurement(obs);
            // 信息矩阵，也是协方差，表明了这个约束的观测在各个维度（x,y）上的可信程度，在我们这里对于具体的一个点，两个坐标的可信程度都是相同的，
            // 其可信程度受到特征点在图像金字塔中的图层有关，图层越高，可信度越差
            // 为了避免出现信息矩阵中元素为负数的情况，这里使用的是sigma^(-2)
            const float &invSigma2 = pKF->mvInvLevelSigma2[kpUn.octave];
            e->setInformation(Eigen::Matrix2d::Identity()*invSigma2);
            // 如果要使用鲁棒核函数
            if(bRobust)
            {
                g2o::RobustKernelHuber* rk = new g2o::RobustKernelHuber;
                e->setRobustKernel(rk);
                // 这里的重投影误差，自由度为2，所以这里设置为卡方分布中自由度为2的阈值，如果重投影的误差大约大于1个像素的时候，就认为不太靠谱的点了，
                // 核函数是为了避免其误差的平方项出现数值上过大的增长
                rk->setDelta(thHuber2D);
            }
            // 设置相机内参
            // ORB-SLAM2的做法
            //e->fx = pKF->fx;
            //e->fy = pKF->fy;
            //e->cx = pKF->cx;
            //e->cy = pKF->cy;
            // ORB-SLAM3的改变
e->pCamera = pKF->mpCamera;
            optimizer.addEdge(e);
        }
        else
        {
            // 双目或RGBD相机按照下面操作
            ......这里忽略，只讲单目
        }  
    } // 向优化器添加投影边,也就是遍历所有观测到当前地图点的关键帧
    // 如果因为一些特殊原因,实际上并没有任何关键帧观测到当前的这个地图点,那么就删除掉这个顶点,并且这个地图点也就不参与优化
    if(nEdges==0)
    {
        optimizer.removeVertex(vPoint);
        vbNotIncludedMP[i]=true;
    }
    else
    {
        vbNotIncludedMP[i]=false;
    }
}    

4.5.6 优化

optimizer.initializeOptimization();
optimizer.optimize(nIterations);

添加边设置优化参数，开始执行优化。

5. 计算深度中值

   float medianDepth = pKFini->ComputeSceneMedianDepth(2);
   float invMedianDepth = 1.0f/medianDepth

这里开始，5到7是比较关键的转换，要理解这部分背后的含义，我们需要回顾一下相机模型，复习一下各个坐标系之间的转换关系，再看代码就简单多了。

5.1 相机模型与坐标系转换

很多人看了n遍相机模型，小孔成像原理烂熟于心，但那只是烂熟，并没有真正应用到实际，想真正掌握，认真看下去。先复习一下相机投影的过程，也可参考该文[《像素坐标系、图像坐标系、相机坐标系和世界坐标系的关系（简单易懂版）》]，如图（点击查看高清大图）

再来弄清楚各个坐标系之间的转换关系，认真研究下图，懂了之后能解决很多心里的疑问（点击查看高清大图）：

总之，图像上的像素坐标和世界坐标的关系是：

其中，zc是相机坐标系下的坐标；dx和dy分别表示每个像素在横轴x和纵轴y的物理尺寸，单位为毫米/像素；u0,v0表示的是图像的中心像素坐标和图像圆点像素坐标之间相差的横向和纵向像素数；f是相机的焦距，R,T是旋转矩阵和平移矩阵，xw,yw,zw是世界坐标系下的坐标。

5.2 归一化平面

讲归一化平面的资料比较少，可参考性不高。大家也不要把这个东西看的有多玄乎，其实就是一个数学技巧，主要是为了方便计算。从上面的公式可以看到，左边还有个zc的因数，除掉这个因数的过程其实就可以叫归一化。代码中接下来要讲的几步其实都可以归结为以下这个公式：

6. 归一化两帧变换到平均深度为1

cv::Mat Tc2w = pKFcur->GetPose();
// x/z y/z 将z归一化到1
Tc2w.col(3).rowRange(0,3) = Tc2w.col(3).rowRange(0,3)*invMedianDepth;
pKFcur->SetPose(Tc2w);

7. 3D点的尺度归一化

vector vpAllMapPoints = pKFini->GetMapPointMatches();
for (size_t iMP = 0; iMP < vpAllMapPoints.size(); iMP++)
{
if (vpAllMapPoints[iMP])
{
MapPointPtr pMP = vpAllMapPoints[iMP];
if(!pMP->isBad())
pMP->SetWorldPos(pMP->GetWorldPos() * invMedianDepth);
}
}

8. 将关键帧插入局部地图

   mpLocalMapper->InsertKeyFrame(pKFini);
   mpLocalMapper->InsertKeyFrame(pKFcur);
   mCurrentFrame.SetPose(pKFcur->GetPose());
   mnLastKeyFrameId = pKFcur->mnId;
   mnLastKeyFrameFrameId=mCurrentFrame.mnId;
   mpLastKeyFrame = pKFcur;
   mvpLocalKeyFrames.push_back(pKFcur);
   mvpLocalKeyFrames.push_back(pKFini);
   mvpLocalMapPoints = mpMap->GetAllMapPoints();
   mpReferenceKF = pKFcur;
   mCurrentFrame.mpReferenceKF = pKFcur;
   mLastFrame = Frame(mCurrentFrame);
   mpMap->SetReferenceMapPoints(mvpLocalMapPoints);
   {
   unique_lock lock(mMutexState);
   mState = eTrackingState::OK;
   }
   mpMap->calculateAvgZ();
   // 初始化成功，至此，初始化过程完成

五、总结

总之，初始化地图部分，重要的支撑在于两个点：1. 理解图优化的概念，包括ORB-SLAM3是如何定义图的，顶点和边到底是什么，他们有什么关系，产生这种关系背后的公式是什么，搞清楚这些，图优化就算入门了吧，也可以看得懂地图初始化部分了；
2. 相机模型，以及各个坐标系之间的关系，大多数人还是停留在大概理解的层面，需要结合代码实际来加深对它的理解，因为整个视觉SLAM就是多视图几何理论的天下，不懂这些就扎近茫茫代码中，很容易迷失。
至此，初始化过程完结了。我们通过初始化过程认识了ORB-SLAM3系统，但只是管中窥豹，看不到全面，想要更加深入的挖掘，还是要多多拆分源码，一个个模块掌握，然后才能转化成自己的东西。以上都是各人见解，如有纰漏，请各位不吝赐教，O(∩_∩)O谢谢。
六、参考

1. ORB-SLAM: a Versatile and Accurate Monocular SLAM System

2. ORB-SLAM3 细读单目初始化过程（上）

3. 理解图优化，一步步带你看懂g2o代码

4. ORB-SLAM2 代码解读（三）：优化 1（概述）

5. [视觉slam十四讲

6.非线性优化](https://blog.csdn.net/weixin_42905141/article/details/92993097#2_59)6. 《视觉十四讲》 高翔

7. Mur-Artal R , Tardos J D . ORB-SLAM2: an Open-Source SLAM System for Monocular, Stereo and RGB-D Cameras[J]. IEEE Transactions on Robotics, 2017, 33(5):1255-1262.8. Campos C , Elvira R , Juan J. Gómez Rodríguez, et al. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual-Inertial and Multi-Map SLAM[J]. 2020.9. 《概率机器人》 [美] Sebastian Thrun / [德] Wolfram Burgard / [美] Dieter Fox 机械工业出版社