模式识别（Pattern Recognition）学习笔记（二十）--BP算法

1.引言

       在无法像线性感知器一样利用梯度下降学习参数这一问题阻碍了MLP长达25年后的一天，有人给出了一种有效的求解这些参数的方法，就是大名鼎鼎的反向传播算法（Back Propagation），简称为我们熟知的BP算法（特别注意，BP算法是一种算法，一种机器学习算法，而并非一种网络或模型）。BP的主要突破，在于用Sigmoid函数替代了原始MLP中的阶跃函数作为网络的传递函数。

2.传递函数的比较

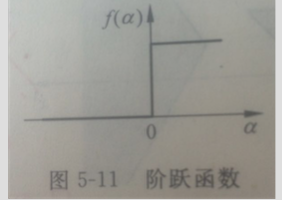
2.1阶跃函数

        阶跃函数的函数曲线如图所示：

不难看出，阶跃函数的性质，它在零点处不可导；

2.2Sigmoid函数

         Sigmoid函数的函数曲线如图所示：

       从曲线图中可以看出，在第一象限，S函数其实与阶跃函数一样，不同的在第二象限，后者是从1骤变到0，而前者的变化就相对比较平缓和平滑，并且它的曲线形状比较像一个‘S’，所以又叫S型函数。

S函数的函数表达式为：

            （1）

取值范围为0和1之间，可以被看作是对阶跃函数的一种渐进曲线，而对于符号函数来说，可以用下面的形式来逼近：

取值范围（-1,1）;

S函数作为神经元的传递函数，得到：

                    (2)

       可能心细的朋友会发现，这里不是应该还有个常数常数权值项的嘛，对没错，但是为了书写和讨论简便，将常数权值作为一个固定输入1的权值合并到加权求和中，并且下标仍然从1到n；

      另外，从上图中可以看到，S函数是单调递增的非线性函数，无限次可微，并且当权值较大时可以逼近出阶跃函数，当权值较小时逼近线性函数。

3.再谈人工神经网络（ANN）

       人工神经网络的研究从上世纪80年代中期开始得到了迅猛的发展，而其中多层感知器BP学习算法的突破是其中一个重要的原因，于是那时起，”人工神经网络“一词开始成为机器学习领域使用对多的词汇之一，而多层感知器则是其中的典型代表，注意，现在的人工神经网络并非专指多层感知器，毕竟还有很多其他类型的神经网络。

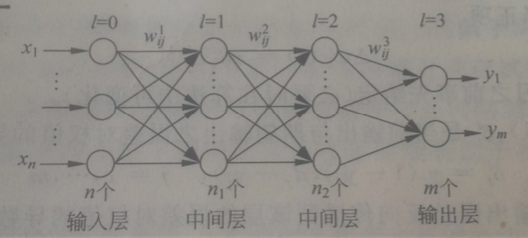
       典型的人工神经网络模型包括如下层：输入层、隐含层、输出层；类似这种形式的神经网络（以下简称为NN）被称为前馈型的NN，是NN的主要结构形式之一。前馈型NN中，信号沿着从输入层到输出层的方向单向流动，输入层把信号传递给隐层，（如果有多个隐层）隐层再把信号传递给下一隐层，这种NN实现的是从输入层到输出层的函数映射，把一个样本特征向量的每一维分量分别输入到网络输入层的各个对应节点上，经过在网络上从前向后的一系列运算，最后在输出端得到相应的输出值或向量。

       通常来说，NN的层数是这么定义的：我们一般所说的一个多少层的NN，指的是包含输入层、多个隐层和输出层全部在内的网络；但也有人觉得输入层和输出层是一个NN的基本层结构，所以没必要计算在内，所以对于一个四层的NN来说，他会说是一个2层的；为了避免歧义，最好说成：一个带有xx个隐层的NN模型。

       不同的NN结构，不同的传递函数，以及采用不同的权值设定方法，都决定了最后构成NN的不同类型。通常，在实际应用中，传递函数往往都是确定的，如前馈型的都是Sigmoid函数；而且NN的结构也是事先设置好的，除了个神经元连接的权重，它们是需要通过训练样本学习而来的。关于训练样本，其实是一堆带有输出标签的样本，即x和y都已知，网络采用的学习算法会根据这些样本来对各权值进行调整，使得该网络最终能够很好地逼近x到y的函数映射关系。

3.BP算法的基本原理及推导

        为了阐述便捷，首先给出NN的一个参照图：

对应上图给出以下变量约定：

设输入向量为n维，;输入向量为m维（即输出层有m个节点），;

设总层数为L层，输出层为L-1层；其中上标l表示所在的层；

：第l层第i个神经元的输出；

：第l层的权值，其中上标l表示所在层，下表ij表示所连接的两个节点，因此就是第l-1层的节点i连接到第l层的节点j的权值；

：在第t次迭代或t时刻的的取值；

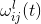
目标函数：网络在所有训练样本上的预测输出与期望输出之间的均方误差；

目标函数的求解方法：梯度下降法；

基本思路：

训练开始之前，随机选择各权值的初始值；

训练过程中，轮流将每个训练样本送入网络；

当一个样本被送到网络输入端后，利用初始的权值计算得到该样本的预测输出；

在期望输出已知的情况下，计算出网络输出与期望输出之间的均方误差；

计算出该误差对输出层各权值的偏导数，然后往负梯度方向对上述权值进行修正；

同上，对倒数第二层，也就是隐层的最后一层，同样进行修正；

以此类推，直到把各层的权值都修正一次；

对下一个训练样本开始进行同样的训练过程，如此不断进行下去，直到在一轮训练中总的误差水平达到预设阈值；

       上述学习过程中，正是归功于这种误差的反向传播到各隐层节点，才得以实现对中间各层的权值进行学习，所以误差反传是关键，正因为如此，人们把这种神经网络的权值学习算法称作所谓的BP算法；另外由于该学习算法是MLP中的标准学习算法，也有很多人干脆直接把带有这种学习算法的前馈型MLP叫做BP网络，所以在这里千万要注意不要混淆有关BP的两种含义。

BP的具体实现步骤和相关推导：

1）确定NN的结构（有关结构的确定，后续会学习，现在假设结构确定），用小随机数对权值初始化，训练时间t=0；

2）从训练集中任意取出一个训练样本x（n维），记其期望的输出为d（m维）（通常，m小于n）;

3）计算样本x输入下当前网络的预测输出：

                                                             r=1,2,...,m                (3)

其中，f(.)是Sigmoid函数；

4）定义网络的总误差：

                               （4）

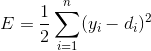
目的是通过调整权值w来最小化E；

5）修正各层权值，首先从输出层开始，具体做法如下：

          a .对于第l层，用下面的公式进行修正：

                     （5）

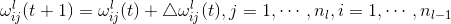
其中，等式右边第二项为权值修正项：

                    （6）

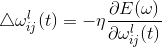
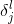
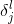
          b.在梯度计算过程中我们引入一个残差项，它由实际输出与期望输出之间的误差计算得来，它的值反映了该节点对最终输出值得残差产生多大的影响；对于最后一层的残差很好计算（记为），计算过程如下：

最后一层有：

                               （7）

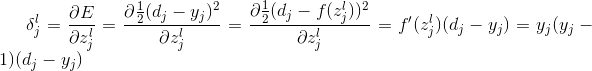
其中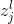为节点的前向输出值，j=1，2，...，m；

另外对Sigmoid函数而言，其有一个性质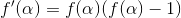：，需要的可自行推导；

           c.对于中间层，即隐层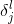，是误差反向传播到该层的误差对权值的导数，即各节点残差的加权求和：

                                  （8）

其中，j = 1,2,...,nl;

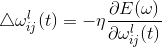
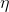
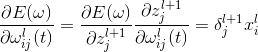
           d.现在我们开始计算，其中是修正步长，必要时可以根据需要变化；

                         （9）

于是，代入公式（5）有：

                                        (10)

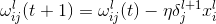
           e.更新完所有权值后对所有训练样本重新计算输出，计算更新后的网络输出与期望输出之间的误差，检查算法终止条件，如果到达终止条件就终止迭代，否则进行下一次迭代，置t=t+1，并跳到步骤2）。

       算法的终止条件通常有三种设置方法：一是在最近一次迭代训练中网络的输出与期望值之间的总误差小于某一预设的阈值；二是在最近一次迭代训练中所有权值的变化小于一定阈值；三是算法达到了预设的总迭代次数。

4.BP小结

       上述介绍的算法，尽管采用了Sigmoid函数，但是仍然可能陷入局部极小，不能保证收敛到全局最优，原因在于，通常情况下，目标函数是权值的复杂的非线性函数，往往有多个极小值点，运用GD算法时，如果收敛到某一个局部极小值点处，梯度就会等于或近似等于0，无法进一步优化目标函数，从而导致了整个学习过程无法收敛到全局最优解，因此研究BP算法的误差收敛过程对于掌握神经网络的学习情况是非常重要的。

       影响BP算法的最终收敛结果的参数有以下几个：

1）有时会受初始权值的影响：各权值初始值不能为0，也不应该相同，应该利用小随机数来选取，所以实际应用中，如果算法很难收敛，就要考虑更换初始权值。

2）修正步长：步长太大，刚开始看起来收敛速度会比较快，但是很容易出现算法震荡而无法收敛或收敛很慢；反之，步长太小，权值调整非常的慢，收敛速度也会非常慢，且一旦陷入局部最优，就容易停在那里不动。通常情况下，步长可选择在0.1~3之间，当然对于不同的网络，也要具体情况具体对待。

       本篇博客介绍的是最基本的BP算法，后续研究中，有很多研究者为了兼顾训练过程和精度，采用变步长的方法训练，就是随着学习的进行，逐步减小步长；另外为了使BP能够更好地收敛，有人提出在权值更新过程中引入“记忆项”，使得本次权值修正的方向不是完全取决于当前样本下的误差梯度方向，还取决于上一次的修正方向，从而避免过早陷入局部最优。