pl_vio线特征·part II

0.引言

• pl_vio线特征·part I

现在CSDN有字数限制了，被迫拆分为两篇文章。

4.线段残差对位姿的导数

• 这一小节理论部分来自这里,当然也是来自原论文。

4.1.直线的观测模型和误差

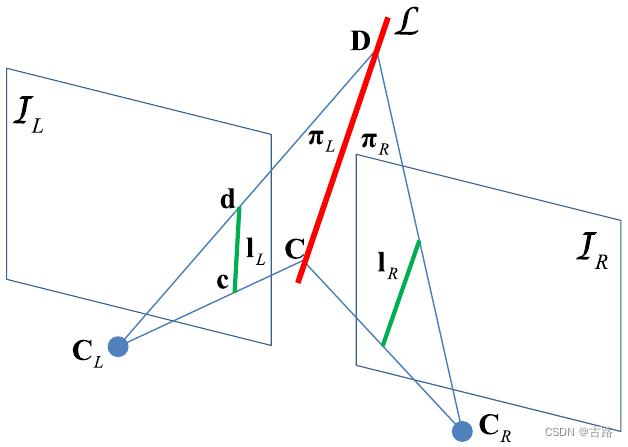
图2 空间直线投影到像素平面
要想知道线特征的观测模型，我们需要知道线特征从归一化平面到像素平面的投影内参矩阵 $\mathcal{K}$ 。如图2，点 $C$ 和 $D$ 是直线 $\mathcal{L}=({\mathbf{n}}^{\top },{\mathbf{d}}^{\top }{)}^{\top }$ 上两点，点 $c$ 和 $d$ 是它们在像素平面上的投影。 $c=KC$,$d=KD$ ,$K$是相机的内参矩阵。 $\mathbf{n}=[C{]}_{\times }D，l=\left[\begin{array}{ccc}{l}_1& l_2& l_3\end{array}\right]=[c{]}_{\times }d$ 。那么有

$$l=\mathcal{K}\mathbf{n}=\left[\begin{array}{ccc}{f}_y& 0& 0\\ 0& f_x& 0\\ -f_y{c}_x& -f_x{c}_y& f_x{f}_y\end{array}\right]\mathbf{n}$$

c叉乘d是法向量，但同时也代表了归一化平面上和这个法向量过原点决定的平面的交线。直线的一般式ax+by+c=0。那么归一化平面上的c和d之间所有的点（x,y）点乘它们的法向量n，也是等于0的。xn1+yn2+n3=0。那么n1，n2，n3就是a，b，c。

$$\begin{array}{rl}{l}^i=c{}^i\times d{}^i& =(KC{}^n)\times (KD{}^n)\\ & ={\left[\begin{array}{c}fx{X}_C+cx\\ fy{Y}_C+cy\\ 1\end{array}\right]}_{\times }\left[\begin{array}{c}fx{X}_D+cx\\ fy{Y}_D+cy\\ 1\end{array}\right]\\ & =\left[\begin{array}{ccc}0& -1& (fy{Y}_C+cy)\\ 1& 0& -(fx{X}_C+cx)\\ -(fy{Y}_C+cy)& (fx{X}_C+cx)& 0\end{array}\right]\left[\begin{array}{c}fx{X}_D+cx\\ fy{Y}_D+cy\\ 1\end{array}\right]\\ & =\left[\begin{array}{c}fy(Y_C-Y_D)\\ fx(X_C-X_D)\\ fxfy(X_C{Y}_D-Y_C{X}_D)+fxcy(X_D-X_C)+fycx(Y_D-Y_C)\end{array}\right]\\ & =\left[\begin{array}{ccc}fy& 0& 0\\ 0& fx& 0\\ -fycx& -fxcy& fxfy\end{array}\right]\left[\begin{array}{c}{Y}_D-Y_C\\ X_D-X_C\\ X_C{Y}_D-Y_C{X}_D\end{array}\right]\\ & =\left[\begin{array}{ccc}fy& 0& 0\\ 0& fx& 0\\ -fycx& -fxcy& fxfy\end{array}\right]{\left[\begin{array}{c}{X}_C\\ Y_C\\ 1\end{array}\right]}_{\times }\left[\begin{array}{c}{X}_D\\ Y_D\\ 1\end{array}\right]\\ & =\mathcal{K}(C{}^n\times D{}^n)\\ & =\mathcal{K}\mathbf{n}\end{array}$$

上式表明，直线的线投影只和法向量有关和方向向量无关。

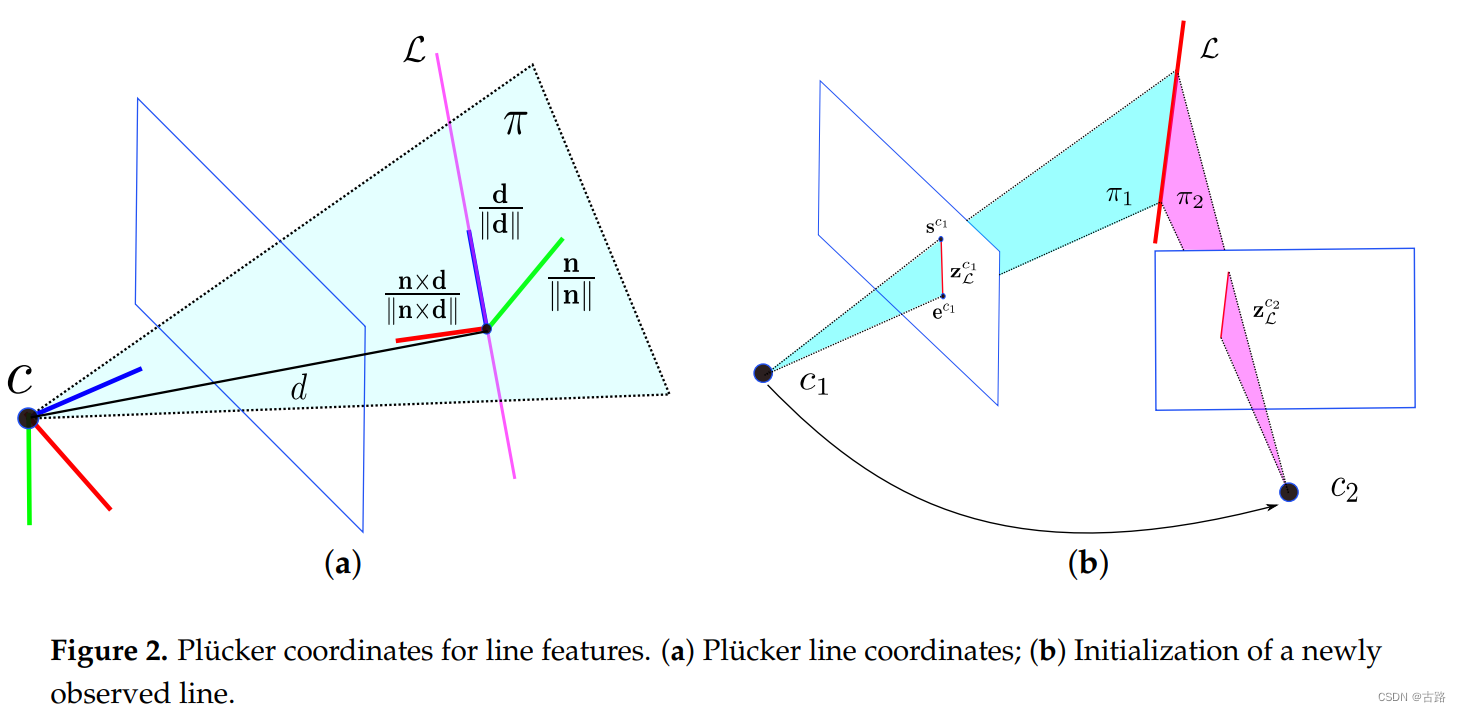
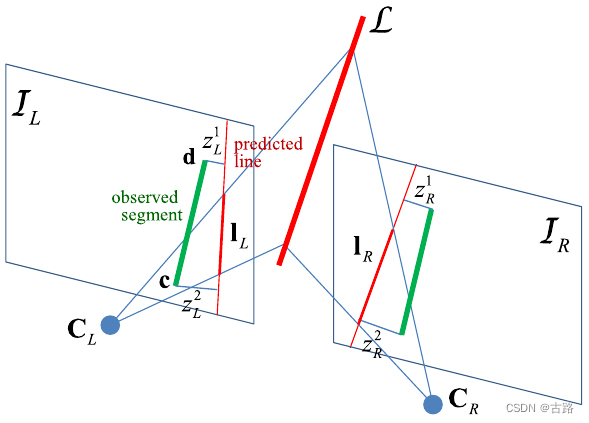
关于投影的误差，我们不可以直接从两幅图像的线段中得到，因为同一条直线在不同图像线段的长度和大小都是不一样的。衡量线的投影误差必须从空间中重投影回当前的图像中才能定义误差。在给定世界坐标系下的空间直线 ${\mathcal{L}}_l^w$ 和正交表示 ${\mathcal{O}}_l$ ，我们首先使用外参（这也是我们需要优化求解的东西） $T_{cw}=\left[\begin{array}{cc}{R}_{cw}& p_{cw}\\ 0& 1\end{array}\right]$ 将直线变换到相机归一化平面下的观测 $c_i$ 坐标下。然后再将直线利用相机内参投影到成像平面上得到投影线段 $l_l^{c_i}$ ，然后我们就得到了线的投影误差。我们将线的投影误差定义为图像中观测线段的端点到从空间重投影回像素平面的预测直线的距离。

线段从世界坐标系转相机归一化平面坐标系（?这一步是怎么做的不是很明白）：
$$\begin{array}{c}\left[\begin{array}{l}{\mathbf{n}}_c\\ {\mathbf{d}}_c\end{array}\right]=\left[\begin{array}{cc}{\mathbf{R}}_{cw}& {\left[{\mathbf{t}}_{cw}\right]}_{\times }{\mathbf{R}}_{cw}\\ 0& {\mathbf{R}}_{cw}\end{array}\right]\left[\begin{array}{l}{\mathbf{n}}_w\\ {\mathbf{d}}_w\end{array}\right]=\left[\begin{array}{cc}{\mathbf{R}}_{wc}^T& {\left[-{\mathbf{R}}_{wc}^T{\mathbf{t}}_{wc}\right]}_{\times }{\mathbf{R}}_{wc}^T\\ 0& {\mathbf{R}}_{wc}^T\end{array}\right]\left[\begin{array}{l}{\mathbf{n}}_w\\ {\mathbf{d}}_w\end{array}\right]\\ =\left[\begin{array}{cc}{\mathbf{R}}_{wc}^T& {\mathbf{R}}_{wc}^T{\left[{\mathbf{t}}_{wc}\right]}_{\times }\\ 0& {\mathbf{R}}_{wc}^T\end{array}\right]\left[\begin{array}{l}{\mathbf{n}}_w\\ {\mathbf{d}}_w\end{array}\right]\end{array}$$

• 最后一步推导用到了一个性质，该性质在李群中比较常见，即：当 $M\in \mathbf{SO}(3)$ 时，有 $[Mu{]}_{\times }=M[u{]}_{\times }{M}^T。$

残差定义：

$$\begin{gathered} {\mathbf{r}}_l\left({\mathbf{z}}_{{\mathcal{L}}_l}^{c_i},\mathcal{X}\right)=\left[\begin{array}{l}d\left({\mathbf{s}}_l^{c_i},{\mathbf{l}}_l^{c_i}\right)\\ d\left({\mathbf{e}}_l^{c_i},{\mathbf{l}}_l^{c_i}\right)\end{array}\right] \\ d(\mathbf{s},1)=\frac{{\mathbf{s}}^{\top }\mathbf{l}}{\sqrt{l_1^2+l_2^2}} \end{gathered}$$

其中 ${\mathbf{s}}_l^{c_i}$ 和 ${\mathbf{e}}_l^{c_i}$ 是图像中观测到的线段端点， ${\mathbf{l}}_l^{c_i}$ 是重投影的预测的直线。

double FeatureManager::reprojection_error( Vector4d obs, Matrix3d Rwc, Vector3d twc, Vector6d line_w ) {

    double error = 0;

    Vector3d n_w, d_w;
    n_w = line_w.head(3);
    d_w = line_w.tail(3);

    Vector3d p1, p2;
    p1 << obs[0], obs[1], 1;
    p2 << obs[2], obs[3], 1;
	// 根据外参将line从世界坐标系转到相机归一化平面坐标系
    Vector6d line_c = plk_from_pose(line_w,Rwc,twc);
    Vector3d nc = line_c.head(3);
    double sql = nc.head(2).norm();
    nc /= sql;

    error += fabs( nc.dot(p1) );
    error += fabs( nc.dot(p2) );
	
    return error / 2.0;
}

这里误差是归一化平面坐标系的误差，因此观测也应该要求是归一化平面，注意中间有个从像素坐标系到归一化平面坐标系的转换，这里没列出来。

误差求解函数在这里。

这个函数实际上只用在了外点剔除这里，真正的优化误差求解是在优化器那里定义的。而且感觉这里的实现坐标有点问题？

4.2.误差雅克比推导

如果要优化的话，需要知道误差的雅克比矩阵：

线特征在VIO下根据链式求导法则：

$${\mathbf{J}}_l=\frac{\partial {\mathbf{r}}_l}{\partial {\mathbf{l}}^{c_i}}\frac{\partial {\mathbf{l}}^{c_i}}{\partial {\mathcal{L}}^{c_i}}\left[\frac{\partial {\mathcal{L}}^{c_i}}{\partial \delta {\mathbf{x}}^i}\frac{\partial {\mathcal{L}}^{c_i}}{\partial {\mathcal{L}}^w}\frac{\partial {\mathcal{L}}^w}{\partial \delta \mathcal{O}}\right]$$

其中第一项 $\frac{\partial {\mathbf{r}}_l}{\partial {\mathbf{l}}^{c_i}}$ ，因为

$$\begin{gathered} {\mathbf{r}}_l=\left[\begin{array}{c}\frac{{\mathbf{s}}^T\mathbf{l}}{\sqrt{l_1^2+l_2^2}}\\ \frac{{\mathbf{e}}^T\mathbf{l}}{\sqrt{l_1^2+l_2^2}}\end{array}\right]=\left[\begin{array}{c}\frac{u_s{l}_1+v_s{l}_2}{\sqrt{l_1^2+l_2^2}}\\ \frac{u_e{l}_1+v_e{l}_2}{\sqrt{l_1^2+l_2^2}}\end{array}\right] \\ \mathbf{s}=\left[\begin{array}{ccc}{u}_s& v_s& 1\end{array}\right] \\ \mathbf{e}=\left[\begin{array}{ccc}{u}_e& v_e& 1\end{array}\right] \\ \mathbf{l}=\left[\begin{array}{ccc}{l}_1& l_2& l_3\end{array}\right] \end{gathered}$$

所以：

$$\begin{array}{rl}\frac{\partial {\mathbf{r}}_l}{\partial \mathbf{l}}& =\left[\begin{array}{lll}\frac{\partial r_1}{\partial l_1}& \frac{\partial r_1}{\partial l_2}& \frac{\partial r_1}{\partial l_3}\\ \frac{\partial r_2}{\partial l_1}& \frac{\partial r_2}{\partial l_2}& \frac{\partial r_2}{\partial l_3}\end{array}\right]\\ & ={\left[\begin{array}{ccc}\frac{-l_1{\mathbf{s}}_l^{\top }\mathbf{l}}{{\left(l_1^2+l_2^2\right)}^{\left(\frac{3}{2}\right)}}+\frac{u_s}{{\left(l_1^2+l_2^2\right)}^{\left(\frac{1}{2}\right)}}& \frac{-l_2{\mathbf{s}}_l^{\top }\mathbf{l}}{{\left(l_1^2+l_2^2\right)}^{\left(\frac{3}{2}\right)}}+\frac{v_s}{{\left(l_1^2+l_2^2\right)}^{\left(\frac{1}{2}\right)}}& \frac{1}{{\left(l_1^2+l_2^2\right)}^{\left(\frac{1}{2}\right)}}\\ \frac{-l_1{\mathbf{e}}_l^{\top }\mathbf{l}}{{\left(l_1^2+l_2^2\right)}^{\left(\frac{3}{2}\right)}}+\frac{e_s}{{\left(l_1^2+l_2^2\right)}^{\left(\frac{1}{2}\right)}}& \frac{-l_2{\mathbf{e}}_l^{\top }\mathbf{l}}{{\left(l_1^2+l_2^2\right)}^{\left(\frac{3}{2}\right)}}+\frac{v_e}{{\left(l_1^2+l_2^2\right)}^{\left(\frac{1}{2}\right)}}& \frac{1}{{\left(l_1^2+l_2^2\right)}^{\left(\frac{1}{2}\right)}}\end{array}\right]}_{2\times 3}\end{array}$$

第二项 $\frac{\partial {\mathbf{l}}^{c_i}}{\partial {\mathcal{L}}^{c_i}}$（像素坐标到相机归一化坐标，相差一个映射矩阵） ，因为

$$\begin{gathered} \mathbf{l}=\mathcal{K}\mathbf{n} \\ \mathcal{L}=\left[\begin{array}{cc}\mathbf{n}& \mathbf{d}\end{array}\right] \end{gathered}$$

所以：

$$\begin{array}{rl}\frac{\partial {\mathrm{l}}^{c_i}}{\partial {\mathcal{L}}_i^{c_i}}& =\left[\begin{array}{cc}\frac{\partial \mathbf{l}}{\mathbf{n}}& \frac{\partial \mathbf{l}}{\mathbf{d}}\end{array}\right]\\ & ={\left[\begin{array}{ll}\mathcal{K}& 0\end{array}\right]}_{3\times 6}\end{array}$$

最后一项矩阵包含两个部分，一个是相机坐标系下线特征对的旋转和平移的误差导数，第二个是直线对正交表示的四个参数增量的导数

第一部分中，

$$\delta {\mathbf{x}}_i=\left[\delta \mathbf{p},\delta \mathbf{\theta },\delta \mathbf{v},\delta {\mathbf{b}}_a^{b_i},\delta {\mathbf{b}}_g^{b_i}\right]$$

在VIO中，如果要计算线特征的重投影误差，需要将在世界坐标系 $w$ 下的线特征变换到IMU坐标系 $b$ 下，再用外参数 ${\mathbf{T}}_{\mathbf{bc}}$ 变换到相机坐标系 $c$ 下。所以

$$\begin{array}{rl}{\mathcal{L}}_c& ={\mathcal{T}}_{bc}^{-1}{\mathcal{T}}_{wb}^{-1}{\mathcal{L}}_w\\ & ={\mathcal{T}}_{bc}^{-1}{\left[\begin{array}{c}{\mathbf{R}}_{wb}^{\top }\left({\mathbf{n}}^w+\left[{\mathbf{d}}^w\right]\times {\mathbf{p}}_{wb}\right)\\ {\mathbf{R}}_{wb}^{\top }{\mathbf{d}}^w\end{array}\right]}_{6\times 1}\end{array}$$

其中
$${\mathcal{T}}_{bc}=\left[\begin{array}{cc}{\mathbf{R}}_{bc}& {\left[{\mathbf{p}}_{bc}\right]}_{\times }{\mathbf{R}}_{bc}\\ 0& {\mathbf{R}}_{bc}\end{array}\right]$$$${\mathcal{T}}_{bc}^{-1}=\left[\begin{array}{cc}{\mathbf{R}}_{\mathbf{bc}}^{\top }& -{\mathbf{R}}_{\mathbf{bc}}^{\top }[{\mathbf{p}}_{\mathbf{bc}}{]}_{\times }\\ 0& {\mathbf{R}}_{\mathbf{bc}}^{\top }\end{array}\right]$$
$$-[a{]}_{\times }b=[b{]}_{\times }a$$
线特征 $\mathcal{L}$ 只优化状态变量中的位移和旋转，所以只需要对位移和旋转求导，其他都是零。下面我们来具体分析旋转和位移的求导。首先是线特征对旋转的求导：

$$\begin{array}{rl}\frac{\partial {\mathcal{L}}_c}{\partial \delta {\theta }_{b{b}^{\prime }}}& ={\mathcal{T}}_{bc}^{-1}\left[\begin{array}{c}\frac{\partial \left(\mathbf{I}-{\left[\delta {\mathbf{\theta }}_{b{b}^{\prime }}\right]}_{\times }\right){\mathbf{R}}_{wb}^{\top }\left({\mathbf{n}}^w+{\left[{\mathbf{d}}^w\right]}_{\times }{\mathbf{p}}_{wb}\right)}{\partial \delta {\mathbf{\theta }}_{b{b}^{\prime }}}]\\ \frac{\partial \left(\mathbf{I}-{\left[\delta {\mathbf{\theta }}_{b{b}^{\prime }}\right]}_{\times }^{\top }\right){\mathbf{R}}_{wb}^{\top }{\mathbf{d}}^w}{\partial \delta {\mathbf{\theta }}_{b{b}^{\prime }}}\end{array}\right]\\ & ={\mathcal{T}}_{bc}^{-1}{\left[\begin{array}{c}{\left[{\mathbf{R}}_{wb}^{\top }\left({\mathbf{n}}^w+{\left[{\mathbf{d}}^w\right]}_{\times }{\mathbf{p}}_{wb}\right)\right]}_{\times }]\\ {\left[{\mathbf{R}}_{wb}^{\top }{\mathbf{d}}^w\right]}_{\times }\end{array}\right]}_{6\times 3}\end{array}$$

然后是线特征对位移的求导：

$$\begin{array}{rl}\frac{\partial {\mathcal{L}}_c}{\partial \delta {\mathbf{p}}_{\mathbf{b}{\mathbf{b}}^{\prime }}}& ={\mathcal{T}}_{bc}^{-1}\left[\begin{array}{c}\frac{\partial {\mathbf{R}}_{wb}^{\top }\left({\mathbf{n}}^w+{\left[{\mathbf{d}}^w\right]}_{\times }\left({\mathbf{p}}_{wb}+\delta {\mathbf{p}}_{b{b}^{\prime }}\right)\right)}{\partial \delta {\mathbf{p}}_{b{b}^{\prime }}}\\ \frac{\partial {\mathbf{R}}_{wb}^{\top }{\mathbf{d}}^w}{\partial \delta {\mathbf{p}}_{b{b}^{\prime }}}\end{array}\right]\\ & ={\mathcal{T}}_{bc}^{-1}{\left[\begin{array}{c}{\mathbf{R}}_{wb}^{\top }{\left[{\mathbf{d}}^w\right]}_{\times }\\ 0\end{array}\right]}_{6\times 3}\end{array}$$

第二部分中 $\frac{\partial {\mathcal{L}}^{c_i}}{\partial {\mathcal{L}}^w}\frac{\partial {\mathcal{L}}^w}{\partial \delta \mathcal{O}}$ ，先解释第一个 $\frac{\partial {\mathcal{L}}^{c_i}}{\partial {\mathcal{L}}^w}$

$${\mathcal{L}}^c={\mathcal{T}}_{wc}^{-1}{\mathcal{L}}^w$$

所以 $\frac{\partial {\mathcal{L}}^{c_i}}{\partial {\mathcal{L}}^w}={\mathcal{T}}_{wc}^{-1}$

然后后面的 $\frac{\partial {\mathcal{L}}^w}{\partial \delta \mathcal{O}}$ 有两种思路，先介绍第一种：

$$\begin{gathered} \frac{\partial {\mathcal{L}}^w}{\partial \delta \mathcal{O}}=\left[\begin{array}{cccc}\frac{\partial {\mathcal{L}}^w}{\partial {\psi }_1}& \frac{\partial {\mathcal{L}}^w}{\partial {\psi }_2}& \frac{\partial {\mathcal{L}}^w}{\partial {\psi }_3}& \frac{\partial {\mathcal{L}}^w}{\partial \varphi }\end{array}\right] \\ \frac{\partial {\mathcal{L}}^w}{\partial {\psi }_1}=\frac{\partial {\mathcal{L}}^w}{\partial \mathbf{U}}\frac{\partial \mathbf{U}}{\partial {\psi }_1} \\ \frac{\partial {\mathcal{L}}^w}{\partial \varphi }=\frac{\partial {\mathcal{L}}^w}{\partial \mathbf{w}}\frac{\partial \mathbf{w}}{\partial {\varphi }_1} \end{gathered}$$

其中 $\mathcal{L}$ 对 $\mathbf{U}$ 和 $\mathbf{w}=[w_1,w_2]$ 求导，因为 ${\mathcal{L}}^w={\left[\begin{array}{cc}{w}_1{\mathbf{u}}_1^{\top }& w_2{\mathbf{u}}_2^{\top }\end{array}\right]}^{\top }$ ，所以

$$\begin{array}{rl}\frac{\partial \mathcal{L}}{\partial \mathbf{U}}& ={\left[\begin{array}{ccc}\frac{\partial \mathcal{L}}{\partial {\mathbf{U}}_1}& \frac{\partial \mathcal{L}}{\partial {\mathbf{U}}_2}& \frac{\partial \mathcal{L}}{\partial {\mathbf{U}}_3}\end{array}\right]}_{6\times 9}\\ & =\left[\begin{array}{ccc}{w}_{1(3\times 3)}& 0& 0\\ 0& w_{2(3\times 3)}& 0\end{array}\right]\end{array}$$

$$\begin{array}{rl}\frac{\partial \mathcal{L}}{\partial \mathbf{w}}& ={\left[\begin{array}{cc}\frac{\partial \mathcal{L}}{\partial w_1}& \frac{\partial \mathcal{L}}{\partial w_2}\end{array}\right]}_{6\times 2}\\ & =\left[\begin{array}{cc}{\mathbf{u}}_1& 0\\ 0& {\mathbf{u}}_2\end{array}\right]\end{array}$$

然后是 $\mathbf{U}$ 对 $\psi$ 和 $\mathbf{W}$ 对 $\varphi$ 的求导，

因为 $\begin{array}{rl}{\mathbf{U}}^{\prime }& \approx \mathbf{U}\left(\mathbf{I}+[\delta \psi {]}_{\times }\right)\end{array}$ ，所以

$$\begin{gathered} {\left[\begin{array}{ccc}{\mathbf{u}}_1& {\mathbf{u}}_2& {\mathbf{u}}_3\end{array}\right]}^{\prime }=\left[\begin{array}{ccc}{\mathbf{u}}_1& {\mathbf{u}}_2& {\mathbf{u}}_3\end{array}\right]+{\left[\begin{array}{ccc}{\mathbf{u}}_1& {\mathbf{u}}_2& {\mathbf{u}}_3\end{array}\right]}_{\times }\delta \psi \\ \frac{{\left[\begin{array}{ccc}{\mathbf{u}}_1& {\mathbf{u}}_2& {\mathbf{u}}_3\end{array}\right]}^{\prime }-\left[\begin{array}{ccc}{\mathbf{u}}_1& {\mathbf{u}}_2& {\mathbf{u}}_3\end{array}\right]}{\delta \psi }={\left[\begin{array}{ccc}{\mathbf{u}}_1& {\mathbf{u}}_2& {\mathbf{u}}_3\end{array}\right]}_{\times } \\ \frac{\partial \mathbf{U}}{\partial {\psi }_1}=\left[\begin{array}{ccc}0& {\mathbf{u}}_3& -{\mathbf{u}}_2\end{array}\right] \\ \frac{\partial \mathbf{U}}{\partial {\psi }_2}=\left[\begin{array}{ccc}-{\mathbf{u}}_3& 0& {\mathbf{u}}_1\end{array}\right] \\ \frac{\partial \mathbf{U}}{\partial {\psi }_1}=\left[\begin{array}{ccc}{\mathbf{u}}_2& -{\mathbf{u}}_1& 0\end{array}\right] \\ \frac{\partial \mathbf{w}}{\partial \varphi }=\left[\begin{array}{c}-w_2\\ w_1\end{array}\right] \end{gathered}$$

所以，可得

$$\begin{array}{rl}\frac{\partial {\mathcal{L}}^w}{\partial \delta \mathcal{O}}& =\left[\begin{array}{cccc}\frac{\partial {\mathcal{L}}^w}{\partial {\psi }_1}& \frac{\partial {\mathcal{L}}^w}{\partial {\psi }_2}& \frac{\partial {\mathcal{L}}^w}{\partial {\psi }_3}& \frac{\partial {\mathcal{L}}^w}{\partial \varphi }\end{array}\right]\\ & =\left[\begin{array}{cccc}\frac{\partial {\mathcal{L}}^w}{\partial \mathbf{U}}\frac{\partial \mathbf{U}}{\partial {\psi }_1}& \frac{\partial {\mathcal{L}}^w}{\partial \mathbf{U}}\frac{\partial \mathbf{U}}{\partial {\psi }_2}& \frac{\partial {\mathcal{L}}^w}{\partial \mathbf{U}}\frac{\partial \mathbf{U}}{\partial {\psi }_3}& \frac{\partial {\mathcal{L}}^w}{\partial \mathbf{w}}\frac{\partial \mathbf{w}}{\partial \varphi }\end{array}\right]\\ & ={\left[\begin{array}{cccc}0& -w_1{\mathbf{u}}_3& w_1{\mathbf{u}}_2& -w_2{\mathbf{u}}_1\\ w_2{\mathbf{u}}_3& 0& -w_2{\mathbf{u}}_1& w_1{\mathbf{u}}_2\end{array}\right]}_{6\times 4}\end{array}$$

---

4.3.误差雅可比求导简洁版(不含imu坐标系转换)

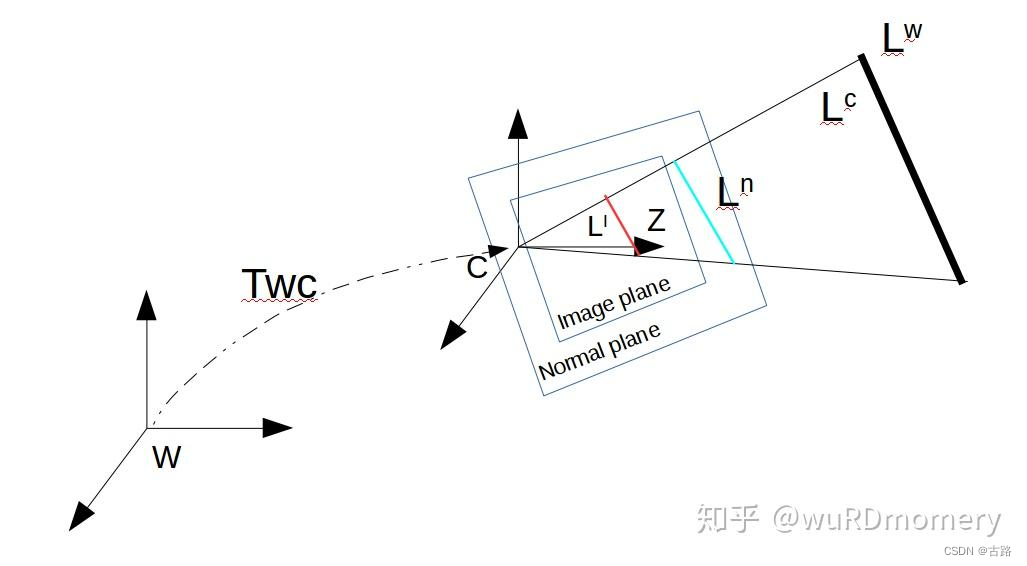
• $L^W$表示在世界坐标系的表示，$L^C$表示在相机坐标系下的表示；
• $L^n$表示归一化平面上的线，$L^I$表示在图像坐标系下的线；

图中的$I_L$表示直线$\mathcal{L}$在图像平面的投影，所以定义误差项为（就是简单的两个点到直线的距离）：

$${\mathbf{r}}_{\mathbf{L}}=\left[\begin{array}{c}{\mathbf{r}}_1\\ {\mathbf{r}}_2\end{array}\right]=\left[\begin{array}{c}\frac{c^{T}I}{\sqrt{l_1^2+l_2^2}}\\ \frac{d^{T}I}{\sqrt{l_1^2+l_2^2}}\end{array}\right]\text{\hspace{1em}(15)}$$

求解Jacobian
跟对3D点的优化问题一样，就是从误差不停的递推到位姿以及直线表示上，用到最最最基本的求导的链式法则：

通用的公式如下：

$$\frac{\partial {\mathbf{r}}_{\mathbf{L}}}{\partial X}=\frac{\partial {\mathbf{r}}_{\mathbf{L}}}{\partial L^I}\frac{\partial L^I}{\partial L^n}\frac{\partial L^n}{\partial L^c}\begin{array}{r}\{\begin{array}{ll}\frac{\partial L^c}{\partial \theta }& \text{ X=}\theta \\ \frac{\partial L^c}{\partial t}& \text{ X=t}\\ \frac{\partial L^c}{\partial L^w}\frac{\partial L^w}{\partial (\theta ,\varphi )}& \text{ X=}{L}^w\end{array}\end{array}\text{\hspace{1em}(16)}$$

先对前面最通用的部分进行求解：

第一部分：

$$\begin{array}{rl}\frac{\partial {\mathbf{r}}_{\mathbf{L}}}{\partial L^I}& =\left[\begin{array}{ccc}\frac{\partial r1}{\partial l_1}& \frac{\partial r1}{\partial l_2}& \frac{\partial r1}{\partial l_3}\\ \frac{\partial r2}{\partial l_1}& \frac{\partial r2}{\partial l_2}& \frac{\partial r2}{\partial l_3}\end{array}\right]\\ & ={\left[\begin{array}{ccc}\frac{-l_1{c}^T{L}^I}{(l_1^2+l_2^2{)}^{\frac{3}{2}}}+\frac{u_c}{(l_1^2+l_2^2{)}^{\frac{1}{2}}}& \frac{-l_2{c}^T{L}^I}{(l_1^2+l_2^2{)}^{\frac{3}{2}}}+\frac{v_c}{(l_1^2+l_2^2{)}^{\frac{1}{2}}}& \frac{1}{(l_1^2+l_2^2{)}^{\frac{1}{2}}}\\ \frac{-l_1{d}^T{L}^I}{(l_1^2+l_2^2{)}^{\frac{3}{2}}}+\frac{u_d}{(l_1^2+l_2^2{)}^{\frac{1}{2}}}& \frac{-l_2{d}^T{L}^I}{(l_1^2+l_2^2{)}^{\frac{3}{2}}}+\frac{v_d}{(l_1^2+l_2^2{)}^{\frac{1}{2}}}& \frac{1}{(l_1^2+l_2^2{)}^{\frac{1}{2}}}\end{array}\right]}_{2\times 3}\end{array}\text{\hspace{1em}(17)}$$

其中：

$l1,l2,l3$表示图像坐标系下直线的三个参数；
$u_c,v_c$表示点$c$的$xy$坐标值，$u_d,v_d$同理；
第二部分：

根据公式（13）可知：

$$\frac{\partial L^I}{\partial L^n}={\mathcal{K}}_{3\times 3}\text{\hspace{1em}(18)}$$

第三部分：

由公式（6）和（13）可知，直线的Plucker表示在归一化平面上只用了其中的法向量部分，因此若有$\mathcal{L}{}^c={\left[\mathbf{n}{}^{\mathbf{c}},\mathbf{d}{}^{\mathbf{c}}\right]}^T$，那么$\mathcal{L}{}^n=\mathbf{n}{}^{\mathbf{c}}$，所以求导有：

$$\frac{\partial L^n}{\partial L^c}={\left[\begin{array}{cc}{\mathbf{I}}_{3\times 3}& 0_{3\times 3}\end{array}\right]}_{3\times 6}\text{\hspace{1em}(19)}$$

第四部分就分这几种情况进行讨论：

对于位姿的姿态部分
根据公式（7）有：

$$\frac{\partial L{}^c}{\partial \theta }=\left[\begin{array}{c}\frac{\partial n_c}{\partial \theta }\\ \frac{\partial d_c}{\partial \theta }\end{array}\right]=\left[\begin{array}{c}\frac{\partial (R_{wc}^T(n_w+[t_{wc}{]}_{\times }{d}_w))}{\partial \theta }\\ \frac{\partial R_{wc}^T{d}_w}{\partial \theta }\end{array}\right]={\left[\begin{array}{c}[R_{wc}^T(n_w+[t_{wc}{]}_{\times }{d}_w){]}_{\times }\\ [R_{wc}^T{d}_w{]}_{\times }\end{array}\right]}_{6\times 3}\text{\hspace{1em}(20)}$$

上述的推导使用了李群的右扰动模型，即$(R_{wc}Exp(\theta ){)}^T=Exp(-\theta )R_{wc}^T$。

对于位姿的位移部分
同样根据公式（7）有：

$$\frac{\partial L{}^c}{\partial t}=\left[\begin{array}{c}\frac{\partial n_c}{\partial t}\\ \frac{\partial d_c}{\partial t}\end{array}\right]=\left[\begin{array}{c}\frac{\partial (R_{wc}^T(n_w+[t_{wc}{]}_{\times }{b}_w))}{\partial t}\\ \frac{\partial R_{wc}^T{b}_w}{\partial t}\end{array}\right]={\left[\begin{array}{c}-R_{wc}^T[b_w{]}_{\times }\\ 0\end{array}\right]}_{6\times 3}\text{\hspace{1em}(21)}$$

对于世界坐标系下直线表示部分
这部分按照公式（16）的步骤，依旧分两个部分：

$\frac{\partial L^c}{\partial L^w}$部分：
$$\frac{\partial L^c}{\partial L^w}=\left[\begin{array}{cc}\frac{\partial {\mathbf{n}}^{\mathbf{C}}}{\partial {\mathbf{n}}^{\mathbf{W}}}& \frac{\partial {\mathbf{n}}^{\mathbf{C}}}{\partial {\mathbf{b}}^{\mathbf{W}}}\\ \frac{\partial {\mathbf{d}}^{\mathbf{C}}}{\partial {\mathbf{n}}^{\mathbf{W}}}& \frac{\partial {\mathbf{d}}^{\mathbf{C}}}{\partial {\mathbf{b}}^{\mathbf{W}}}\end{array}\right]=\left[\begin{array}{cc}{\mathrm{R}}_{wc}^T& {\mathrm{R}}_{wc}^T{\left[{\mathbf{t}}_{wc}\right]}_{\times }\\ 0& {\mathrm{R}}_{wc}^T\end{array}\right]\text{\hspace{1em}(22)}$$
$\frac{\partial L^w}{\partial (\theta ,\varphi )}$部分，这部分其实还可以继续分，如下：
$$\frac{\partial L^w}{\partial (\theta ,\varphi )}=\left[\frac{\partial L^w}{\partial \theta },\frac{\partial L^w}{\partial \varphi }\right]=\left[\frac{\partial L^w}{\partial U}\frac{\partial U}{\partial \theta },\frac{\partial L^w}{\partial W}\frac{\partial W}{\partial \varphi }\right]$$第一部分
$$\begin{array}{rl}\frac{\partial L^w}{\partial U}\frac{\partial U}{\partial \theta }& =\frac{\partial \left[\begin{array}{c}w1{\mathbf{u}}_1\\ w2{\mathbf{u}}_2\end{array}\right]}{\partial [{\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3]}\frac{\partial [{\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3]}{\partial \theta }\\ & ={\left[\begin{array}{ccc}w1& 0& 0\\ 0& w2& 0\end{array}\right]}_{6\times 9}{\left[\begin{array}{ccc}0& -u3& u2\\ u3& 0& -u1\\ -u2& u1& 0\end{array}\right]}_{9\times 3}\\ & ={\left[\begin{array}{ccc}0& -w1u3& w1u2\\ -w2u3& 0& -w2u1\end{array}\right]}_{6\times 3}\end{array}\text{\hspace{1em}(23)}$$ 第二部分
$$\begin{array}{rl}\frac{\partial L^w}{\partial W}\frac{\partial W}{\partial \varphi }& =\frac{\partial \left[\begin{array}{c}w1{\mathbf{u}}_1\\ w2{\mathbf{u}}_2\end{array}\right]}{\partial [w1,w2{]}^T}\frac{\partial [w1,w2{]}^T}{\partial \varphi }\\ & ={\left[\begin{array}{cc}u1& 0\\ 0& u2\end{array}\right]}_{6\times 2}{\left[\begin{array}{c}-w2\\ w1\end{array}\right]}_{2\times 1}\\ & ={\left[\begin{array}{c}-w2u1\\ w1u2\end{array}\right]}_{6\times 1}\end{array}\text{\hspace{1em}(24)}$$ 其中$$w1=cos(\varphi ),w2=sin(\varphi )$$。
两个部分合起来为：
$$\frac{\partial L^w}{\partial (\theta ,\varphi )}={\left[\begin{array}{cc}{\mathrm{R}}_{wc}^T& {\mathrm{R}}_{wc}^T{\left[{\mathbf{t}}_{wc}\right]}_{\times }\\ 0& {\mathrm{R}}_{wc}^T\end{array}\right]}_{6\times 6}{\left[\begin{array}{cccc}0& -w1u3& w1u2& -w2u1\\ -w2u3& 0& -w2u1& w1u2\end{array}\right]}_{6\times 4}\text{\hspace{1em}(25)}$$

最后就是上述推导过程中确实有很多地方向量的notation没有统一，可能有些比较容易混淆，这里确实是因为各个论文的表示不太一样，导致写公式的时候不太一样，自己又偷了个懒，不过该注释的地方都进行了注释。目前比较流行的表示应该是 $L=[\mathbf{n},\mathbf{d}{]}^T$ 或者 $L=[\mathbf{n},\mathbf{v}{]}^T$ ，其中 $\mathbf{n}$ 表示法向量， $\mathbf{d}$ 或者 $\mathbf{v}$ 表示方向向量。

---

4.4.相关代码

优化入口，ceres,主要实现在这里。

• g2o的Jacobian填充参考这里，以及这里的实现。
• ceres的Jacobian填充参考这里

关于线特征的操作，xin同学整理的模块化比较好。