吴恩达机器学习笔记（2）——单变量线性回归（Univariate linear regression）

一、模型描述

上一章已经通过卖房价格的模型简单介绍了什么是回归：我们尝试将变量映射到某一个连续函数上。

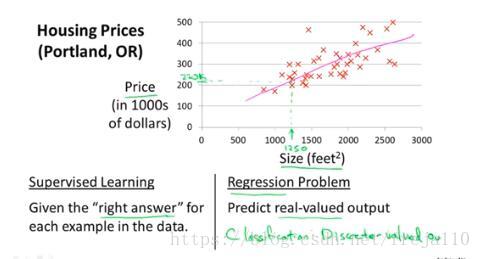
这章我们将这个问题简单地量化为单变量线性回归模型（Univariate linear regression）来理解它。

PS：监督学习最常见的两类问题：
1、回归：预测一个具体的数值输出
2、分类：预测离散值输出

先来看这个过程是如何进行的：

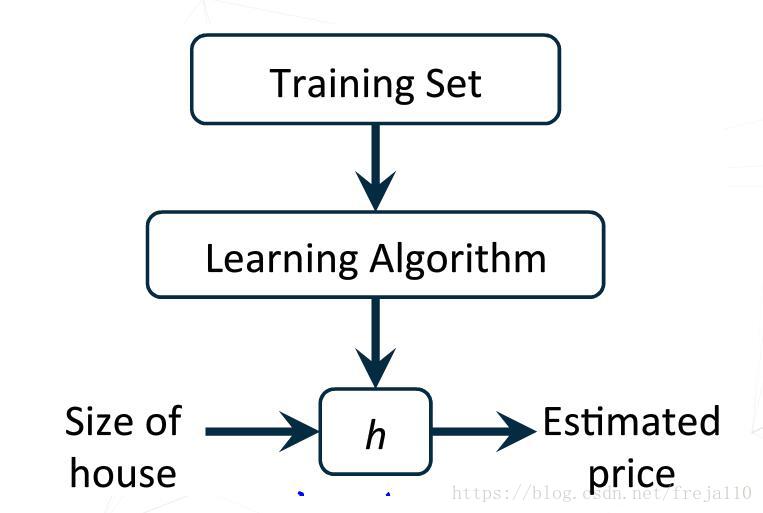
其中，h表示假设函数：

θ是参数，下一节我们谈谈如何选择这两个参数值。

---

---

---

二、代价函数（Cost function）

我们现在有了数据集，并且可以通过改变参数来调整h函数，那么，我们如何定义什么是“更好”的h函数呢？
一般而言，我们通过调整θ，使得所有训练集数据与其拟合数据的差的平方和更小，即认为得到了拟合度更好的函数。

我们引入了代