统计学中的相关概念（不断补充中）p-value,极差等

最新推荐文章于 2024-12-06 22:40:41 发布

morningCV

最新推荐文章于 2024-12-06 22:40:41 发布

阅读量5.8k

点赞数 1

分类专栏：进步

本文链接：https://blog.csdn.net/g_r_c/article/details/8455228

版权

进步专栏收录该内容

19 篇文章

订阅专栏

P值

编辑本段 P值的意义

P value

^[1]

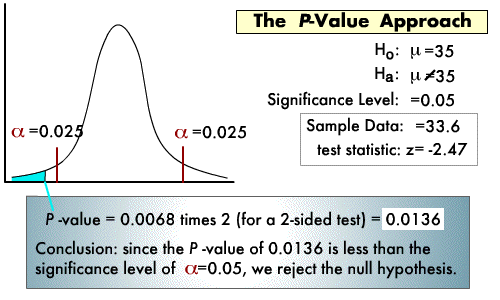
P值（P value）就是当原假设为真时所得到的样本观察结果或更极端结果出现的概率。如果P值很小，说明这种情况的发生的概率很小，而如果出现了，根据小概率原理，我们就有理由拒绝原假设，P值越小，我们拒绝原假设的理由越充分。总之，P值越小，表明结果越显著。但是检验的结果究竟是“显著的”、“中度显著的”还是“高度显著的”需要我们自己根据P值的大小和实际问题来解决。 ^[2]

编辑本段 P值的由来

　　R·A·Fisher（1890-1962）作为一代假设检验理论的创立者，在假设检验中首先提出P值的概念。他认为假设检验是一种程序，研究人员依照这一程序可以对某一总体参数形成一种判断。也就是说，他认为假设检验是数据分析的一种形式，是人们在研究中加入的主观信息。（当时这一观点遭到了Neyman-Pearson的反对，他们认为假设检验是一种方法，决策者在不确定的条件下进行运作，利用这一方法可以在两种可能中作出明确的选择，而同时又要控制错误发生的概率。这两种方法进行长期且痛苦的论战。虽然Fisher的这一观点同样也遭到了现代统计学家的反对，但是他对现代假设检验的发展作出了巨大的贡献。）Fisher的具体做法是：

　　假定某一参数的取值。

　　选择一个检验统计量(例如z 统计量或Z 统计量) ，该统计量的分布在假定的参数取值为真时应该是完全已知的。

　　从研究总体中抽取一个随机样本4计算检验统计量的值5计算概率P值或者说观测的显著水平，即在假设为真时的前提下，检验统计量大于或等于实际观测值的概率。

　　如果P<0.01，说明是较强的判定结果，拒绝假定的参数取值。

　　如果0.01<P值<0.05，说明较弱的判定结果，拒绝假定的参数取值。

　　如果P值>0.05，说明结果更倾向于接受假定的参数取值。

　　因此，随着计算机的发展，P值的计算不再是个难题，使得P值变成最常用的统计指标之一。 ^[2]

^极差

^{极差是指总体各单位的标志值中，最大标志值与最小标志值之差。它是标志值变动的最大范围。极差也称为全距或范围误差，它是测定标志变动的最简单的指标。换句话说，也就是指一组数据中的最大数据与最小数据的差叫做这组数据的极差。极差英文为range ，简写为R，表示为：R=Xmax-Xmin。移动极差（Moving Range）是其中的一种。}

计算公式

　　全距 =最大标志值—最小标志值

　　R=Xmax-Xmin （其中，Xmax为最大值，Xmin为最小值）

　　例如：12 12 13 14 16 21

　　这组数的极差就是：21－12=9

　　方差计算公式：s^2=(1/n)*[(x1-x0)^2 + (x2-x0)^2 +...+ (xn-x0)^2]

　　（X0即为x的平均值）

移动极差

　　移动极差（Moving Range），是指两个或多个连续样本值中最大值与最小值之差，这种差是按这样方式计算的：每当得到一个额外的数据点时，就在样本中加上这个新的点，同时删除其中时间上“最老的”点，然后计算与这点有关的极差，因此每个极差的计算至少与前一个极差的计算共用一个点的值。一般说来，移动极差用于单值控制图，并且通常用两点（连续的点）来计算移动极差。

编辑本段 用途和意义

　　在统计中常用极差来刻画一组数据的离散程度，以及反映的是变量分布的变异范围和离散幅度，在总体中任何两个单位的标准值之差都不能超过极差。同时，它能体现一组数据波动的范围。极差越大，离散程度越大，反之，离散程度越小。

　　极差只指明了测定值的最大离散范围，而未能利用全部测量值的信息，不能细致地反映测量值彼此相符合的程度，极差是总体标准偏差的有偏估计值，当乘以校正系数之后，可以作为总体标准偏差的无偏估计值，它的优点是计算简单，含义直观，运用方便，故在数据统计处理中仍有着相当广泛的应用。但是，它仅仅取决于两个极端值的水平，不能反映其间的变量分布情况，同时易受极端值的影响

编辑本段 残差的特征

　　在回归分析中，测定值与按回归方程预测的值之差，以 δ 表示。残差δ遵从正态分布 N(0，σ2)。（δ-残差的均值）/残差的标准差，称为标准化残差，以δ*表示。δ*遵从标准正态分布 N(0，1)。实验点的标准化残差落在(-2，2)区间以外的概率 ≤0.05。若某一实验点的标准化残差落在(-2，2)区间以外，可在95% 置信度将其判为异常实验点，不参与回归线拟合。

　　显然，有多少对数据，就有多少个残差。残差分析就是通过残差所提供的信息，分析出数据的可靠性、周期性或其它干扰。

所谓残差是指观测值与预测值（拟合值）之间的差，即是实际观察值与回归估计值的差。