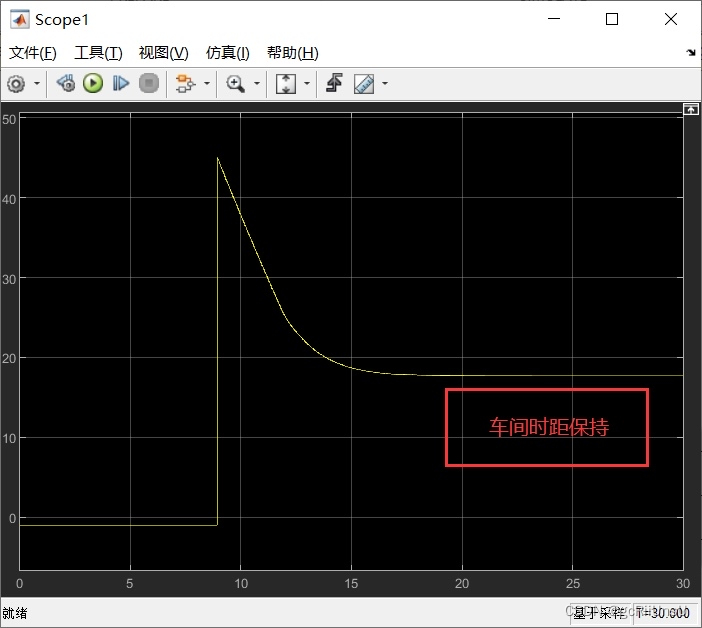
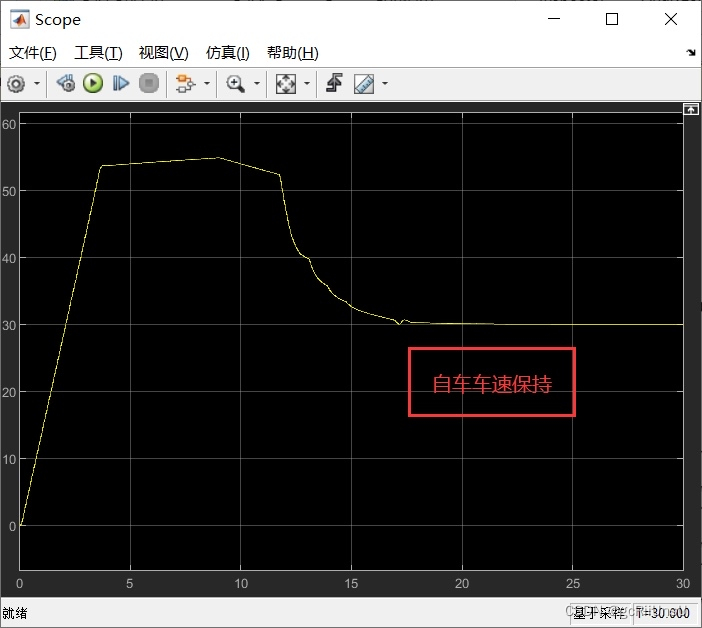
车队控制纵向跟随—CarSim联合simulink仿真自车和前车保持车速一致，车间距保持不变

车队控制纵向跟随—CarSim联合simulink仿真
自车和前车保持车速一致，车间距保持不变
可调整纵向车速、车间距
可自主设置多车辆、多车道
资料内包含.cpar文件、.slx文件，以及cpar文件导入教程
Carsim2019版本，MATLAB需要R2018b及其以上版本

车队控制纵向跟随—CarSim联合Simulink仿真

在现代交通系统中，车队控制是一个重要的研究经验。它可以允许车辆在同一路段上进行自动驾驶，从而确保更加稳定的车辆间距和车速，从而保证交通系统的安全性和流畅性。在此背景下，本文介绍了车队控制中的纵向跟随系统，并利用Carsim和Simulink联合仿真的方法进行了探究。

纵向跟随是指实现车辆的自动化车间距控制系统，该系统通过具备先验知识的算法来控制汽车的纵向运动。本文基于Carsim模拟车辆的运动学和动力学特性，并利用Simulink设计车队控制系统。

在实际的车队管理中，车辆的控制需要考虑多方面因素，例如自车的速度、加速度、距离前车的距离等。针对这些因素，我们可以设定控制器来实现车辆的纵向跟随。在本文中，我们使用了Carsim模拟车队纵向跟随控制逻辑，并实现了多车辆多车道的自主设置。

对于车队纵向跟随系统，最基本的要求是实现车辆间的距离保持不变并且车速一致。因此，在本文中，我们设计了Carsim模拟器来模拟车队的行驶，并使用Simulink仿真来探究纵向跟随控制系统的有效性。

在Carsim和Simulink联合仿真中，我们使用了.cpar和.slx文件，并提供了cpar文件导入教程。在使用中，用户可以自由设置纵向车速和车间距，并且可以自主设置多车辆多车道。将这些要素完美地集成在一起，将可以使车队系统更加完善，从而提高整个交通系统的安全性和流畅性。

注意，为了实现本文中的仿真，Carsim2019版本和MATLAB R2018b及以上版本是必要的前提条件。同时，建议用户在使用本文中提供的仿真器时，按照导入教程进行操作，以保证仿真器的稳定性和可靠性。

在未来，车队控制的研究和应用将会越来越受到重视。本文介绍的Carsim和Simulink联合仿真技术为车队控制系统的研究提供了一种新的思路和方法。希望通过本文的介绍，可以为相关领域的学者和工程师提供一些参考和借鉴。

相关代码,程序地址：http://lanzouw.top/676051087144.html