长期ROI预测技术方案综述

游戏数据科学

已于 2024-11-11 10:37:47 修改

阅读量1.4k

点赞数 22

分类专栏：游戏数据科学文章标签：人工智能深度学习预测用户付费机器学习游戏AI应用

于 2024-10-19 15:52:54 首次发布

本文链接：https://blog.csdn.net/hahoo2009/article/details/143079755

版权

游戏数据科学专栏收录该内容

16 篇文章

订阅专栏

在这里插入图片描述通过对游戏进行长期ROI预测，可以更准确地计算未来的收入和利润，帮助发行投放制定更准确的投放预算和策略，更好地分配资源，优化广告投放的投入，从而实现更高的投资回报。

曲线拟合法

在游戏行业中，曲线拟合算法是比较普遍的一种，以30日ROI预测360日ROI为例，根据历史的前360日的ROI数据得到一个拟合结果，再利用这个拟合结果，根据前30日ROI数据去拟合出未来360日ROI的预测值。常见的曲线拟合算法包括线性回归模型，逻辑回归模型，反正切函数模型，指数函数模型和幂函数模型。

线性回归模型

线性回归模型是一种用于预测因变量（响应变量）与一个或多个自变量（预测变量）之间关系的统计方法。最简单的形式是简单线性回归，其公式见下图，其中，y_是因变量，x是自变量，β0是截距，即当 x=0_x=0 时y的值，β1是自变量的回归系数，表示x每变化一个单位，y的变化量。

$\beta_0 + \beta_1 x$

线性回归模型基于因变量和自变量之间的关系是线性的假设，通常使用最小二乘法估计参数，即通过最小化误差平方和来找到最佳拟合曲线。线性回归模型中的参数，截距和斜率，具有明确的统计意义，便于解释和理解。线性回归的典型曲线见下图：

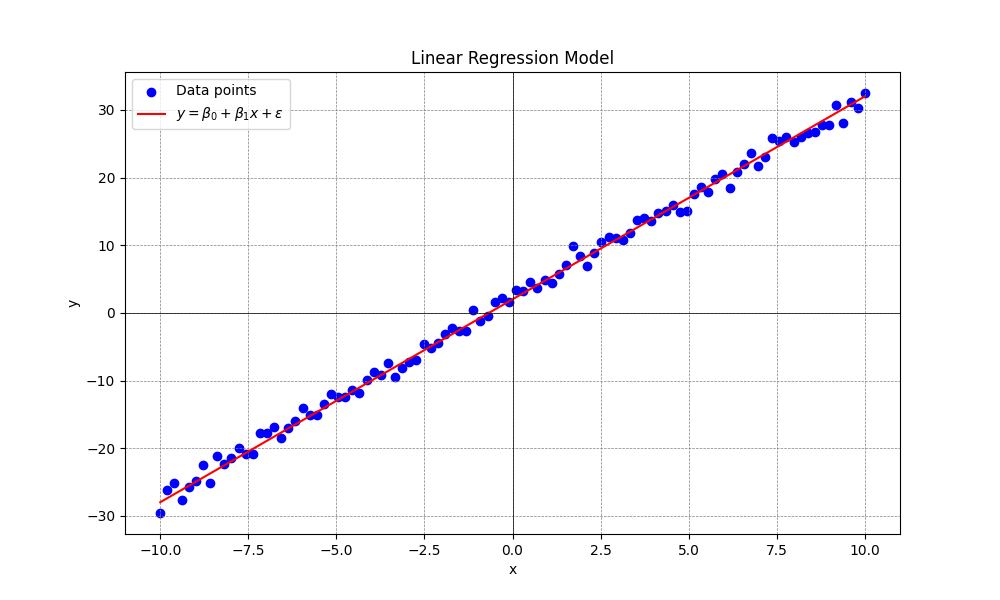
线性回归模型的优点是简单易用，计算方便，并且可解释性强，可以帮助理解变量之间的关系，适合处理各种不同情况的业务场景，能得到广泛应用。但线性回归模型的缺点也很明显，如果变量之间的关系是非线性的，模型效果会较差。同时，线性回归对异常值非常敏感，异常值可能会显著影响模型参数。总的来说，线性回归模型适合作为一个基线模型，提供了一个简单且易于理解的性能基准，帮助评估和比较更复杂模型的性能。

反正切函数模型

反正切函数模型是一种利用反正切函数进行拟合和预测的数学模型。反正切函数是一种常见的非线性函数，具有平滑的S形曲线特性，适用于描述一些非线性关系。其公式见下图，其中，y是输出预测值，x是输入特征，a是垂直缩放因子，b是水平缩放因子，c是幂次因子，arctan⁡是反正切函数。

$\cdot \arctan(bx^c)$

反正切函数模型能够捕捉输入和输出之间的非线性关系，经过缩放和平移等变形处理后，可以拟合类似ROI衰减率的曲线，同时具有平滑的渐进特性，能够较好地描述渐进变化的过程，适用于一些复杂的实际问题。反正切函数的典型曲线见下图：

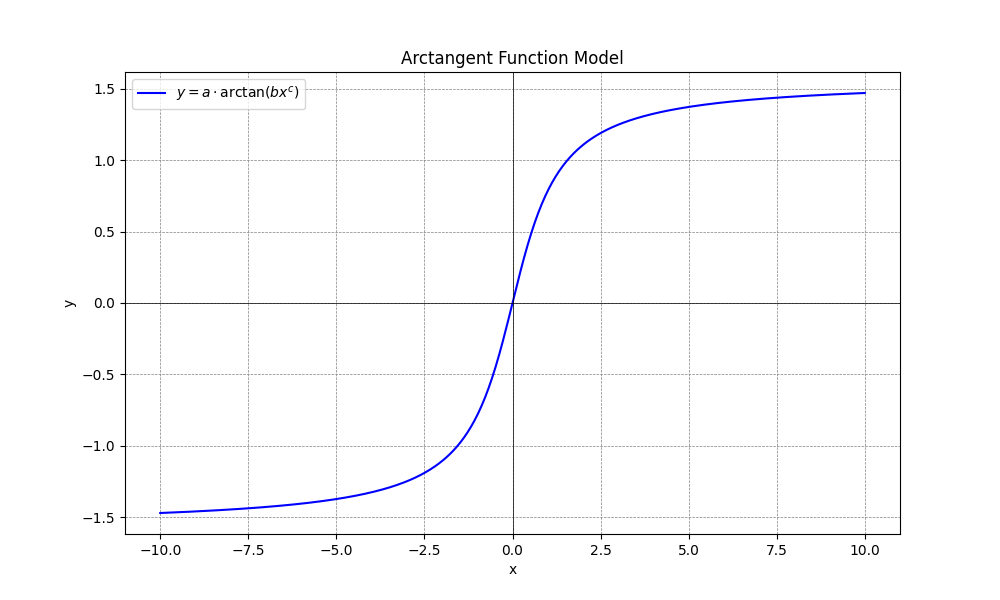
反正切函数模型的优点是生成的曲线平滑，使其在处理一些极限问题时表现良好，能够处理线性模型无法拟合的非线性关系。模型参数a、b、c有一定的物理意义，可以解释特征对输出的影响。反正切函数模型的缺点是在长尾部分经过原点，不太适合ROI衰减趋势中长尾走平的情况。

指数函数模型

指数函数模型是一种常见的数学模型，广泛应用于描述各种业务场景中的指数增长或衰减过程。其公式见下图，其中，y是输出预测值，x是输入特征，a是一个常数，表示当x=0时的初始值，b是衰减速率常数，e是自然对数的底数（约等于2.718）。

$y = ae^{-bx}$

在这个公式中，−bx是指数部分，表示随着x的增加，指数函数的值会按照指数规律衰减，会快速下降到接近于零，但不会等于0。该模型是单调递减的，当 b>0时，随着x增加，y单调递减。指数函数模型的典型曲线见下图：

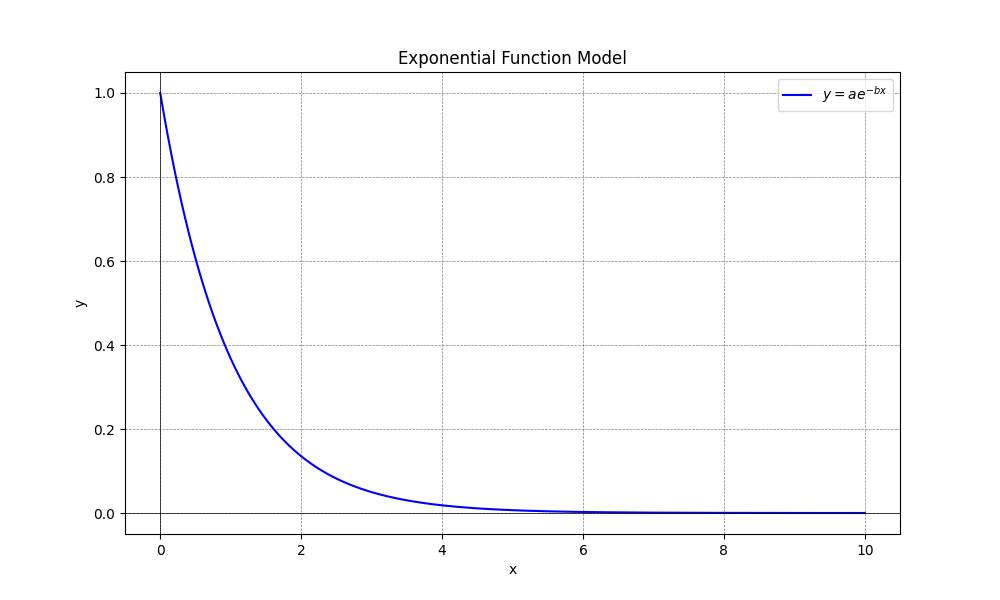
指数函数模型的优点是符合长期ROI单调递减的总体趋势，能比线性回归模型和反正切函数模型更好地拟合长期ROI趋势。但指数函数模型的缺点也很明显，指数级别的增长和衰减速率非常快，y值会快速下降到接近于零，对游戏长期ROI的长尾部分拟合不够准确。

幂函数模型

幂函数是一类重要的数学函数，能够描述许多业务场景中的幂律关系，输出y与输入x之间的关系由x的幂次决定。其公式见下图，其中，y是输出预测值，x是输入特征，a是垂直缩放因子，b是幂指数。

$y = ax^{-b}$

幂函数具有尺度不变性，即如果对x进行尺度变换，输出y也会按照相应的幂次进行变换。由于公式中x的幂次是负的，因此随着x的增加，y会减小，单调递减。通过调整b的值，可以控制输入x对输出y的非线性关系，如果b增大，输入x对输出y的影响会变得更加明显，如果b减小，输入x对输出y的影响会变得更加平缓。幂函数模型的典型曲线见下图：

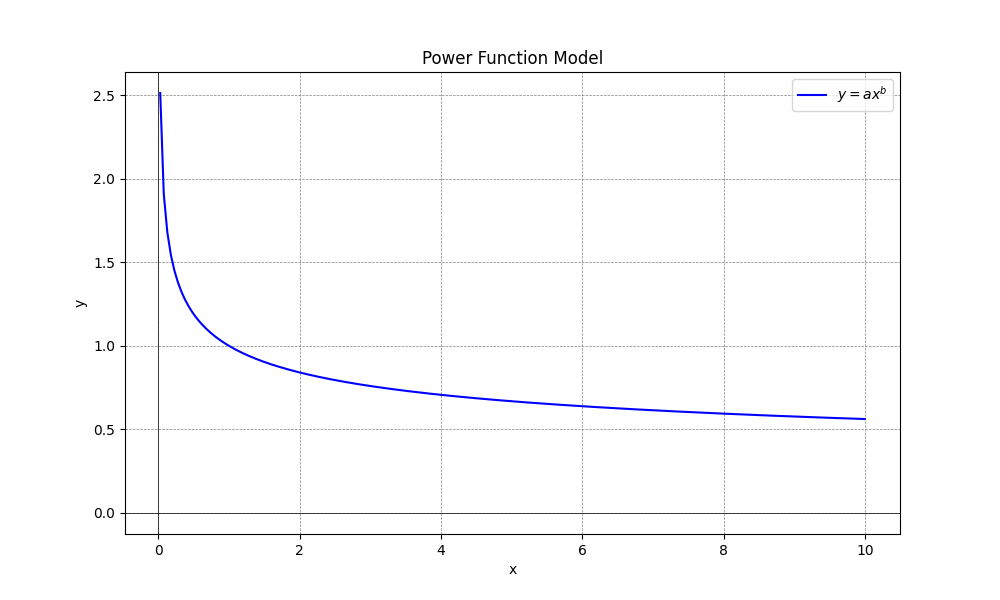
幂函数和指数函数的主要区别在于衰减的速度。根据两个函数的公式，我们可以推导出，如果以每三个月为一个周期，对于指数函数来说，每三个月会以同样的速度衰减：

$\frac{f(9)}{f(6)} = \frac{f(6)}{f(3)} = e ^{-3b}$

而对于幂函数来说，衰减的速度会逐渐放缓，下一个同比例衰减周期会拉长到六个月，即上一个周期的两倍：

$\frac{g(12)}{g(6)} = \frac{g(6)}{g(3)} = 2^{-b}$

所以，幂函数更符合长期ROI的衰减趋势和长尾部分的实际情况。经过在实际业务中的测试，在所有的曲线拟合函数中，幂函数模型的准确率最高。

但幂函数拟合模型也存在一定的问题和不足：

对异常值比较敏感，异常值会影响模型性能。
对数据波动也比较敏感，遇到较大的数据波动情况会导致拟合失败，不能计算出预测值。
对不符合幂律分布的ROI衰减趋势，拟合效果会差一些。
业务上的可解释性不足。

留存 ARPU 拆解法

用另外一种方法，不直接预测ROI，先预测LTV，再根据花费计算ROI，也能得到ROI的预测值，这样就把ROI预测变成了LTV预测。LTV的一种计算公式如图所示，其中，LTV（Lifetime Value）表示客户生命周期价值，是指一个客户在整个生命周期内为游戏带来的净收入，Retained_Users(i)表示第i个时间段的留存用户数，ARPU(i)表示第i个时间段的每用户平均收入（Average Revenue Per User）。对于预测时间段，预测LTV等于每个时间段内的留存用户数和每用户平均收入的乘积再求和，而预测ROI等于预测LTV除以花费。

$Retained_Users(i) × ARPU(i) \text{LTV} = \sum_{i=1}^{t} \text{Retained\textunderscore Users(i)} \times \text{ARPU(i)}$

通常付费留存和ARPPU更加稳定一些，也可以用留存付费用户和ARPPU来计算LTV，公式如图所示，其中，Retained_Pay_Users(i)表示第i个时间段的留存付费用户数，ARPPU(i)表示第i个时间段的每付费用户平均收入（Average Revenue Per Pay User）。实际上是付费留存ARPPU拆解法。

$Retained_Pay_Users(i) × ARPPU(i) \text{LTV} = \sum_{i=1}^{t} \text{Retained\textunderscore Pay\textunderscore Users(i)} \times \text{ARPPU(i)}$

这样，预测问题进一步变成对每个周期内的留存用户数和ARPU的预测，或者对每个周期内的留存付费用户数和ARPPU的预测。下面以第二个公式中的留存付费用户数和ARPPU的预测为例，说明如何进行长期ROI预测。

付费留存预测

长期付费留存变化趋势和长期ROI趋势一样，同样具有随时间单调下降和长尾部分比较平缓的特点，比较符合幂律分布，使用幂函数拟合能得到较好效果。幂函数拟合模型在上面已经介绍，在这里不多展开。通常SLG游戏长期付费留存比较稳定，可以认为付费留存部分的预测误差较小。

ARPPU预测

付费留存ARPPU拆解法的技术难点在于ARPPU的预测。不同游戏，不同国家，不同渠道用户的 ARPPU 表现差异很大，需要结合实际业务场景进行算法选择。

如果游戏新增付费用户的 ARPPU 非常稳定，可以采用已有ARPPU 历史数据的平均值来简单代替未来的 ARPPU 值，得到的计算公式如图所示：

$Retained_Pay_Users ( i ) × ARPPU_AVG ( i ) \text{LTV} = \sum_{i=1}^{t} \text{Retained\textunderscore Pay\textunderscore Users}(i) \times \text{ARPPU\textunderscore AVG}(i)$

但实际预测不能简单采用平均值，需要根据游戏业务的实际ARPPU趋势和分布来选择合适的预测模型。举个例子，如果ARPPU也符合幂律分布，可以使用幂函数拟合。如果存在其他规律，需要先分析其规律，再选择合适的模型。

实际ARPPU预测还需要考虑到付费模型和运营活动。为了能够更加准确地预测具有波动性的ARPPU，需要与产品和运营同学合作，利用产品和运营的业务知识，对ARPPU的拟合进行相应修正。

用户分群付费预测

更进一步，对于付费留存ARPPU拆解法，要想对分月ARPPU预测得更加准确，考虑到数量较少的大R用户可能会对ARPPU产生波动影响，一个思路是将留存付费用户进一步分群，比如按付费金额来分，分为小R用户，中R用户，大R用户等，分别计算每一个分群的付费留存和ARPPU，得到每一个分群的LTV，再求和得到总LTV。用户分群既可以按照付费金额分群，也可以按照国家，等级，行为特征等各种不同策略来分群。具体分群操作可以根据经验来做，也可以使用机器学习算法来做，比如K-Means聚类算法。K-Means聚类算法是一种常用的无监督学习算法，旨在将数据集划分为K个簇，使得每个簇内的数据点尽可能相似，而不同簇之间的数据点尽可能不同。

用户付费预测

另一个思路是在用户层级进行LTV预测，即对每一个用户，预测该用户在预测时间段内的付费金额，再把所有用户的付费金额加起来，得到总LTV。通常使用机器学习和深度学习模型来预测用户付费金额，之前对常见的预测模型和方法做了总结，参见游戏用户生命周期价值预测模型综述。

与时间序列模型的结合

不管是曲线拟合法，还是留存ARPU拆解法，都没有考虑因为时间周期特征，比如节日，季节等因素而引起的LTV和ROI变化，以及市场行情变化。所以考虑引入时间序列模型，将曲线拟合法和留存ARPU拆解法与时间序列模型结合，既能根据ROI，留存和ARPU等数据的长期趋势来预测，也能更准确反应出时间周期上的变化趋势。目前市场上常见的时间序列模型有谷歌的TimesFM，AWS的GluonTS，FaceBook的Prophet，Nixtla的TimeGPT等，具体选用哪个需要结合业务需求和模型测试效果。