转自zhiyong_will http://blog.csdn.net/google19890102/article/details/18222103
一、极限学习机的概念
极限学习机(Extreme Learning Machine) ELM,是由黄广斌提出来的求解单隐层神经网络的算法。
ELM最大的特点是对于传统的神经网络,尤其是单隐层前馈神经网络(SLFNs),在保证学习精度的前提下比传统的学习算法速度更快。
二、极限学习机的原理
ELM是一种新型的快速学习算法,对于单隐层神经网络,ELM 可以随机初始化输入权重和偏置并得到相应的输出权重。
(选自黄广斌老师的PPT)
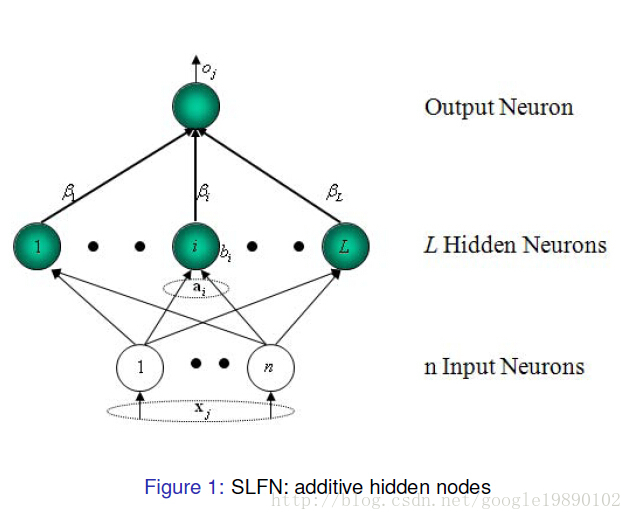
对于一个单隐层神经网络(见Figure 1),假设有个任意的样本
,其中
,
。对于一个有
个隐层节点的单隐层神经网络可以表示为
其中,为激活函数,
为输入权重,
为输出权重,
是第
个隐层单元的偏置。
表示
和
的内积。
单隐层神经网络学习的目标是使得输出的误差最小,可以表示为
即存在,
和
,使得
可以矩阵表示为
其中,是隐层节点的输出,
为输出权重,
为期望输出。
,
为了能够训练单隐层神经网络,我们希望得到,
和
,使得
其中,,这等价于最小化损失函数
传统的一些基于梯度下降法的算法,可以用来求解这样的问题,但是基本的基于梯度的学习算法需要在迭代的过程中调整所有参数。而在ELM算法中, 一旦输入权重和隐层的偏置
被随机确定,隐层的输出矩阵
就被唯一确定。训练单隐层神经网络可以转化为求解一个线性系统
。并且输出权重
可以被确定
其中,是矩阵
的Moore-Penrose广义逆。且可证明求得的解
的范数是最小的并且唯一。
三、实验
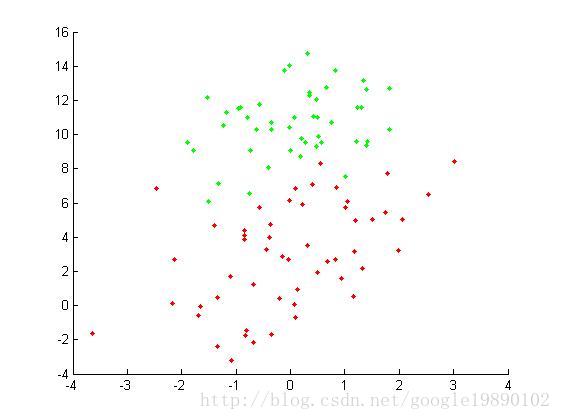
激活函数
























 6310
6310

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








