基于Ziegler-Nichols和IAE算法的PID控制器kp,ki,kd参数计算matlab仿真

目录

1.课题概述

2.系统仿真结果

3.核心程序与模型

4.系统原理简介

4.1Ziegler-Nichols方法

4.2 IAE（积分绝对误差）方法

5.完整工程文件

---

1.课题概述

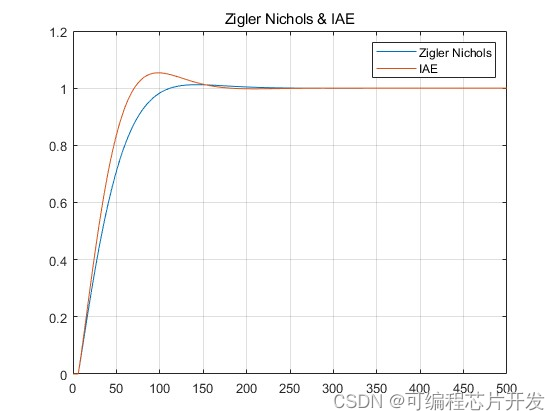
         分别通过Ziegler-Nichols和IAE算法，对PID控制器参数kp，ki，kd进行参数整定，最后对比两种算法得到的PID控制器的性能。

2.系统仿真结果

3.核心程序与模型

版本：MATLAB2022a

................................................................
%初始时间间隔  
Ts    = 1;
% 时间常数  
T0     = 5;
%最大加速度  
at     = 1;
%最大时间
fmax   = 500;
%初始误差  
errs = 0;
%时间常数  
tao    = 25;
%比例系数  
kp     = 1.747;
%分子  
num    = kp;
%分母  
den    = [tao 1];

%Zigler Nichols
%比例增益
Kp1    = (tao/(kp*T0));% 第1比例增益 
Kp2    = ((0.9*tao)/(kp*T0))*0.1; % 第2比例增益 
Kp3    = ((1.2*tao)/(kp*T0))*0.1;% 第3比例增益 
%积分
Ki2    = 3.33*T0;
Ki3    = 2*T0;
%微分
Kd3    = 0.5*T0; 
%调用Simulink模型
sim('Model2.slx');

%画图
r    = Tout.signals(1).values;% 参考输入
p1   = Tout.signals(3).values;% p值
pi1  = Tout.signals(4).values;% pi值
pid1 = Tout.signals(5).values;% pid值

figure;
plot(tout,r,'LineWidth',2);
hold on
plot(tout,p1);
hold on
plot(tout,pi1);
hold on
plot(tout,pid1);
hold on

title('Zigler Nichols计算控制参数后的PID控制器性能')
legend('参考输入','p输出','pi输出','pid输出');
grid;

save R1.mat
0002

4.系统原理简介

       在控制系统设计中，PID（比例-积分-微分）控制器是一种广泛使用的控制策略。PID控制器通过调整系统的偏差，以达到所需的输出。它由三个主要部分组成：比例（P）、积分（I）和微分（D）部分。

Ziegler-Nichols和IAE（积分绝对误差）是两种常用的PID参数整定方法。

4.1Ziegler-Nichols方法

      Ziegler-Nichols方法是基于实验和观察的方法，它提供了如何选择PID控制器的参数的指导。该方法基于系统对阶跃输入的响应来计算参数。

a. 比例增益（kp）：选择一个较小的初始比例增益，并观察系统的响应。如果系统的输出没有达到期望的输出，则增加kp的值。如果系统的输出超出了期望的输出，则减少kp的值。重复这个过程，直到找到使系统输出接近期望输出的kp值。

b. 积分增益（ki）：一旦选择了kp，可以通过以下公式选择ki：ki = kp / (T1 * e)，其中T1是时间常数（T1 = 0.5秒），e是期望的输出与实际输出之间的误差。

c. 微分增益（kd）：选择ki后，可以通过以下公式选择kd：kd = (kp * Td) / T2，其中Td是微分时间常数（Td = 0.1秒），T2是积分时间常数（T2 = 0.5秒）。

       Ziegler-Nichols方法的优点是它基于实验数据，因此可以直接应用于特定的系统。然而，它需要多次调整参数，并且可能不适用于所有类型的系统。

4.2 IAE（积分绝对误差）方法

      IAE方法是基于一种特定的性能指标来选择PID控制器的参数。该方法的目标是使系统的输出跟踪期望的输出，同时使积分绝对误差的积分值最小化。

a. 比例增益（kp）：首先选择一个较小的初始比例增益，并观察系统的响应。如果系统的输出没有达到期望的输出，则增加kp的值。如果系统的输出超出了期望的输出，则减少kp的值。重复这个过程，直到找到使系统输出接近期望输出的kp值。

b. 积分增益（ki）：一旦选择了kp，可以通过以下公式选择ki：ki = kp * (t / (e - L))，其中t是时间常数（t = 0.5秒），e是期望的输出与实际输出之间的误差，L是积分下限（L = 0）。这个公式是基于IAE方法的理论推导得出的。

c. 微分增益（kd）：选择ki后，可以通过以下公式选择kd：kd = kp * (t / (e - L)) * sqrt(e)，其中sqrt(e)是e的平方根。这个公式也是基于IAE方法的理论推导得出的。

       IAE方法的优点是它有一个明确的目标函数，因此可以更容易地应用于不同类型的系统。此外，它只需要调整少量的参数，因此可以更快地找到合适的参数值。然而，它可能需要更复杂的数学计算，因此可能需要更多的计算资源。

5.完整工程文件

v

v