卷积神经网络的深入理解-评测指标篇（PR曲线，ROC曲线，AUC面积，IOU，AP含实例）

    2023.1.10：补充多分类的准确率/召回率/精确度/
                        F1-score的计算
    (变化的部分会以红色字体标出)

绪论

这一篇主要是介绍一下模型的评测指标，与上几篇文章一样都会持续更新。

什么是评测指标？

评测指标是用来定量衡量模型的性能的，是作为各种方法比较的一个标准。
评测指标可以分为分类任务的评测指标和回归任务的评测指标
下面会详细介绍两种任务的评测指标。

分类任务评测指标

1、准确率/召回率/精确度/F1-score

（1）二分类

在这之前我们要了解几个概念：

*	正例（预测）	反例（预测）
正例（真实情况）	TP（真正例（true positive）预测为正，真实情况为正时）	FN（假反例（false negative）预测为反，真实情况为正时）
反例（真实情况）	FP（假正例（false positive）预测为正，真实情况为反时）	TN（真反例（true negative）预测为反，真实情况为反）

准确率（Accuracy）（绝不能冤枉一个好人）：
$$Accuracy=\frac{(TP+TN)}{(TP+FP+TN+FN)}=\frac{预测正确的样本数}{总的样本数}$$
精确度（Precision）（注意这里正反是相对的）：
$$Precision=\frac{TP}{TP+FP}=\frac{预测正确的正样本数}{预测为正的样本数}$$
或
$$Precision=\frac{TN}{FN+TN}=\frac{预测正确的负样本数}{预测为负的样本数}$$
本质上是一样的，只不过一般选择正样本（也就是你关注的样本）计算精确度。
召回率（Recall）（与精确度一样，只选择正样本计算召回率）（宁错杀一千也不能放过一个）：
$$Recall=\frac{TP}{TP+FN}=\frac{预测正确的正样本数}{真实标签为正的样本数}$$
即正样本有多少被召回。
F1-score（综合Precision和Recall的评估）：
$$F1score=\frac{2\ast Precision\ast Recall}{Precision+Recall}$$

（2）多分类

参考自：多分类模型Accuracy, Precision, Recall和F1-score的超级无敌深入探讨
如下混淆矩阵：

*	🐱（预测）	🐕（预测）	🐏（预测）
🐱（真实）	40	20	10
🐕（真实）	35	85	40
🐏（真实）	0	10	20

准确率（Accuracy）：
$$Accuracy=\frac{预测正确的样本数}{总的样本数}=\frac{40+85+20}{75+115+70}=\frac{29}{52}$$
特殊情况（类别数量差异过大）准确率难以评估模型的好坏，比如：
🐱，🐕，🐏的数量分别为91，7，2，若模型将输入的图片都预测为🐱，则准确率为91%，这显然不能准确评估模型的性能好坏。

🐱，🐕，🐏的精确度Precision和召回率Recall如下：
$$Precision🐱=\frac{预测🐱正确的样本数}{预测为🐱的样本个数}=\frac{40}{40+35}=\frac{8}{15}$$
$$Precision🐕=\frac{预测🐕正确的样本数}{预测为🐕的样本个数}=\frac{85}{85+30}=\frac{17}{23}$$
$$Precision🐏=\frac{预测🐏正确的样本数}{预测为🐏的样本个数}=\frac{20}{20+50}=\frac{2}{7}$$
$$Recall🐱=\frac{预测🐱正确的样本数}{真实的🐱的样本个数}=\frac{40}{40+30}=\frac{4}{7}$$
$$Recall🐕=\frac{预测🐕正确的样本数}{真实的🐕的样本个数}=\frac{85}{85+75}=\frac{17}{32}$$
$$Recall🐏=\frac{预测🐏正确的样本数}{真实的🐏的样本个数}=\frac{20}{20+10}=\frac{2}{3}$$
如果想评估整个模型的准确程度，必须考虑🐱，🐕，🐏三个类别的综合预测性能。那么，到底要怎么综合这三个类别的Precision呢？有如下几种解决方案：

Macro-average方法

将不同类别的评估指标（Precision/ Recall/ F1-score）加起来求平均，其值显然受稀有类别的影响。
$$Macro-Precision=\frac{Precision🐱+Precision🐕+Precision🐏}{3}=0.5194$$
$$Macro-Recall=\frac{Recall🐱+Recall🐕+Recall🐏}{3}=0.5898$$

Weighted-average方法

该方法给不同类别不同权重（权重根据该类别的真实分布比例确定）考虑到了类别不平衡的情况。
$$W🐱：W🐕：W🐏=\frac{7}{26}：\frac{16}{26}：\frac{3}{26}$$
$$Weighted-Precision=W🐱\ast P🐱+W🐕\ast P🐕+W🐏\ast P🐏=0.6314$$
$$Weighted-Recall=W🐱\ast R🐱+W🐕\ast R🐕+W🐏\ast R🐏=0.5577$$

Micro-average方法

和上面那个计算准确率的方法一样
$$Micro-Precision=\frac{预测正确的样本数}{预测的总样本数}=\frac{40+85+20}{75+115+70}=\frac{29}{52}=0.5577$$
$$Micro-Recall=\frac{预测正确的样本数}{真实的总样本数}=\frac{40+85+20}{70+160+30}=\frac{29}{52}=0.5577$$
可见Micro-Precision等于Micro-Recall等于Accuracy
$$F1score=\frac{2\ast Precision\ast Recall}{Precision+Recall}=0.5577$$
最后得到：
$Micro-Precision=Micro-Recall=Accuracy=F1score$

2、Precision/Recall（P-R）曲线

Precision/Recall曲线也叫做P-R曲线，Precision与Recall是一对矛盾的变量，考虑到类别不平衡的情况。

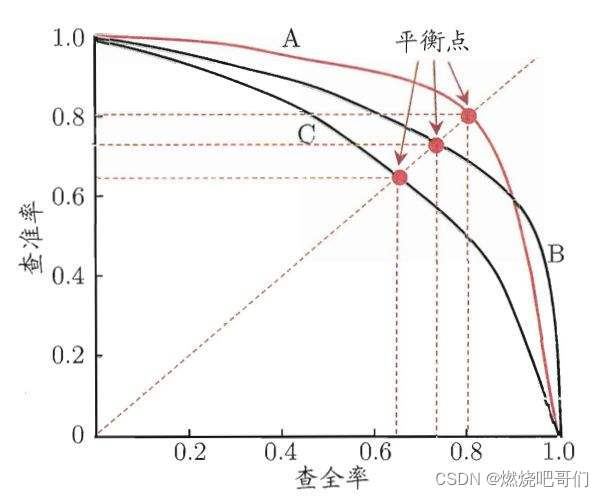
从图中可以看出（上图中查全率即为召回率，查准率即为精确度）：
1、召回率增加，精度下降；

下面以我的角度解释一下为什么查全率与查准率的关系成反比。
通俗一点就是
重查全率(recall): 宁可错杀一千，不可漏过一个。
重查准率(precision): 宁可漏过坏人，不可错杀无辜的好人。

首先我们假设正例样本数（T）和反例样本数（F）是确定的。
即：
$TP+FN=T(实际正样本的总个数)$
$FP+TN=F(实际负样本的总个数)$
假设我们要提高查全率
$$R=\frac{TP}{(TP+FN)}=\frac{TP}{T}$$
$T$的数量是不变的，要提高查全率我们就要提高$TP$即预测为正的个数，而
$$P=\frac{TP}{(TP+FP)}$$
$TP$的提高，必然会增加预测正例$TP+FP$，此过程中会引入新增的FP，
且分母$(TP+FP)$的增幅会大于分子$TP$的增幅。

2、曲线与坐标值面积越大，性能越好（能更大的提升精确度和召回率）；但是有时面积不好计较，那么就选择$y=x$与P-R曲线的交点也叫作平衡点（BEP）比较BEP，越大的学习器越优。
3、对正负样本不均衡问题较敏感。

3、ROC曲线

ROC曲线的横坐标是false positive rate（FPR）：
$$FPR=\frac{FP}{(FP+TN)}=\frac{将反例预测为正例的样本数}{标签为反的样本数}$$
纵坐标为true positive rate（TPR）
$$TPR=\frac{TP}{(TP+FN)}=\frac{将正例预测为正例的样本数}{标签为正的样本数}$$
下图来自阿里公开课

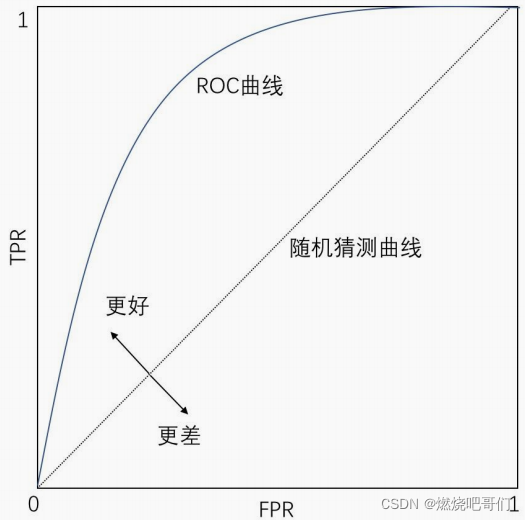
ROC曲线对正负样本不均衡问题不敏感。

那么该选择PR曲线还是ROC曲线呢？

这里引用了这篇博客P-R曲线及与ROC曲线区别
1、在很多实际问题中，正负样本数量往往很不均衡。比如，计算广告领域经常涉及转化率模型，正样本的数量往往是负样本数量的1/1000，甚至1/10000。若选择不同的测试集，P-R曲线的变化就会非常大，而ROC曲线则能够更加稳定地反映模型本身的好坏。所以，ROC曲线的适用场景更多，被广泛用于排序、推荐、广告等领域。
2、但需要注意的是，选择P-R曲线还是ROC曲线是因实际问题而异的，如果研究者希望更多地看到模型在特定数据集上的表现，P-R曲线则能够更直观地反映其性能。
3、ROC兼顾了正负样本。当正负样本比例失调时，比如正样本1个，负样本100个，则ROC曲线变化不大，此时用PR曲线更加能反映出分类器性能的好坏。

4、AUC面积

AUC面积其实就是ROC曲线的下半部分面积，与P-R图类似，通过比较AUC面积来比较学习器的优劣，面积大的更优。

回归任务评测指标

1、IOU（Intersection-over-Union）交并比

IOU多用于检测、分割任务中
$$IOU=\frac{A\cap B}{A\cup B}$$

2、AP（Average Precision）含计算实例

如图所示20个样本的id，预测概率，以及标签。

id	Score	Label	id	Score	Label
1	0.23	0	11	0.03	0
2	0.76	1	12	0.09	0
3	0.01	0	13	0.65	0
4	0.91	1	14	0.07	0
5	0.13	0	15	0.12	0
6	0.45	0	16	0.24	1
7	0.12	1	17	0.1	0
8	0.03	0	18	0.23	0
9	0.38	1	19	0.46	0
10	0.11	0	20	0.08	1

对上述标签进行概率排序

id	Score	Label	id	Score	Label
4	0.91	1	7	0.12	1
2	0.76	1	15	0.12	0
13	0.65	0	10	0.11	0
19	0.46	0	17	0.1	0
6	0.45	0	12	0.09	0
9	0.38	1	20	0.08	1
16	0.24	1	14	0.07	0
1	0.23	0	8	0.03	0
18	0.23	0	11	0.03	0
5	0.13	0	3	0.01	0

正样本的id为：
2、4、7、9、16、20一共六个
top-N就是取前N个，注意是将这N个都预测为正
比如top-5就是取前5个(上面表格中加粗的部分)
$$Precision=\frac{TP}{TP+FP}=\frac{预测正确的正样本数}{预测为正的样本数}=\frac{2}{5}$$
$$Recall=\frac{TP}{TP+FN}=\frac{预测正确的正样本数}{真实标签为正的样本数}=\frac{2}{6}$$
(1)下面是top-1到top-20的表格：

top-N	Precision(注意这里是精确度)	recall
1	1/1	1/6
2	2/2	2/6
3	2/3	2/6
4	2/4	2/6
5	2/5	2/6
6	3/6	3/6
7	4/7	4/6
8	4/8	4/6
9	4/9	4/6
10	4/10	4/6
11	5/11	5/6
12	5/12	5/6
13	5/13	5/6
14	5/14	5/6
15	5/15	5/6
16	6 /16	6/6
17	6/17	6/6
18	6/18	6/6
19	6/19	6/6
20	6/20	6/6

上面表格中大字号黑体的精确度是相同召回率的最大值。

(2)设置阈值统计recall大于等于每个阈值时最大的精确度
这里取11个阈值[0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1]
阈值为0时，recall全部大于0，从中取出最大精确度：
$$P=max\left\{\frac{1}{1},\frac{2}{2},\frac{3}{6},\frac{4}{7},\frac{5}{11},\frac{6}{16}\right\}=1$$
阈值为0.1时，recall全部大于等于0.1，从中选出最大精确度：
$$P=max\left\{\frac{1}{1},\frac{2}{2},\frac{3}{6},\frac{4}{7},\frac{5}{11},\frac{6}{16}\right\}=1$$
阈值为0.2时，recall大于等于0.2的值有$\frac{2}{6}$,$\frac{3}{6}$,$\frac{4}{6}$,$\frac{5}{6}$,$\frac{6}{6}$,
$$P=max\left\{\frac{2}{2},\frac{3}{6},\frac{4}{7},\frac{5}{11},\frac{6}{16}\right\}=1$$
阈值为0.3时recall大于等于0.3的值有$\frac{2}{6}$,$\frac{3}{6}$,$\frac{4}{6}$,$\frac{5}{6}$,$\frac{6}{6}$,
$$P=max\left\{\frac{2}{2},\frac{3}{6},\frac{4}{7},\frac{5}{11},\frac{6}{16}\right\}=1$$
阈值为0.4时recall大于等于0.4的值有$\frac{3}{6}$,$\frac{4}{6}$,$\frac{5}{6}$,$\frac{6}{6}$,
$$P=max\left\{\frac{3}{6},\frac{4}{7},\frac{5}{11},\frac{6}{16}\right\}=\frac{4}{7}$$
阈值为0.5时recall大于等于0.5的值有$\frac{3}{6}$,$\frac{4}{6}$,$\frac{5}{6}$,$\frac{6}{6}$,
$$P=max\left\{\frac{3}{6},\frac{4}{7},\frac{5}{11},\frac{6}{16}\right\}=\frac{4}{7}$$
阈值为0.6时recall大于等于0.6的值有$\frac{3}{6}$,$\frac{4}{6}$,$\frac{5}{6}$,$\frac{6}{6}$,
$$P=max\left\{\frac{4}{7},\frac{5}{11},\frac{6}{16}\right\}=\frac{4}{7}$$
阈值为0.7时recall大于等于0.7的值有$\frac{5}{6}$,$\frac{6}{6}$,
$$P=max\left\{\frac{5}{11},\frac{6}{16}\right\}=\frac{5}{11}$$
阈值为0.8时recall大于等于0.8的值有$\frac{5}{6}$,$\frac{6}{6}$,
$$P=max\left\{\frac{5}{11},\frac{6}{16}\right\}=\frac{5}{11}$$
阈值为0.9时recall大于等于0.9的值有$\frac{6}{6}$,
$$P=max\left\{\frac{6}{16}\right\}=\frac{6}{16}$$
阈值为1时recall大于等于1的值有$\frac{6}{6}$,
$$P=max\left\{\frac{6}{16}\right\}=\frac{6}{16}$$
(3)计算AP值(AP值就是上述11个精确度的平均值)：
$$AP=\frac{1+1+1+1+\frac{4}{7}+\frac{4}{7}+\frac{4}{7}+\frac{5}{11}+\frac{5}{11}+\frac{6}{16}+\frac{6}{16}}{11}$$
(4)mAP值就是各个类别的平均值。