1. 问题导入——微分学的产生背景(解决瞬时速度、加速度、曲线切线等相关问题)

2. 微积分是微分学和积分学的总称,由牛顿和莱布尼兹在研究物理和几何问题的过程中,总结前人的经验,于十七世纪后期建立起来的

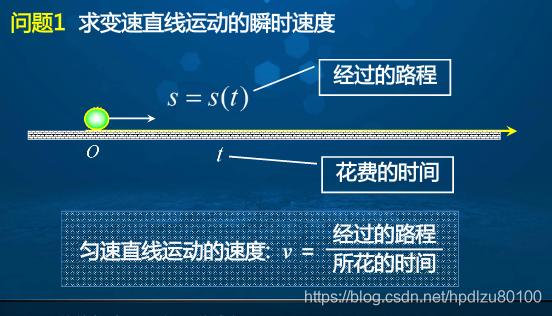
3. 问题求解1——求变速直线运动的瞬时速度

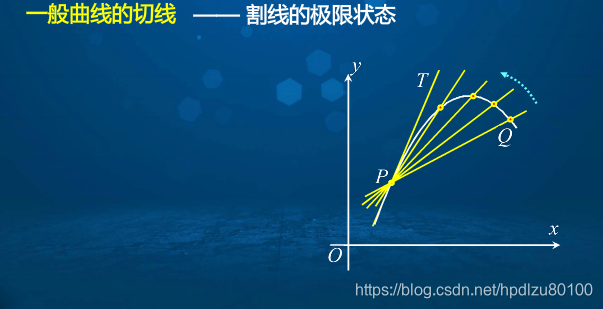
4. 问题求解2——求曲线的切线(问题1与2的共性:函数增量与自变量增量之比的极限)

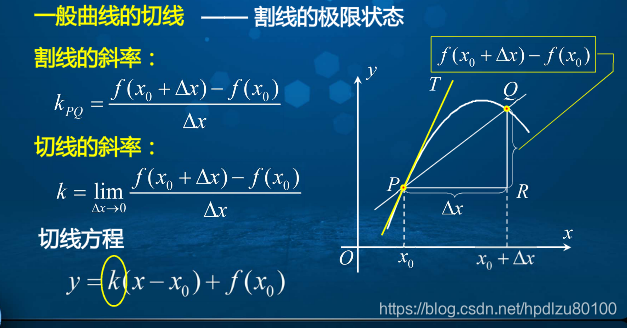
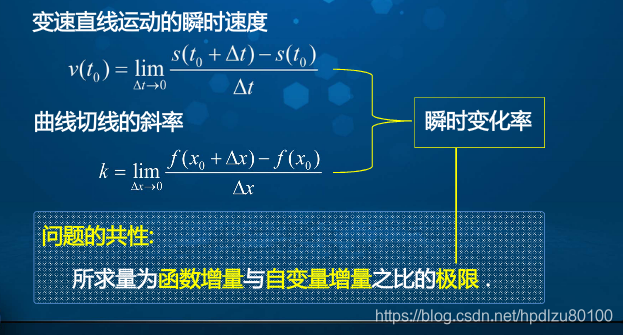
5. 导数的定义


7. 导数的几何意义

8. 函数在某处可导的充要条件是它在该处的左、右导数存在且相等

9. 可导必连续,连续不一定可导
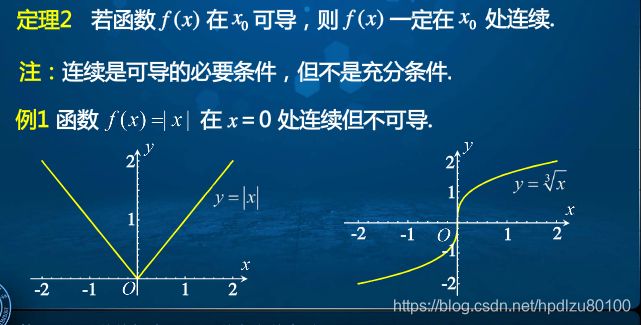
10. 可导在生活中的应用实例——儿童滑梯处处可导(曲线处处有明确的延伸方向)

11. 导函数(导数)的定义

12. 使用定义求导函数示例(常值函数、二次抛物线函数、反比例函数)
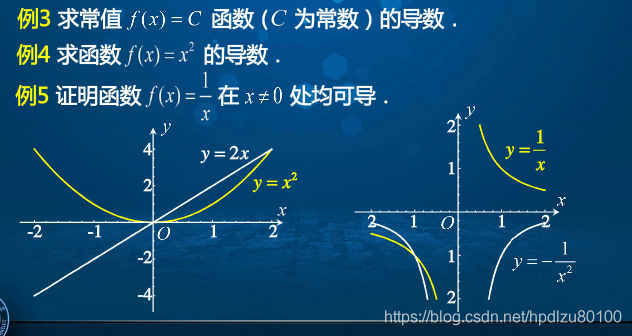










 本文深入探讨微积分中导数的概念,从微分学的产生背景到导数的定义及其几何意义,再到导数在生活中的应用实例,如儿童滑梯的处处可导性。文章还介绍了求导数的基本方法,并通过示例解析了常值函数、二次抛物线函数、反比例函数的导数计算。
本文深入探讨微积分中导数的概念,从微分学的产生背景到导数的定义及其几何意义,再到导数在生活中的应用实例,如儿童滑梯的处处可导性。文章还介绍了求导数的基本方法,并通过示例解析了常值函数、二次抛物线函数、反比例函数的导数计算。
















 4516
4516

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








