让微积分穿梭于工作与学习之间（7）：我自认为牛逼的成果之三：直接用定义求正切函数的导数

总的来说，求导数要比求原函数简单，这是因为导数是一个简单的极限表达式：

不论f(x)有多复杂，只要f(x)始终是初等数学函数，你又有足够耐性的话，那么代入进去总是能求得出来的，但是实际中没人会这么做。因为哪怕是最基本的初等数学函数，利用上式计算就已经很复杂了。再对他们进行复合或者四则运算的话，其计算过程就更繁琐了。所以一般教材的做法都是先把所有基本初等函数导数计算出来，再给出导数四则运算和复合的法则，然后就对给定函数进行分析分解，直至每一步都是基本初等函数之后，就代入基本初等函数导数公式中求得结果。

其中，有些基本初等函数也不会直接用定义来求，而是将其拆解为其它的基本初等函数再进行计算。例如已经运用定义算出了正余弦函数的导数：

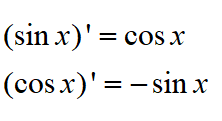
那么在求正切函数的导数时，就不再用定义了，而以除法的导数代之：

接着，除法导数的运算法则如下：

代入一下，即可得到

有了正余弦导数公式后，正切的求导过程可谓相当简单。

然后，正余弦函数的导数用定义来算也不难，这里就不给出了，教材一大把。原因在于弦函数在初等数学领域属于最简单的三角函数，两角和差公式比其它三角函数简单得多，然后还能轻松推导出更实用的积化和差以及和差化积公式。教材上给出的正弦导数计算过程，就是通过和差化积公式把分子部分变成一个项，然后就可以往下化简了。

但正切函数就没有所谓的和差化积公式了，其两角和差也比弦函数复杂得多：

正弦的两角和则不包含分母：

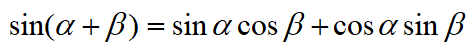
代入到导数定义的公式中，显然后者更容易处理。

但喜欢钻牛角尖的我，就非要把那个复杂的给代进去玩玩：

这种繁分数，看着真的很不舒服，但既然开始了，那就继续下去吧。先对分子中的分母进行通分。

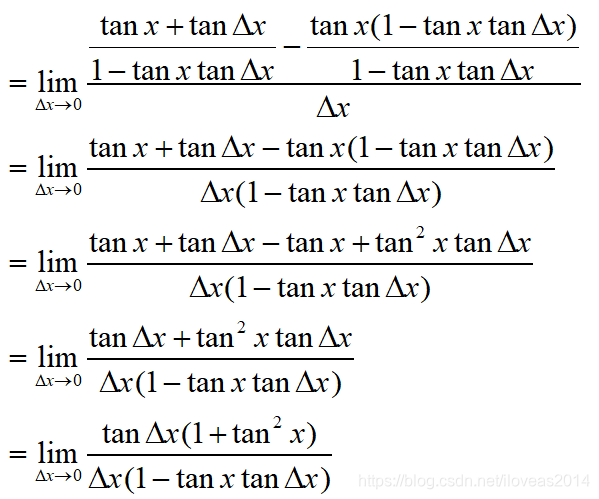
这下，我们可以把一些能代入Δx=0的项给代一下，分母里的1-tanxtan△x代入后得到1，可以代入，而△x=0则先不能代入。

1+tan²x跟△x无关，不用管了，可以直接提取出去。于是得到

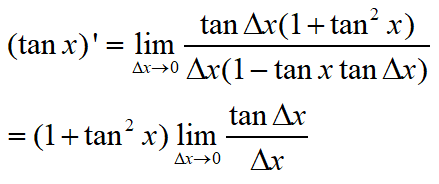
这里不得不提一个套路，就是基于夹逼定义的骚极限：

我们把正切分解为正弦和余弦，其中余弦函数在x趋于0的时候等于1，于是有

可见，结果跟用除法导数算出来的完全一样！

上篇我是说打算拿反正弦函数来展示的，但是我感觉反正弦太复杂了，大家可能一时半刻接受不来，所以我先拿了个相对简单的正切函数来进行过渡。由于两角和的正切仍然可以展开，且展开的结果只是因为有个稍复杂的分母而使得演算略繁琐。但只要有足够耐性，有一定的做题功底，那么用定义求正切函数导数还是比较轻松的。

而反三角函数就不是那么好伺候了。因为这个玩意儿，是没有公式可以给你展开或者跟其它的项进行合并。

那么，喜欢钻牛角尖的我最后是如何把这东西给拿下来的呢？且听下回分解！