测量校准原理

zhbi98

已于 2025-02-16 10:47:09 修改

阅读量795

点赞数 8

分类专栏：示波器技术文章标签：算法

于 2025-01-26 19:46:20 首次发布

转载文章的小伙伴请附上本文的链接，谢谢

本文链接：https://blog.csdn.net/jf_52001760/article/details/145371161

版权

示波器技术专栏收录该内容

3 篇文章

订阅专栏

测量校准原理

在实际测量中传感器实际测量值相比标准参考值（真实值）总是存在误差，即传感器无法准确的量化真实值，不仅如此，实际上两个相同的传感器在同一时刻测量同一个信号它们得出的结果也不同，为什么会这样？

请添加图片描述

这是因为传感器的物理特性受材料和制造工艺的限制，始终难以达到最优状态，同时也难以保证两个传感器的物理特性相同。

有没有可能让传感器在制造时达到理论物理特性，同时保证每个传感器物理特性相同，显然这是极为苛刻的，至少目前我们仅能无限地接近理论的极限，而无法直接突破理论，那是否就没有办法了呢？

1. 什么是校准

办法还是有的，除了改进制造工艺之外，我们可以通过在传感器内部对其测量到的数据进行矫正计算来补足实际测量与真实值的误差，即通过二次计算处理让测量值接近真实值，这就是校准。

请添加图片描述

值得一提的是，校准后也不能保证实际际测量值与真实值完全相同，校准只能 降低测量误差，保证实际测量值与真实值的误差最小。因为在实际中即使校准后的测量结果依旧会受到其工作环境的影响，例如温度，气压，工程就是这么的艰难，即使顶级标准设备也无法做到完全不存在误差，但标准设备距离理论确实是最近的。

下面我们一起了解一些校准方面的概念，并以万用表内部测量数据的校准为例，了解测量设备内部将实际测量值矫正至接近实际值的方法是什么，注意这种方法适用于各种测量设备矫正。

2. 不确定度

不确定度是指真值所在的数值范围。例如，如果电压表的测量不确定度为 ±0.1V，那么当测量显示的电压为 10.0V 时，真实电压值可能低至 9.9V 或高达 10.1V。如果 0.1V 不确定度的覆盖率为 95%，则 10V±0.1V 范围内包含真值的置信度就为 95%。幸运的是，大多数结果都倾向于集中在可能范围的中间部分，因为随机不确定性往往遵循高斯分布或呈正态钟形曲线。

注意，使用 “不确定度”（即可能的误差量）而不是 “准确度” 来描述测量设备的准确度。在测量行业，仪器制造商使用准确度指标来表示使用仪器时可能出现的预期误差范围。然而 VIM 提出了将 “不确定度” 作为首选术语来描述仪器的测量指标的指导方针，所以 “不确定度” 才是讨论误差量时正确的描述方式。

3. 误差关系

上面说了，虽然测量设备实际测量值相比标准参考值（真实值）总是存在误差，但是大多数结果都倾向于集中在可能范围的中间部分，因为随机不确定性往往遵循高斯分布（即分布关系呈正态钟形曲线）。

所以也就是说，虽然测量总是存在误差，但是误差会呈现一定的规律（即测量值和真实值之间会遵循某种关系），这种关系只有线性和非线性两种。

(1) 线性关系：指的是测量值和真实值之间的关系在特定的数值范围内保持一致，这种关系通常可以使用一次函数 $y = k x + b$ 来表示（其中 $y$ 为真实值 $x$ 为测量值）因此只要知道 $k$ 和 $b$ 就可以根据当前测量值 $x$ 得出真实值 $y$ ，测量值校准非常容易。

(2) 非线性关系：指的是测量值和真实值之间的关系在特定的数值范围内会发生改变，意味着两者的关系更复杂，不能使用一次函数 $y = k x + b$ 表示，需要使用更复杂的二次，三次函数关系式表示。还有一种办法是借助微分思想，将特定数值范围划分为更小的区间，测量值与真实值之间的关系在这更小的区间内来不及改变而保持一致，此时非线性关系就转化为了与之近似的多段线性关系，如下图。

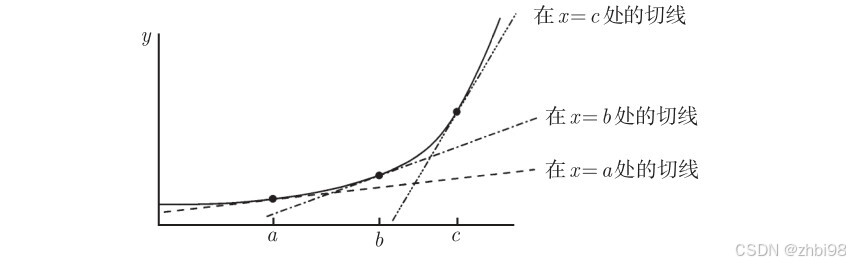
请添加图片描述

对于非线性的关系，重点是找出它们之间的复杂关系式是什么，这通常需要反复取样获得足够的测量样本才能推导。而多段线性则要划分出各个最优区间，并解出各区间线性关系式，所以测量值校准更困难。

(3) 随机关系：也叫不确定关系，测量值可以被校准的前提是它与真实值之间能呈现出某种简单或复杂规律（关系），否则任意变化的测量值无法被校准。

4. 线性校准

如果测量值和真实值的大小变化关系趋势在特定的范围内保持一致，那么说明测量值和真实值之间的关系是简单的，我们可以利用线性关系去校准测量值。

根据线性关系式 $y = k x + b$ 可以知道，最重要的一件事是如何求出 $k$ 和 $b$ ，其中 $k$ 表示测量值与真实值之间的倍数关系， $b$ 表示两者之间的偏移关系，如下图。

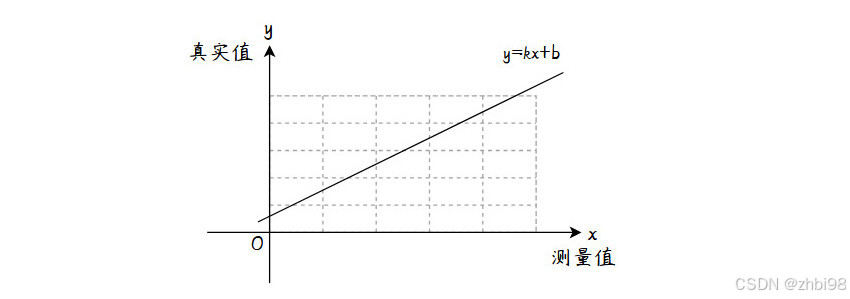
请添加图片描述

如果一次函数经过两点 $x_{0},y_{0})$ 和 $x_{1},y_{1})$ 根据一次函数性质可知：

$k=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}，b=y-kx$

其中 $b$ 可以取两点坐标 $x_{0},y_{0})$ 或 $x_{1},y_{1})$ 中的 $x, y$ 值来进行计算。

(1) 有了上面的分析之后，所以现在要做的是如何构造出两点坐标，根据上图（一次函数图像）可以知道 $x$ 轴对应的是测量值， $y$ 轴对应的是真实值，所以获取两个测量值和两个真实值即可构造两点。

(2) 构造两点时要在数值范围最小与最大处取对应测量值和真实值，线性关系式才能覆盖整个数值范围。在不输入信号时自然可以取得最小测量值，而对应的真实值则为 $0$ （是否为 0 视特性决定）。在输入最大信号时自然可以取得最大测量值，而对应的真实值则为输入的信号值。

什么是零偏？

如果测量设备不输入信号，直觉上来说测量设备取得的测量值应该为 0，但实际并不是这样，由于测量设备受到外部环境的干扰影响即使没有输入信号也可以取得微弱且随机变化的非零值，这就是零偏。

零偏虽然是随机变化的，但是可以取其平均值后，扣除零偏。很多测量设备要求断开输入信号连接执行自校正或自检操作就是为了获取零偏。

(3) 为了取得准确的最大测量值和真实值需要一台校准器，校准器可以输出值由你定义的纯净标准信号，该信号作为 “真实值” 输入待校准的测量设备，并且被程序获取用于参数计算。

请添加图片描述

(4) 现在就可以根据上面的分析，把一次函数斜率 $k$ 与截距 $b$ 的计算方法写成程序形式，如下：

/**
 * In fact, it only needs one observation and one training data 
 * to know the proportional relationship between observation and training.
 * _T_bias, _T_meas, Training dataset; Training Data.
 */
uint8_t _gain_Kp_bias(float bias, float meas, float _T_bias, 
    float _T_meas, float * Kp, float * b)
{
    float _Kp = 1.0f, _Kz = 0.0f;
    uint8_t ret = 0;

    if (meas != bias) _Kp = (_T_meas - _T_bias) / (meas - bias);

    if ((_Kp > 0.1f) && (_Kp < 10.0f)) {
        _Kz = _T_meas - (meas * _Kp);
        *Kp = _Kp;
        *b = _Kz;
        ret = 1;
    }

    /*info("Y_bias: %e _T_bias: %e Y_meas: %e _T_meas: %e _Kp: %f _Kz: %e", 
        Y_bias, _T_bias, Y_meas, _T_meas, _Kp, _Kz);*/

    return ret;
}

其中 bias 表示没有输入信号时最小信号测量值，_T_bias 表示没有输入信号时最小信号真实值，该值为 0。meas 表示输入最大信号时最大信号测量值，_T_meas 表示输入最大信号时最大信号真实值，该值就是校准器输出值。Kp 和 b 就是最终计算得到的一次函数需的 $k$ 与 $b$ 。

(5) 最后就可以根据实际测量值和计算得到的 Kp 和 b 以及 $y = k x + b$ 这个关系式来计算出实际测量值对应的真实值，因为比例因子 Kp 和固定误差消除因子 b 的存在，测量值一定可以被微调至真实值。

5. 非线性校准

借助微分思想可以用多段相连的线性线近似出非线性关系，就是把多段线性的直线连接在一起可以得到一幅折线图，只要确保每一段直线长度划分，倾斜角度足够的合理，那这个折线图就可以模拟出非线性的关键走势。

根据 “单点” 线性关系求解方法可知，求出线性关系式的关键是如何求出斜率 $k$ ，同样的多段线性也是这样，并且需要求出每一段的斜率 $k$ 。

现在以一个 “频率为参考补偿测量值” 的例子讲解非线性校准计算方法，在校准器输出交流电压时只改变频率不改变电压的情况下测量设备测到的电压信号与频率的关系图像如下图。

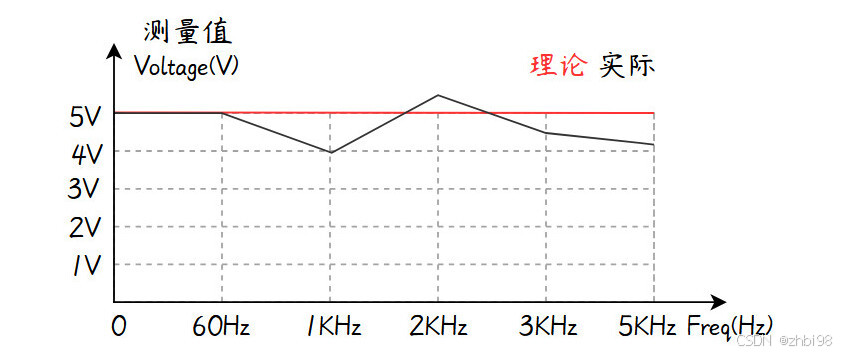
请添加图片描述

按照我们的直觉在电压不变的情况下无论如何改变频率电压测量值都因该保持不变，但是从上图可以看出实际上随着频率超过 60Hz 测量值就开始产生误差，并且测量值与频率变化建立的是图中黑色非线性函数关系。

5.1 线性段划分

与测量值建立非线性关系的是频率，所以借助微分的思想，将频率范围划分为更小的频率区间，把非线性的每个拐点（突变）位置作为区间分界点，意味着每个区间内不会再存在拐点。

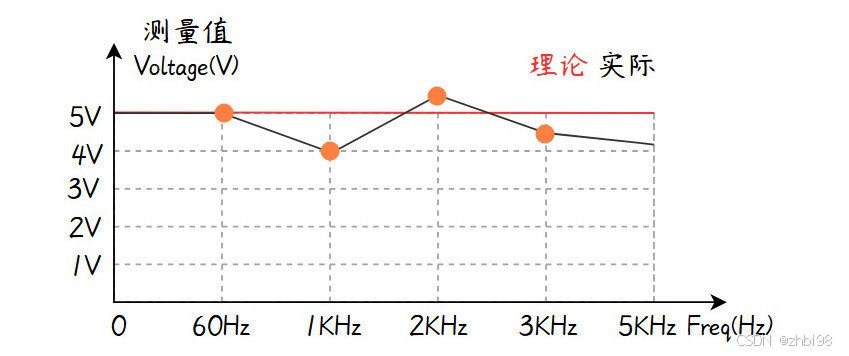
请添加图片描述

例如按照 (0, 60)，(60, 1k)，(1k, 2k)，(2k, 3k)，(3k, 5k) 划分后在每个频率区间内频率与测量值满足一次线性关系。

5.2 区间线性校准

线性区间划分完成后，指定一个区间（例如这里指定 (2k, 3k)）在该区间内可以使用一次函数 $y = k x + b$ 来表示这频率与测量值的线性关系，如下图（其中 $y$ 为测量值 $x$ 为频率值）在该区间内知道 $k$ 和 $b$ 就可以根据频率值 $x$ 得出测量值 $y$ 。

请添加图片描述

5.3 计算 K 值

在指定区间内，一次函数恰好经过区间边界的两点 $x_{0},y_{0})$ 和 $x_{1},y_{1})$ 根据一次函数性质可知：

$k=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}$

(1) 在实际测量中这两点是校准时获取的两个频率点和对应的测量值，调节好校准器输出值，然后把频率设置为该区间左边界频率值，记录下对应测量值，再把频率设置为该区间右边界频率值，记录下对应测量值（这两点也叫校准点）。

(2) 有了区间边界上的两点频率和测量值后就可以代入计算出 $k$ 值了，如下。

$k=\frac{V_{1}-V_{0}}{f_{1}-f_{0}}$

当 $f_{1}$ 为 3KHz 时 $V_{1}$ 为 4.5V， $f_{0}$ 为 2KHz 时 $V_{0}$ 为 5.5V，所以计算出 $k$ ，如下。

$k=\frac{4.5-5.5}{3000-2000}=-0.001$

注意 $k$ 值符号要取反，因为频率越大测量值越小，对应补偿输出增益应该越大。

(3) 上面的计算方法并没有问题，但是可以发现一个细节，即 $k$ 不是基于理想测量值计算出的斜率。既然在 60Hz 时测量值保持不变（例如 5V），可以考虑使用这一点作为基准来调整其他频率点的测量值，基于理想测量值可以得到两个比例。

$p_{0}=\frac{5}{5.5}, \ \ p_{1}=\frac{5}{4.5}$

写成通用表达式，即。

$p_{0}=\frac{V_{60Hz}}{V_{f0}}, \ \ p_{1}=\frac{V_{60Hz}}{V_{f1}}$

当频率从 60Hz 变化到 1KHz 过程中，测量值从离想 5V 向 4V 这个范围逐渐变化，但 2KHz 变化到 3KHz 过程中，测量值从 5.5V 向 4.5V 这个范围逐渐变化，所以要将测量值等比的变换回以理想 5V 为基准的变化。

(4) 现在从区间内取一个固定点，乘以这两个比例来重新定义区间边界上的两个理想测量值。这个固定点可以是区间内对应的实时测量值。

$V'_{0}=V_{real} \cdot p_{0}，V'_{1}=V_{real} \cdot p_{1}，$

有了上方的分析，总结出 $k$ 的计算表达式，如下。

$K=\frac{p_{0} \cdot V_{real}-p_{1} \cdot V_{real}}{f_{1}-f_{0}} \\ =\frac{\frac{V_{60Hz}}{V_{f1}}\cdot V_{real}-\frac{V_{60Hz}}{V_{f0}}\cdot V_{real}}{f_{1}-f_{0}}$