【自动驾驶】运动规划丨速度规划丨 T 型 / S 型速度曲线

正常的速度曲线算法有 T 型速度曲线控制、S 型速度曲线控制、正弦加减速控制的算法，每一种算法都各有特点。

1.T 型速度曲线

T 型速度曲线整个运动过程分为匀加速、匀速、匀减速三个阶段，在变速过程中，加速度 a 始终为设定的一个定值，给定若干个控制点，设定加速度为 a，加速度为 - a，匀速阶段速度为 vm(即整个运动最大速度)，以及总的运行时间 T，则速度、加速度、加加速度曲线如下图所示：

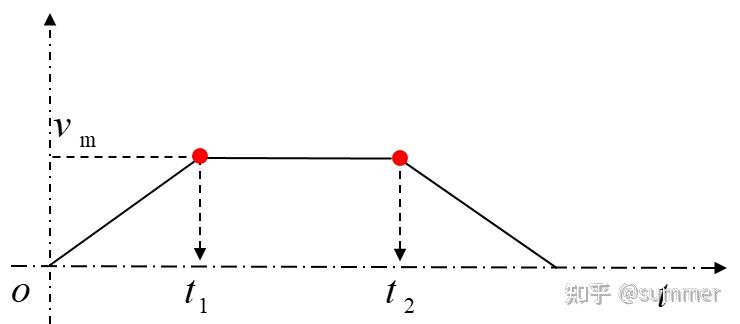
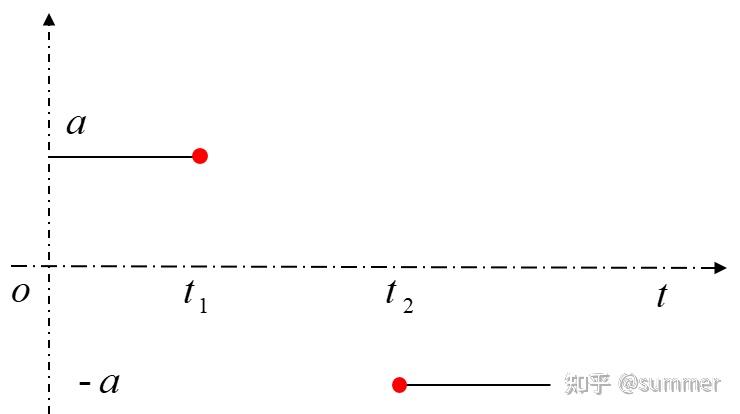
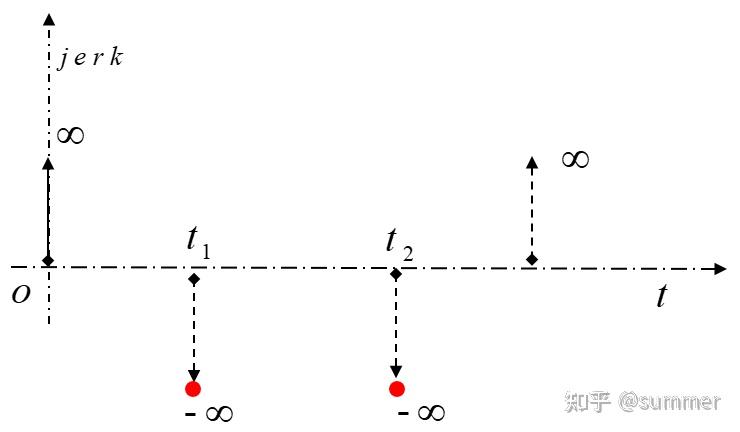
由图可知，T 型函数策略相对容易实现，但其加速度不连续，在加减速阶段与匀速阶段的衔接处，存在突变的情况，这会对车辆执行器造成冲击，影响驾乘舒适性。适用于紧急制动、矿区等对舒适性要求不高的场景。

2.S 型速度曲线

S 型速度曲线整个运动过程分为 7 个阶段，即加加速度阶段、匀加速阶段、减加速阶段、匀速段、加减速段、匀减速段、减减速段，不同阶段的速度衔接处加速度是连续的，且加速度的变化率可控，解决了 T 型速度曲线加速度存在的突变问题。S 速度曲线的速度、加速度和加加速度曲线如下所示：

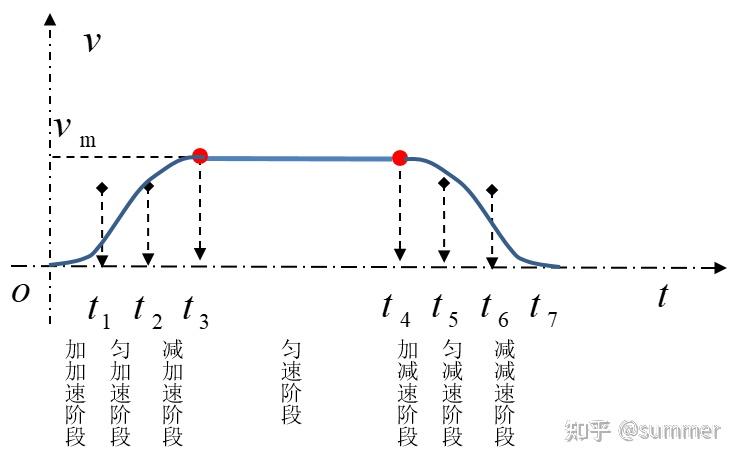
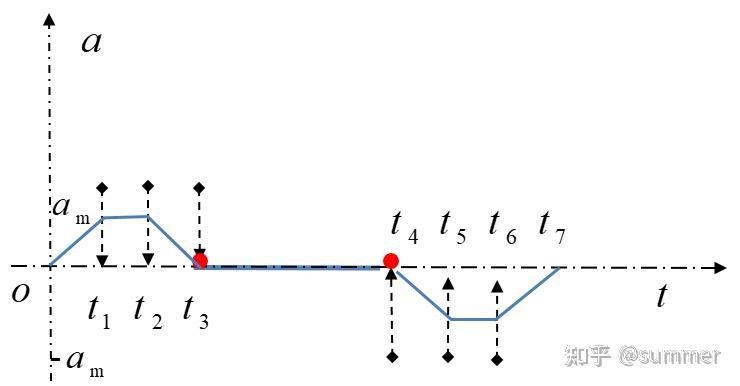
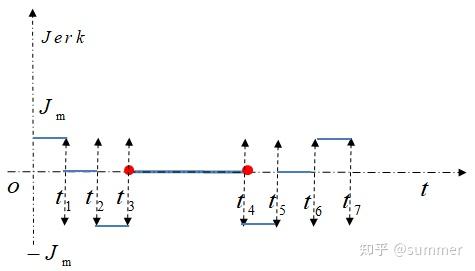
由图可知，S 型速度曲线柔性较好，解决了 T 型函数存在的加速度突变的问题，避免了车辆运动时候的柔性冲击，但由于分段较多、结构复杂，导致算法计算量较大，实现起来相对复杂。

3. 代码

---

"""
"""

import math
import numpy as np
import matplotlib.pyplot as plt


def T_speed(t, t1, t2, t3, v0, vm):
    a1 = (vm - v0) / t1
    a2 = -(vm - v0) / (t3 - t2)
    if (t >= 0 and t < t1):
        T_v = v0 + a1 * t
        T_a = a1
    elif (t >= t1 and t < t2):
        T_v = vm
        T_a = 0
    elif (t >= t2 and t < t3):
        T_v = a2 * (t - t3)
        T_a = a2
    else:
        T_v = 0
        T_a = 0

    return T_v, T_a


def S_speed(t, t1, t2, t3, a0, am):
    J1 = (am - a0) / t1
    J2 = -(am - a0) / (t3 - t2)
    if (t >= 0 and t < t1):
        S_a = a0 + J1 * t
        S_v = a0 * t + J1 * t ** 2 / 2

    elif (t >= t1 and t < t2):
        S_a = am
        S_v = am * t + (a0 - am) * t1 + J1 * t1 ** 2 / 2

    elif (t >= t2 and t < t3):
        S_a = J2 * (t - t3)
        S_v = J2 * t ** 2 / 2 - J2 * t3 * t + \
              (am * t2 + (a0 - am) * t1 + J1 * t1 ** 2 / 2 - J2 * t2 ** 2 / 2 + J2 * t3 * t2)
    else:
        S_a = 0
        t = t2
        vm = J2 * t ** 2 / 2 - J2 * t3 * t + (
                am * t2 + (a0 - am) * t1 + J1 * t1 ** 2 / 2 - J2 * t2 ** 2 / 2 + J2 * t3 * t2)
        S_v = vm
    return S_v, S_a


def main():


    for t in np.arange(0, 30, 1):
        plt.figure(1)
        [T_v,T_a] = T_speed(t, 10, 20, 30, 0, 10)

        ax1 = plt.subplot(2, 1, 1)
        ax2 = plt.subplot(2, 1, 2)
        plt.sca(ax1)
        plt.plot(t, T_v, 'or')  #
        plt.title(" speed" )
        plt.sca(ax2)
        plt.plot(t, T_a, 'og')  #
        plt.title(" acc")

        plt.figure(2)
        [S_v, S_a] = S_speed(t, 10, 20, 30, 0, 2)

        ax1 = plt.subplot(2, 1, 1)
        ax2 = plt.subplot(2, 1, 2)
        plt.sca(ax1)
        plt.plot(t, S_v, 'or')  #
        plt.title(" speed")
        plt.sca(ax2)
        plt.plot(t, S_a, 'og')  #
        plt.title(" acc")



    plt.axis("equal")
    plt.show()


if __name__ == '__main__':
    main()

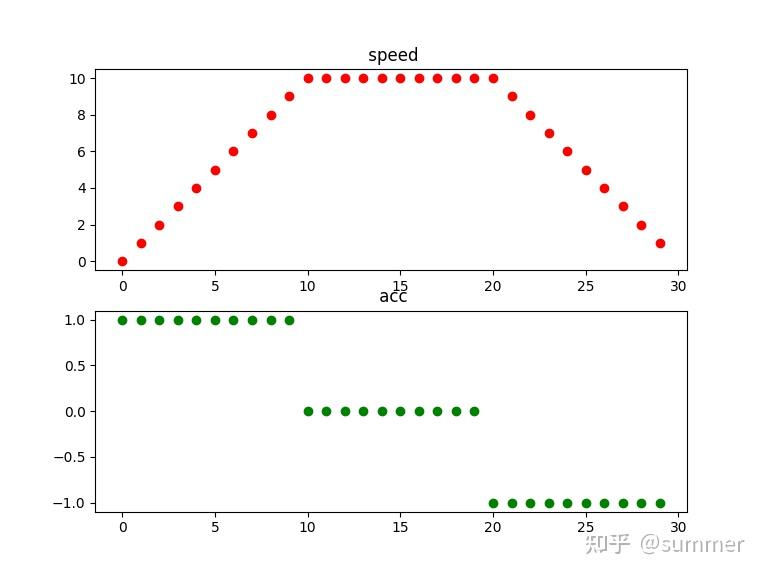
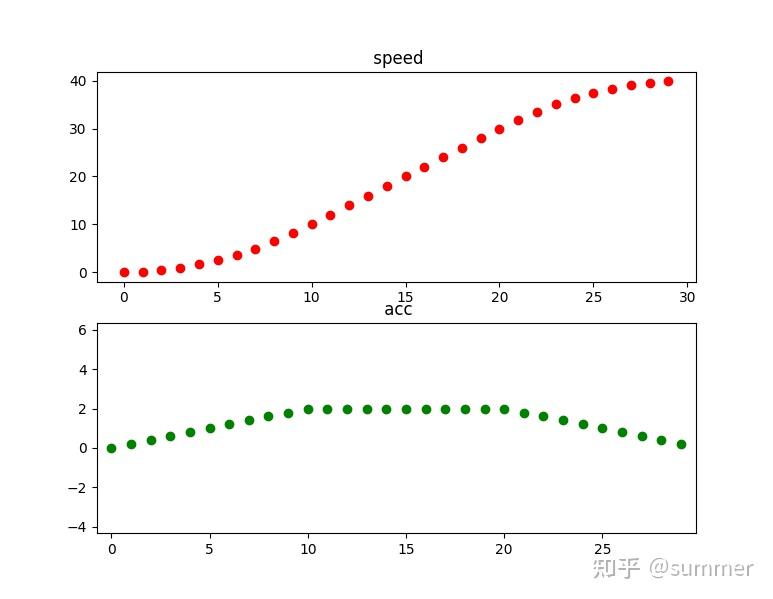T 型速度曲线 S 型速度曲线_魂淡林的博客 - CSDN 博客_s 型曲线一文教你快速搞懂速度曲线规划之 S 形曲线（超详细 + 图文 + 推导 + 附件代码）_GREYWALL-CSDN 博客_s 型速度曲线