Games101 03 - 变换

目录

1.Transformation 变换

1.1 意义

1.2 二维变换

1.2.1 Rotation（Reflection）旋转（反射）-正交矩阵

1.2.2 Scale 缩放-对角矩阵

1.2.3 Shear-剪切矩阵

1.2.4 Translate-齐次坐标系表示下的矩阵

1.2.5 Projection（降维）-秩小于行列数的方阵（秩可以理解为变换后空间的维数） / 非方阵...

1.3 Homogeneous Coordinates 齐次坐标

1.3.1 引入原因

1.3.2 Pot 与 Vector

1.3.3 Affine transformation 仿射变换

1.3.4 齐次坐标表示其他线性变换

1.4 Inverse Transform 逆变换

1.5 Order

---

1.Transformation 变换

1.1 意义

变换用来描述、实现运动

（线性）变换和矩阵两个词本质是一样的，前者强调过程，后者强调结果（变换后的基向量作为矩阵列向量）

1.2 二维变换

1.2.1 Rotation（Reflection）旋转（反射）-正交矩阵

因为不能改变长度，因此矩阵每一列每一行的平方和必须为1

AB≠BA，但是AB=B^T A^T，左乘变右乘只需要将两个矩阵交换顺序并分别进行转置操作即可

正交矩阵中关于哪个轴旋转，这个轴的基向量对应的列向量不变，另一列取负号

1.2.2 Scale 缩放-对角矩阵

1.2.3 Shear-剪切矩阵

1.2.4 Translate-齐次坐标系表示下的矩阵

1.2.5 Projection（降维）-秩小于行列数的方阵（秩可以理解为变换后空间的维数） / 非方阵...

1.3 Homogeneous Coordinates 齐次坐标

---

1.3.1 引入原因

1.可以用矩阵表示平移变换

无法将平移这种变换用一个矩阵表示，因为前面的部分的结果一定是X和Y前面乘一个系数。而根据表达式我们需要在X和Y后面恒加一个数，平移并不属于线性变换（原点改变了）而是仿射变换

我们总是greed，希望用一种方式表示所有情况，但这样一定会有代价，因此trade-off。就像算法，时间复杂度和空间复杂度往往是此消彼长的，引入的目的就是将所有的变换都可以用矩阵表示-消除平移带来的差异

有人可能会意识到这3维空间中的平移矩阵看起来好像4维空间的shear矩阵啊？其实完全正确在3维空间中的shear矩阵就可以视为二维空间中的平移矩阵

同理我们在四维空间中（4乘4矩阵）进行剪切，在三维空间中即为平移。这从几何上解释了为什么要到四维空间中去完成三维空间中的平移

线性变换有个最大的特点就是要过空间的原点，无论是多少维，而在3维空间中，要进行平移变换，其代表的目标空间，必然不经过原空间的原点，那么也这个平移变换就不是线性变换，正因于此，使用升维的方式，使三位空间的平移变换，转化为四维空间的线性变换，过四维原点，这也是为什么齐次坐标这种方式可以加入只表示线性变换的矩阵之中，因为n维仿射变换的特征满足n-1维线性变换的特征。

2.两条平行线会相交

在笛卡尔坐标系（欧几里得几何空间）中，两条平行线永远不会相交，但在投影空间中，如上图的两条铁轨却是会相交的，在无限远处会交于这一点，因为（∞，∞）在笛卡尔坐标系中是无意义的，因此笛卡尔坐标系中无法找到这个交点，但可以通过齐次坐标来解决这一个问题。

例如：笛卡尔坐标系下（1，2）的齐次坐标可以是（1，2，1），如果点（1，2）移动到无穷远处，在笛卡尔坐标下变为（∞，∞），此时齐次坐标为（1，2，0），因为（1/0，2/0）=（∞，∞），我们可以不用”∞“表示一个无穷远处的点

证明：两条直线可以相交

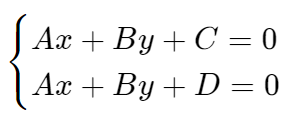
在笛卡尔坐标系中无解，因为C≠D，如果C=D两条直线就相同了

在透视空间中用齐次坐标x/w，y/w替代x、y，现在有一个解（x，y，0）即两条直线相交于无穷远处的该点

1.3.2 Pot 与 Vector

根据前面所阐述的”仿射变换在高维满足低维线性变换的特征“可知：将二维向量升维后的Z坐标设为0时，升维然后投影到xy平面缺少Z方向的维度信息因此表示的是向量，反之则是一个点。

点+向量的意思是一个点沿着向量的方向移动

一个点 + 一个点在齐次坐标的表示下意为2个点的中点，因为1+1=2，所以w=2，所以x和y都除以2即为中点

0是向量，1是（x，y，z）点，非1比如w表示（x/w，y/w，z/w）的点

1.3.3 Affine transformation 仿射变换

一个向量空间线性变换 + 平移。

仿射变换相比线性变换仍保持其3要素中的比例不变、变换前后都是直线，只少了原点保持不变这一条。

1.3.4 齐次坐标表示其他线性变换

先应用线性变换再平移

1.4 Inverse Transform 逆变换

逆变换从几何考虑很简单，就是如何执行上一步操作，撤销改变

1.5 Order

对向量从右向左的一个一个应用矩阵，顺序不同结果不同

利用结合律将多个矩阵结合为单个矩阵，等价于向量应用复合矩阵

可以把复杂的需求变换拆解为数个我们熟悉的变换

比如绕C旋转我们可以先将旋转C点移动到原点处然后绕原点旋转

——————————————————————————————————————————

Reference：

1.Games101课程

2.3B1B的线性代数课程

尾言：

还有许多很久以前记的笔记但不确定出处如有知道出处的朋友可以告诉我，仅供学习如有侵权我会及时删除

都看到这里啦，欢迎加群一起进一步交流游戏制作相关的技术哦！群：1005869797