games101-4-视图变换

Viewing transformation 视图变换

本篇笔记参考链接,写的真的很好!!!

简述:我们可以这样来描述视图变换的任务：将虚拟世界中以(x,y,z)为坐标的物体变换到 以一个个像素位置(x,y) 来表示的屏幕坐标系之中(2维)，这确实是一个较为复杂的过程，但是整个过程可以被细分为如下几个步骤：

(1)模型变换:modeling tranformation

这一步的目的是将虚拟世界中或者更具体点，游戏场景中的物体调整至他们应该在的位置

(2)摄像机变换:camera tranformation

在游戏中我们真正在乎的是摄像机(或者说眼睛)所看到的东西，也就是需要得到物体与摄像机的相对位置

(3)投影变换:projection tranformation

根据摄像机变换得到了所有可视范围内的物体对于摄像机的相对位置坐标(x,y,z)之后，便是根据是平行投影还是透视投影，将三维空间投影至标准二维平面([-1,1]^2)之上 （tips：这里的z并没有丢掉，为了之后的遮挡关系检测）

(4)视口变换:viewport transformation

将处于标准平面映射到屏幕分辨率范围之内，即[-1,1]^2→ \rightarrow→[0,width]*[0,height], 其中width和height指屏幕分辨率大小

例如:

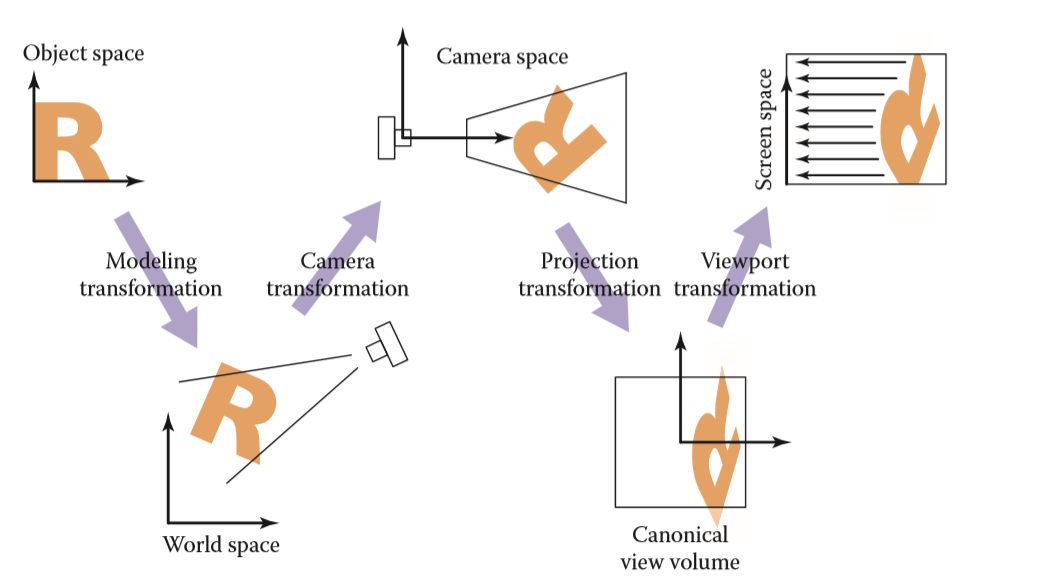
Modeling transformation 模型变换

就是上一节的内容:
利用基础的变换矩阵将世界当中的物体调整至我们想要的地方(旋转，平移，缩放)

Camera tranformation 摄像机变换

摄像机变换的目的是 得到所有可视物体与摄像机的相对位置

又因为,相机和物体在相对位置的情况下,是相对静止的,因此,可以把物体和摄像机一起做移动，如果能够把摄像机的坐标轴(假设为u,v,w 分别对应原世界空间中的x,y,z)移动到标准的x，y，z轴，那么此时物体的坐标自然便是相对坐标了

因此核心问题就 变成了如何表示或者说如何将camera的坐标系与原世界坐标系重合

首先,定义三个东西:

(1) eye postion : 相机或眼睛位置 为 $e$
(2) gaze postion : 观察方向 为 $\vec{g}$
(3) view-up vector : 视点正上方向 为 $\vec{t}$ //假设相机的朝向是正着的,也就是不是倾斜的拍摄

我们是想让相机的位置在原点,然后,观察方向为-z方向,视点正上方为y方向,也就是这样:

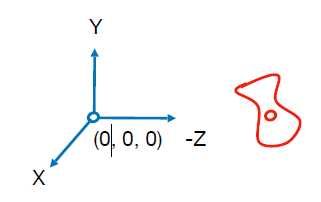
也就是要做这样一个事情:

Transform the camera by $M_{view}$:So it’s located at the origin, up at Y, look at -Z

如图所示:

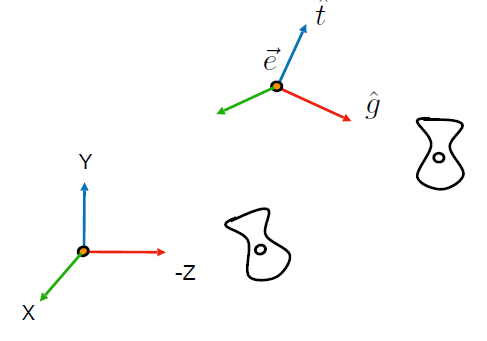
因此该矩阵需要实现三个效果:

1. 将相机平移至原点

   $$T_{\text{view }}=\left[\begin{array}{cccc}1& 0& 0& -x_e\\ 0& 1& 0& -y_e\\ 0& 0& 1& -z_e\\ 0& 0& 0& 1\end{array}\right]$$

2. 通过旋转矩阵将g转至-z方向上

3. 通过旋转矩阵将t转至y方向上 //然后通过g×t就可以得到x

   这一点如果正向去想的话可能会比较难,但是我们可以反向想,也就是我们想要g到-z方向上去,可以先求出把-z转到g上面去,然后求出旋转矩阵,再将此矩阵求逆(由于旋转矩阵是正交矩阵,所以求逆也就是求转置),就是将g转到-z上的旋转矩阵了

   所以,很简单可以求出,将z转到g上去的旋转矩阵为:
   $$R_{\text{view }}^{-1}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& x_t& x_{-g}& 0\\ y_{\hat{g}\times \hat{t}}& y_t& y_{-g}& 0\\ z_{\hat{g}\times \hat{t}}& z_t& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]$$

   而它的逆矩阵就是:

   $$R_{\text{view }}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& y_{\hat{g}\times \hat{t}}& z_{\hat{g}\times \hat{t}}& 0\\ x_t& y_t& z_t& 0\\ x_{-g}& y_{-g}& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]$$

从而可以得出,最终的过程为:

$$M_{\text{view }}=R_{\text{view }}{T}_{\text{view }}$$
$$M_{\text{view }}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& y_{\hat{g}\times \hat{t}}& z_{\hat{g}\times \hat{t}}& 0\\ x_t& y_t& z_t& 0\\ x_{-g}& y_{-g}& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& -x_e\\ 0& 1& 0& -y_e\\ 0& 0& 1& -z_e\\ 0& 0& 0& 1\end{array}\right]$$

注:所有矩阵都是左乘,最右边的矩阵代表第一步操作移至原点，旁边那个矩阵则代表第二三步操作将坐标系重合

Projection tranformation 投影变换

投影变换主要处理将三维中的物体压缩为二维

Orthographic projection 正交投影

• 正交投影举例:

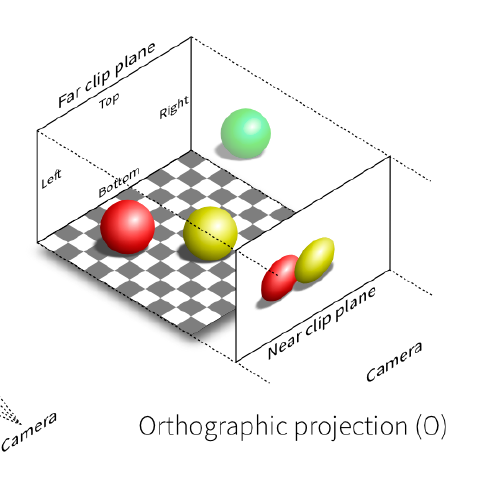
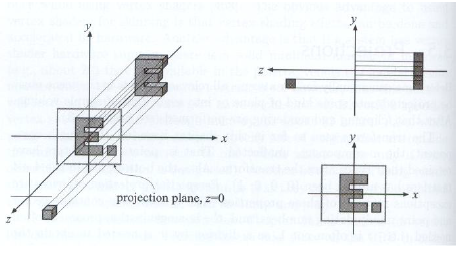
在正交投影中，坐标的相对位置都不会改变，所有光线都是平行传播，我们只需将物体（可视部分）全部转换到一个$[-1,1{]}^3$ 的空间之中即可（其中x，y坐标便是投影结果，保留z是为了之后的遮挡检测）

注:为什么要压缩到一个小立方体呢？

其实这只是为了之后的计算更加的方便而已
在转换到屏幕坐标的时候就会重新拉伸回来,不必太做纠结
只需抓住正交投影的变化核心是:所有物体的相对大小位置都不会有任何变化。

• 如何进行正交投影:
  1. 首先图形的中心移至原点
  2. 将大小缩小到-1~1之间
     总结一句话:Translate (center to origin) first, then scale (length/width/height to 2)
  

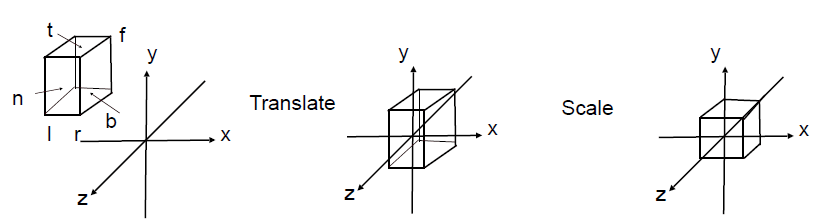
写出转换矩阵为(仍然是从右往左乘):
$$M_{\text{ortho }}=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& -\frac{r+l}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\end{array}\right]$$

Perspective projection 透视投影

• 透视投影举例:

  
  

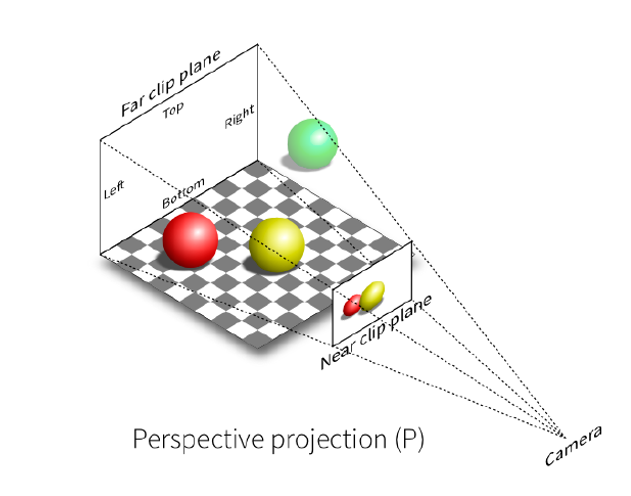
透视投影遵循一个法则,那就是 近大远小

• 如何转换

思路就是,如下图,先将后面的f平面压缩至和前面的n平面一样的大小,然后再利用正交投影进行转化

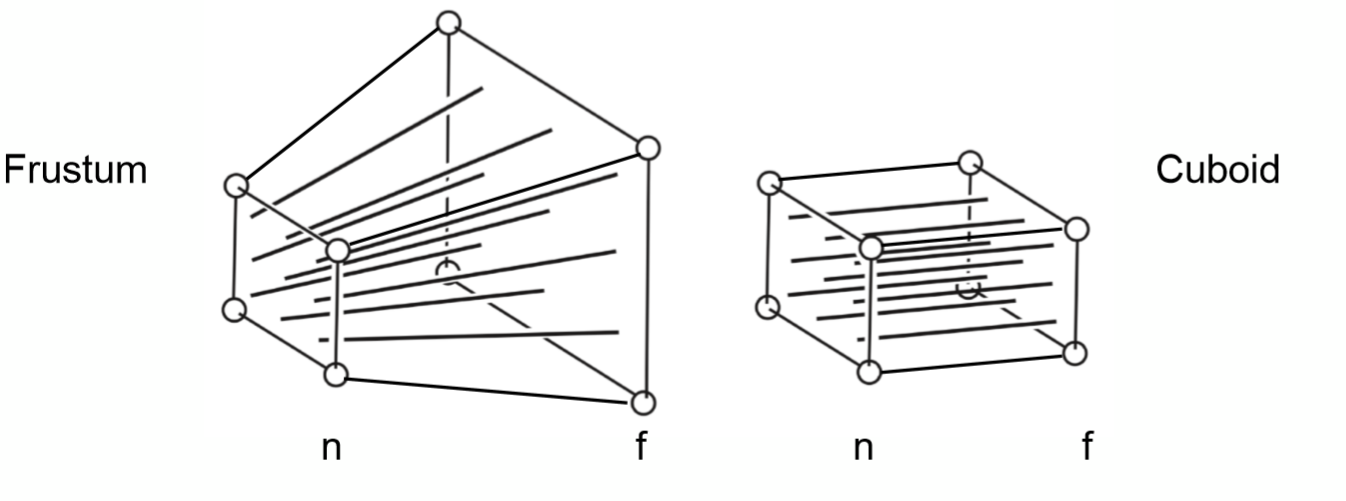
首先,我们先假定n整个平面所处的位置不变,f平面所处的位置也是不变的,那么分别从侧面和上面看去,可以看到下图所示的内容

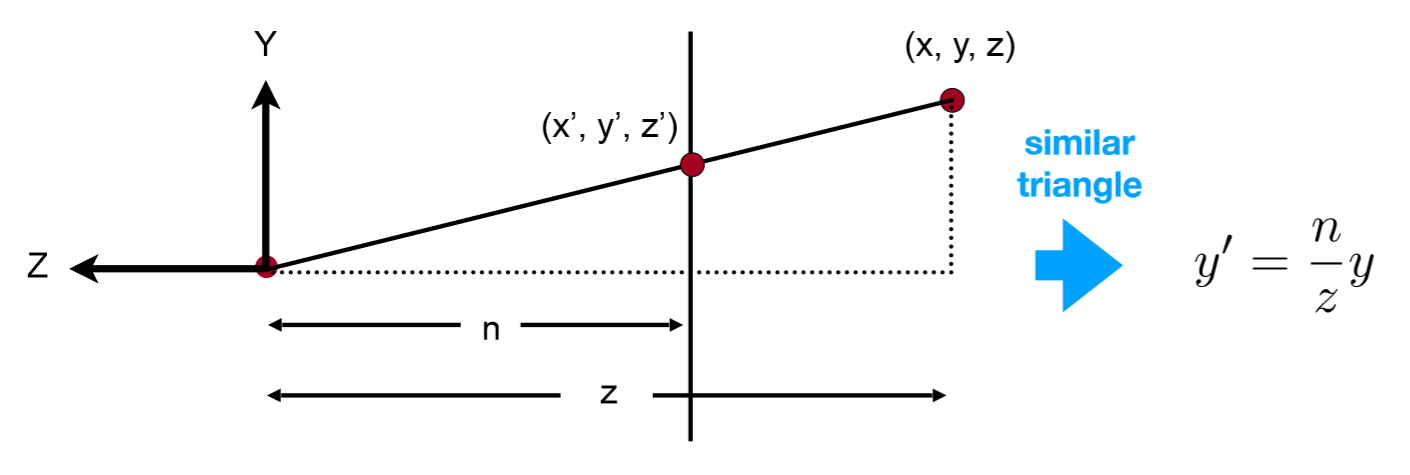
由相似三角形就很容易的到压缩至一样后的坐标,可以得到 $y与y^{{}^{\prime }}$ 的对应关系,同理,从上往下看也是一样的,可以得到 $x与x^{{}^{\prime }}$的对应关系

$$y^{\prime }=\frac{n}{z}y{x}^{\prime }=\frac{n}{z}x$$

$$\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)\Rightarrow \left(\begin{array}{c}nx/z\\ ny/z\\ \text{ unknown }\\ 1\end{array}\right)==\left(\begin{array}{c}nx\\ ny\\ \text{ still unknown }\\ z\end{array}\right)$$

那么,如何从第一个矩阵变换到第二个矩阵:这个就是我们要求的变换矩阵:该矩阵可以实现:
$$M_{\text{persp }\to \text{ ortho }}^{(4\times 4)}\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left(\begin{array}{c}nx\\ ny\\ \text{ unknown }\\ z\end{array}\right)$$

（如果形象化的描述一下的话，就是利用这个变换矩阵将整个空间压缩了一下，使其对应了真正透视投影的坐标，最后不要忘了要利用正交转换）

首先，这个矩阵的前两行和最后一行是能很快确定出来的，根据最后的齐次坐标，也就是:
$$M_{\text{persp }\to \text{ ortho }}=\left(\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ ?& ?& ?& ?\\ 0& 0& 1& 0\end{array}\right)$$
那么如何确定第三行呢，这里就要运用透视投影的一个性质：
可视空间，即本节第一张图的Frustum的前后面变换之后z坐标不变

设第三行为(0,0,A,B) ,利用这个性质分别代入远近平面的任意两点就可以列出两个等式

$$\left(\begin{array}{llll}0& 0& A& B\end{array}\right)\left(\begin{array}{l}x\\ y\\ n\\ 1\end{array}\right)=n^2$$

同理,f也是不会改变的,也有这个等式:

$$\left(\begin{array}{llll}0& 0& A& B\end{array}\right)\left(\begin{array}{l}x\\ y\\ f\\ 1\end{array}\right)=n^2$$

$$\begin{array}{ll}An+B=n^2& A=n+f\\ Af+B=f^2& B=-nf\end{array}$$

最后的一步，将这个被压缩过的空间，重新正交投影成标准小立方体，故定义透视投影变换$M_{per}$为:
$$M_{per}=M_{\text{ortho }}{M}_{\text{persp }\to \text{ ortho }}$$
同样是从右往左去乘,最终结果为:
$${\mathbf{M}}_{\text{per }}=\left[\begin{array}{cccc}\frac{2n}{r-l}& 0& \frac{l+r}{l-r}& 0\\ 0& \frac{2n}{t-b}& \frac{b+t}{b-t}& 0\\ 0& 0& \frac{f+n}{n-f}& \frac{2fn}{f-n}\\ 0& 0& 1& 0\end{array}\right]$$

Viewport transformation视口变换

这一步就很简单了，就是两个范围空间的转换 $[-1,1{]}^2\to [0,width]\ast [0,height]$ ,这里直接套公式即可

$$M_{\text{viewport }}=\left(\begin{array}{cccc}\frac{\text{ width }}{2}& 0& 0& \frac{\text{ width }}{2}\\ 0& \frac{\text{ height }}{2}& 0& \frac{\text{ height }}{2}\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$$

至此历经上述4个变换，我们就已经成功的把游戏世界的任意可视物体转换到屏幕上了！

$$\text{ 总结：变换 }M=M_{\text{view }}{M}_{\text{per }}{M}_{\text{cam }}{M}_{\text{model }}$$