NESTEROV ACCELERATED GRADIENT AND SCALE INVARIANCE FOR ADVERSARIAL ATTACKS论文解读

摘要

在黑盒设定下，大多数现有的攻击方式转移性较差。在这篇文章中，从将对抗样本的生成看作一个优化过程的角度出发，我们提出两种新的生成对抗样本的方式，称为Nesterov Iterative Fast Gradient Sign Method (NI-FGSM) 以及 Scale-Invariant attack Method (SIM)。NI-FGSM旨在将Nesterov accelerated gradient加入到迭代攻击中，从而有效提高对抗样本的转移性。SIM基于我们对深度学习模型尺度不变性的发现，为此，我们优化不同尺度的对抗扰动来避免过拟合。NI-FGSM和SIM可以集成在一起来构建基于梯度的鲁棒攻击，从而针对防御模型生成转移性更好的对抗样本。实验结果显示我们的攻击方法比SOTA 基于梯度的攻击方法具有更高的可转移性和更高的攻击成功率。

介绍

在本文中，我们将对抗样本的生成过程视为一个优化过程，，并提出了两种提高对抗样本转移性的新方法： Nesterov Iterative Fast Gradient Sign Method (NI-FGSM) and Scale-Invariant attack Method (SIM)。

• 受到Nesterov accelerated gradient在传统优化方面优于momentum的启发，我们将Nesterov accelerated gradient 应用到基于梯度的迭代攻击中。我们期望 NI-FGSM could replace the momentum iterative gradient-based method (Dong et al., 2018) in the gradient accumulating portion并且有更高的性能。
• 此外，我们发现深度学习具有尺度不变性，并提出了Scale-Invariant attack Method (SIM)，通过优化输入图像不同尺度副本上的对抗扰动来提高对抗样本的转移性。SIM可以避免白盒模型被攻击时“过拟合”，并生成针对其他黑盒模型时转移性更好的对抗样本。
• 我们发现将我们的NI-FGSM以及SIM和现有的基于模型的攻击方法组合起来能提高对抗样本的攻击成功率

在ImageNet数据集上的大量实验表明，我们的方法攻击正常训练的模型和对抗训练的模型时攻击成功率均高于现有的baseline。我们最好的攻击方法是SI-NI-TI-DIM（Scale-Invariant Nesterov Iterative FGSM integrated with translation-invariant diverse input method），在黑盒设定下，针对对抗训练模型的平均成功率为93.5%。为了进一步证明，我们通过攻击最新的鲁棒防御方法来评估我们的方法。结果表明，我们的攻击方法可以生成比基于梯度的SOTA攻击具有更高可转移性的对抗样本。

2 前置介绍

2.1 notation

2.2 攻击方法

现在已经存在许多方法来生成对抗样本。我们进行简短介绍：

Fast Gradient Sign Method（FGSM）： FGSM通过单步更新最大化loss function $J(x^{adv},y^{true})$来生成对抗样本$x^{adv}$：

$$x^{adv}=x+ϵ\cdot \text{sign}({\nabla }_{x}J(x,y^{true}))$$

这里$\text{sign}(\cdot )$ restricts the perturbation in the $L_{\infty }$ norm bound。

Iterative Fast Gradient Sign Method（I-FGSM）： 通过在FGSM的基础上添加一个较小的步长$\alpha$我们可以得到FGSM的迭代版本：

x 0 = x , x t + 1 a d v = C l i p x ϵ { x t a d v + α ⋅ sign ( ∇ x J ( x t a d v , y t r u e ) ) } x_0=x,\quad x_{t+1}^{adv}=Clip_x^{\epsilon}\{x_{t}^{adv}+\alpha\cdot\text{sign}(\nabla_xJ(x_t^{adv},y^{true}))\} x0​=x,xt+1adv​=Clipxϵ​{xtadv​+α⋅sign(∇x​J(xtadv​,ytrue))}

这里$Cli{p}_x^{ϵ}(\cdot )$函数restricts generated adversarial examples to be within the $ϵ$-ball of x.

Projected Gradient Descent (PGD)： PGD攻击是一种较强的FGSM的迭代变体。It consists of a random start within the allowed norm ball and then follows by running several iterations of I-FGSM to generate adversarial examples.

待补充 3

3 方法

3.1 动机

和训练神经网络的过程类似，生成对抗样本的过程可以被看作优化问题。在优化阶段，被攻击的白盒模型可以被是为训练过程中的训练数据。对抗样本可以看成待优化的参数。然后在测试阶段，用于评估对抗样本的黑盒模型可以被视为测试数据。

从优化的视角来看，对抗样本的转移性和训练后模型的泛化性类似。因此，我们可以将用于提升模型迁移性的方法迁移到生成对抗样本的过程中，通过这样来提升对抗样本的转移性。

现在已经提出了许多方法来提升深度学习模型的泛化性，我们可以将他们分为两类：

1. 更好的优化算法，例如Adam优化器
2. 数据扩充

相对应地，用于提升对抗样本转移性的方法同样可以被分为两类：

1. 更好的优化算法：例如MI-FGSM，应用了momentum的思想
2. 模型扩充（例如在多个模型上的ensemble攻击）

基于上述分析，我们旨在通过应用Nesterov accelerated gradient的思想进行优化并且使用一组缩放过的的图片来实验模型扩充，进而提升对抗样本的可转移性。

3.2 Nesterov Iterative Fast Gradient Sign Method

Nesterov Accelerated Gradient (NAG) (Nesterov, 1983)是普通梯度下降方法的一个变体，可以加速训练过程并显著提升收敛性。NAG可以被看作是改进的momentum方法，其公式表示如下：

$$\begin{gathered} v_{t+1}=\mu \cdot v_t+{\nabla }_{{\theta }_t}J({\theta }_t-\alpha \cdot \mu \cdot v_t) \\ {\theta }_{t+1}={\theta }_t-\alpha \cdot v_{t+1} \end{gathered}$$

典型的基于梯度的迭代攻击（例如，I-FGSM）greedily perturb the images in the direction of the sign of the gradient at each iteration，这会导致陷入较差的局部最优解，并且相比单步攻击（例如FGSM）而言转移性较差。Dong et al. (2018) 表明在攻击时使用momentum (Polyak, 1964) 可以稳定更新方向，这有助于摆脱较差的局部最优值并提高可转移性。和momentum相比，除了稳定更新方向外，NAG的anticipatory update为之前累计的梯度提供了一个修正，helps to effectively look ahead. NAG的这种looking ahead性质能帮助我们更容易且更快地逃离较差的局部最优解，从而改善可转移性。

我们将NAG集成到迭代梯度攻击中来利用NAG的looking ahead性质从而构建更鲁棒的对抗攻击，我们将其称为NI-FGSM（Nesterov Iterative Fast Gradient Sign Method）。特别地，we make a jump in the direction of previous accumulated gradients before computing the gradients in each iteration. 以$g_0=0$为开始，NI-FGSM的更新过程可以公式化如下：

x t n e s = x t a d v + α ⋅ μ ⋅ g t g t + 1 = μ ⋅ g t + ∇ x J ( x t n e s , y t r u e ) ∥ ∇ x J ( x t n e s , y t r u e ) ∥ 1 x t + 1 a d v = Clip x ϵ { x t a d v + α ⋅ sign ( g t + 1 ) } x_t^{nes}=x_t^{adv}+\alpha\cdot\mu\cdot g_t\\ g_{t+1}=\mu\cdot g_t+\frac{\nabla_xJ(x_t^{nes},y^{true})}{\Vert\nabla_xJ(x_t^{nes},y^{true})\Vert_1}\\ x_{t+1}^{adv}=\text{Clip}_x^{\epsilon}\{x_t^{adv}+\alpha\cdot\text{sign}(g_{t+1})\} xtnes​=xtadv​+α⋅μ⋅gt​gt+1​=μ⋅gt​+∥∇x​J(xtnes​,ytrue)∥1​∇x​J(xtnes​,ytrue)​xt+1adv​=Clipxϵ​{xtadv​+α⋅sign(gt+1​)}

这里$g_t$表示在迭代到第$t$轮后积累的梯度，$\mu$指代$g_t$的decay factor。

3.3 Scale-Invariant Attack Method

除了使用更好的优化算法外，我们同样可以通过模型扩充来提高对抗样本的可转移性。首先我们通过如下方式对模型扩充和loss-preserving转换进行一个正式定义：

定义1 Loss-preserving转换： 给定一个输入$x$，它的真值标签 $y^{true}$ 以及一个分类器 $f(x):x\in \mathcal{X}\to y\in \mathcal{Y}$（损失函数使用交叉熵损失 $J(x,y)$）。如果存在一个输入转换$\mathcal{T}(\cdot )$满足对任意的输入$x\in \mathcal{X}$，$J(\mathcal{T}(x),y^{true})\approx J(x,y^{true})$，那么我们称$\mathcal{T}(\cdot )$是一个loss-preserving转换。

定义2 Model Augmentation： 给定真值标签为 $y^{true}$ 的输入 $x$ 以及一个使用交叉熵 $J(x,y)$ 作为损失函数的模型$f(x):x\in \mathcal{X}\to y\in \mathcal{Y}$，如果存在一个loss-preserving转换 $\mathcal{T}(\cdot )$，那么我们可以从原始模型 $f$ 衍生得到一个新的模型 $f^{\prime }(x)=f(\mathcal{T}(x))$。我们将这样的衍生过程称为模型扩充。

直观地讲，与通过提供更多的训练数据来提高模型的泛化性类似，通过同时攻击多个模型也可以提高对抗样本的可转移性。Dong et al. (2018) 通过攻击一组模型来增强基于梯度的攻击。然而，这种方法需要训练一组不同的模型进行攻击，计算成本过大。相反，在这篇文章中，我们通过模型扩充来从原始模型中导出一组模型，这是通过loss-preserving转换来获得多个模型的一种简单方法。

为了得到loss-preserving转换，我们发现深度神经网络除了平移不变性外还可能有尺度不变性。具体而言，对于同一模型上的原始图像和缩放图像的损失值是类似的，这在4.2节中得到了实验验证。因此，尺度变换可以作为一种模型扩充方法。在上述分析的推动下，我们提出了一种Scale-Invariant attack Method (SIM)，该方法优化输入图像在不同尺度副本上的对抗扰动：

$$\begin{gathered} \underset{x^{adv}}{\mathrm{argmax}}\frac{1}{m}\sum _{i=0}^{m}J(S_i(x^{adv}),y^{true}) \\ s.t.\Vert x^{adv}-x{\Vert }_{\infty }\le ϵ \end{gathered}$$

这里$S_i(x)=x/2^i$表示尺度因子为$1/2^i$时输入图片$x$的尺度副本，$m$ 表示尺度副本的数量。使用SIM可以让我们在不训练多个模型的情况下通过模型扩充成功实现ensemble攻击。更重要的是，这可以避免在白盒模型上的过拟合并且生成转移性更好的对抗样本。

3.4 攻击算法

在生成对抗样本的梯度处理过程中，NI-FGSM算法引入了一种更好的优化算法来在每步的迭代中稳定更新方向。对于生成对抗样本的ensemble攻击，SIM引入了模型扩充来从单个模型中获取多个模型进行攻击。因此，NI-FGSM以及SIM可以很自然地结合在一起从而构建更强的攻击，我们将其称为SI-NI-FGSM（Scale-Invariant Nesterov Iterative Fast Gradient Sign Method）。这个算法在Algorithm 1中进行了总结。

In addition, SI-NI-FGSM can be integrated with DIM (Diverse Input Method), TIM (TranslationInvariant Method) and TI-DIM (Translation-Invariant with Diverse Input Method) as SI-NI-DIM, SINI-TIM and SI-NI-TI-DIM, respectively, to further boost the transferability of adversarial examples. The detailed algorithms for these attack methods are provided in Appendix A.

4 实验结果

在这一节，我们提供了我们所提出的方法效果更好的实验证据。我们首先给定实验设定，然后提供了对于深度学习模型尺度不变性的探索。然后，我们将所提出的方法与第4.3节和第4.4节中的baseline方法在正常训练模型和对抗训练模型上的结果进行比较。除了基于对抗训练的防御模型之外，我们还在第4.5节中量化了所提出方法对其他高级防御的有效性。关于NI-FGSM和MI-FGSM之间的比较以及与经典攻击的比较的其他讨论，请参见第4.6节。

4.1 实验设定

数据集： 我们从ILSVRC 2012验证集中随机选择了1000张属于1000个类别的图像，这些图像几乎被所有测试模型正确分类。

模型： 对于正常训练的模型，我们考虑Inception-V3（Inc -V3），Inception-V4（Cin -V4），Inception-Resnet-V2（IncRes-V2）和RESNET-V2-101（RES-101）。对于对抗训练的模型，我们考虑${\text{Inc-v3}}_{ens3}$、${\text{Inc-v3}}_{ens4}$和${\text{IncRes-v2}}_{ens}$。

此外，我们还引入了其他高级防御模型：high-level representation guided denoise（HGD）、random resizing and padding（R&P）、NIPS-r31、feature distillation（FD），purifying perturbation via image compression model（Comdefend）和randomized smoothing（RS）。

Baselines： 我们将我们的方法与DIM（Xie et al.，2019）、TIM和TI-DIM相结合，以展示SI-NI-FGSM在这些baseline上的性能改进。我们将我们的SI-NI-FGSM与其他攻击分别集成为SI-NI-DIM、SI-NI-TIM和SI-NI-TIM-DIM。

Hyper-parameters： 对于超参数，我们遵循（Dong等人，2018）中的设置，最大扰动为 $ϵ=16$，迭代次数 $T=10$，步长 $\alpha =1.6$。对于MI-FGSM，我们采用默认的衰减因子 $\mu =1.0$。对于DIM，transformation probability设置为0.5。对于TIM，我们采用高斯核，核的大小设置为$7\times 7$。对于我们的SI-NI-FGSM，尺度副本的数量设置为$m=5$。

4.2 尺度不变性特征

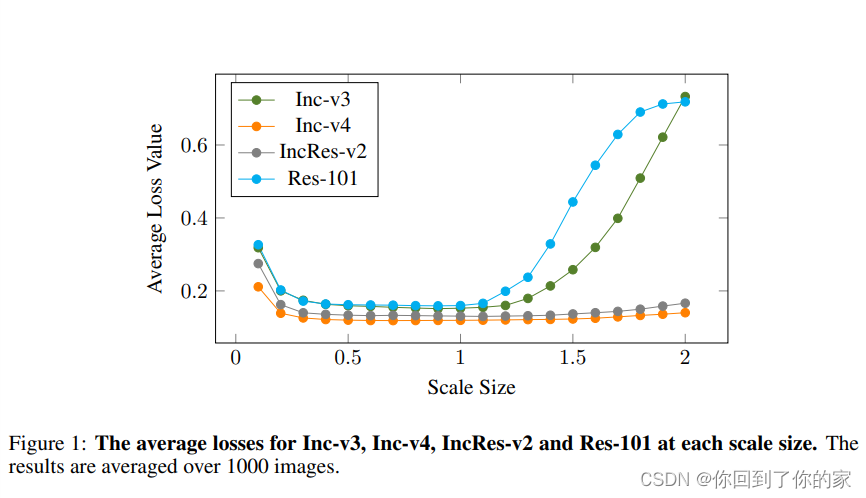
为了验证深度神经网络的尺度不变性，我们从ImageNet数据集中随机选择1000幅原始图像，并将尺度大小保持在[0.1,2.0]范围内，步长为0.1。然后，我们将缩放后的图像输入测试模型，包括Inc-v3、Inc-v4、IncRes-2和Res-101，以获得超过1000张图像的平均损失。

如图1所示，我们可以很容易地观察到，当缩放尺寸在[0.1,1.3]范围内时，loss曲线是平滑稳定的。也就是说，原始图像和缩放图像的损失值非常相似。因此，我们假设深度模型的尺度不变特性保持在[0.1,1.3]范围内，我们利用尺度不变特性来优化输入图像的尺度副本上的对抗扰动。

4.3 攻击单个模型

在本小节中，我们将我们的SI-NI-FGSM分别与TIM、DIM和TI-DIM集成，并将扩展的黑盒攻击成功率与单模型设置下的baseline进行比较。如表1所示，我们的扩展方法在黑盒设定下始终优于基线攻击$10\%\sim 35\%$ ，在白盒设置下成功率接近100%。这表明，SI-NI-FGSM可以作为一种强有力的方法来提高对抗性样本的可转移性。

4.4 攻击集成模型

在（Liu et al., 2016）的工作之后，我们考虑通过同时攻击多个模型来展示我们的方法的性能。具体来说，我们分别使用TIM、SI-NI-TIM、DIM、SI-NI-DIM、TI-DIM和SI-NI-TI-DIM攻击具有相同集合权重的正常训练模型集合（包括Inc-v3、Inc-v4、INCRESRS-v2和Res-101）。

如表2所示，我们的方法提高了基线上所有实验的攻击成功率。总的来说，我们的方法在黑盒设定下始终比基线攻击高出$10\%\sim 30\%$。特别是，SI-NI-TI-DIM是SI-NI-FGSM与TI-DIM相结合的扩展，可以欺骗经过对抗训练的模型，平均成功率高达93.5%。结果表明，这些先进的经过对抗训练模型在SI-NI-TI-DIM的黑盒攻击下鲁棒性较差。

4.5 攻击其他前沿防御模型

除了正常训练的模型和对抗训练的模型之外，我们考虑量化我们的方法对其他高级防御的有效性，包括NIPS竞赛中的Top-3防御解决方案（high-level representation guided denoiser（HGD，RANK-1）），random resizing and padding（R&P，RANK-2）和rank-3 submission（NIPS-r3），以及最近提出的三种防御方法（feature distillation（FD），purifying perturbations via image compression model（ComDefense）和randomized smoothing（RS）。

我们将我们的SI-NI-TI-DIM与MI-FGSM和TI-DIM进行了比较，前者是2017年NIPS竞赛中排名第一的攻击方案，后者是最先进的攻击方案。我们首先通过分别使用MI-FGSM、TI-DIM和SI-NI-TI-DIM在集成模型上生成对抗样本，包括Inc-v3、Inc-v4、IncRes-v2和Res-101。然后，我们通过攻击这些防御方法来评估对抗样本。

如表3所示，我们的方法SI-NI-TI-DIM的平均攻击成功率为90.3%，超过了最先进的攻击大约14.7%。SI-NI-TI-DIM仅依靠对抗样本的可转移性，并对正常训练的模型进行攻击，就可以欺骗对抗训练后的模型和其他先进的防御机制，为开发更强大的深度学习模型提出了一个新的安全问题。SI-NI-TI-DIM产生的一些对抗样本如附录B所示。

4.6 further analysis

NI-FGSM与MI-FGSM的对比： 我们对NI-FGSM和MI-FGSM之间的差异进行了额外分析。对抗样本在Inc-v3上进行构造，迭代次数从4到16不等，然后转移攻击Inc-v4和INCRS-v2。如图2所示，在相同的迭代次数下，NI-FGSM的攻击成功率高于MI-FGSM。从另一个角度来看，NI-FGSM需要更少的迭代次数就能获得与MI-FGSM相同的攻击成功率。结果不仅表明，NI-FGSM具有更好的可转移性，而且还表明，NI-FGSM具有the property of looking ahead，可以加速对抗样本的生成。

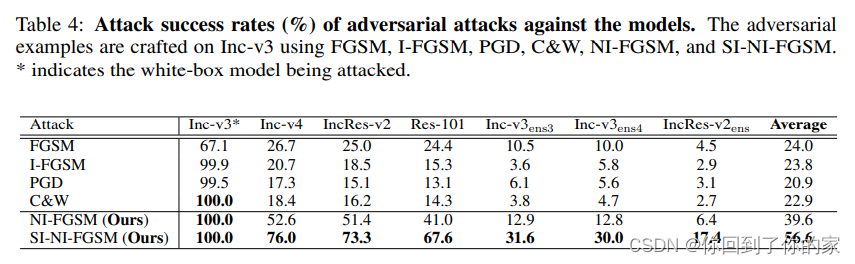
和传统方法的对比： 我们与经典攻击进行比较，包括FGSM，I-FGSM，PGD和C＆W。如表4所示，我们的方法实现了100%的攻击成功率，这与白盒设置下的C&W相同，并且显著优于黑盒设置下的其他方法。