信息与通信的数学基础——第十二章 分离变量法

1. 齐次方程问题

1. 定解问题：弦的自由振动

偏微分方程是线性齐次的、边界条件也是齐次的（双曲线类型）

流程：

（1）分离变量
令$u(x,t)=X(x)T(t)$，可得$X{T}^{\prime \prime }-a^2{X}^{\prime \prime }T=0$，令$\frac{T^{\prime \prime }}{a^{2}T}=\frac{X^{\prime \prime }}{X}=-\lambda$可得：

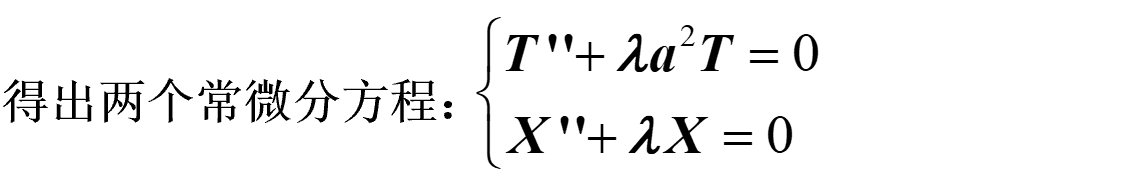
（2）求解本征值
特征方程为：$r^2+\lambda r=0$
① 当$\lambda <0,\lambda =0$时，方程只有零解，不合题意。
② 当$\lambda >0$时

$$X(x)=C_2\sin \frac{n\pi x}{l}$$
上解称为满足边界条件的固有解（特征解），$lambda$称为特征值，$\sin$函数为特征函数

（3）解出时间函数
将$\lambda$值带入常微分方程$T^{\prime \prime }+\lambda a^{2}T=0$可得：
$$\begin{gathered} T^{\prime \prime }+(\frac{n\pi a}{l}{)}^{2}T=0 \\ T(t)=A\cos \frac{n\pi a}{l}t+B\sin \frac{n\pi a}{l}t \end{gathered}$$

（4）得到一族解
$$u(x,t)=(A\cos \frac{n\pi a}{l}t+B\sin \frac{n\pi a}{l}t)\times C_2\sin \frac{n\pi x}{l}$$

例题1

（1）分离变量
假设$u(x,t)=X(x)T(t)$，带入方程可得：$X{T}^{\prime \prime }-a^2{X}^{\prime \prime }T=0$，令$\frac{T^{\prime \prime }}{a^{2}T}=\frac{X^{\prime \prime }}{X}=-\lambda$可得：
$$\begin{gathered} T^{\prime \prime }+\lambda a^{2}T=0 \\ {X}^{\prime \prime }+\lambda X=0 \end{gathered}$$
（2）求解本征值
对于方程$X{T}^{\prime \prime }-a^2{X}^{\prime \prime }T=0$，当$\lambda >0$时，方程存在非零解
因此方程的通解为：$X(x)=C_1\cos \sqrt{\lambda }x+C_2\sin \sqrt{\lambda }x$，带入初始条件可得：
① $u(x,t){|}_{x=0}=X(0)T(t)=0\to X(0)=0$
因此：$X(0)=C_1=0$
② $\frac{\partial u}{\partial x}{|}_{x=l}=0$
因此：$X^{\prime }=(-C_1\sin \sqrt{\lambda }x+C_2\cos \sqrt{\lambda }x){|}_{x=l}=C_2\cos \sqrt{\lambda }l=0$
$$\lambda =\frac{(2n+1{)}^2{\pi }^2}{4l^2}$$
（3）解出时间函数
将$\lambda$值带入常微分方程$T^{\prime \prime }+\lambda a^{2}T=0$可得：
$$\begin{gathered} T^{\prime \prime }+\frac{(2n+1{)}^2{\pi }^2}{4l^2}T=0 \\ T(t)=A\cos \frac{(2n+1)\pi }{2l}t+B\sin \frac{(2n+1)\pi }{2l}t \end{gathered}$$

（4）得到一族解
$$u(x,t)=(A\cos \frac{(2n+1)\pi }{2l}t+B\sin \frac{(2n+1)\pi }{2l}t)+C_2\cos \frac{(2n+1)\pi }{2l}x$$

2. 定解问题：有限长杆上的热传导

流程

（1）分离变量
假设$u(x,t)=X(x)T(t)$，带入方程可得：$X{T}^{\prime }-a^2{X}^{\prime \prime }T=0$，令$\frac{T^{\prime }}{a^{2}T}=\frac{X^{\prime \prime }}{X}=-\lambda$可得：
$$\begin{gathered} T^{\prime }+\lambda a^{2}T=0 \\ {X}^{\prime \prime }+\lambda X=0 \end{gathered}$$
（2）求解本征值
对于方程$X^{\prime \prime }+\lambda X=0$，当$\lambda >0$时，方程存在非零解
因此方程的通解为：$X(x)=C_1\cos \sqrt{\lambda }x+C_2\sin \sqrt{\lambda }x$，带入初始条件可得：
① $u(x,t){|}_{x=0}=X(0)T(t)=0\to X(0)=0$
因此：$X(0)=C_1=0$
② $u(x,t){|}_{x=l}=X(l)T(t)=0\to X(l)=0$
因此：$X(l)=C_1\cos \sqrt{\lambda }l+C_2\sin \sqrt{\lambda }l=0$
$$\lambda =(\frac{n\pi }{l}{)}^2$$
（3）解出时间函数
将$\lambda$值带入常微分方程$T^{\prime }+\lambda a^{2}T=0$可得：
$$\begin{gathered} T^{\prime }+(\frac{n\pi a}{l}{)}^2=0 \\ T(t)=D{e}^{-\frac{n^2{\pi }^2{a}^{2}t}{l^2}} \end{gathered}$$

（4）得到一族解
$$u(x,t)=A{e}^{-\frac{n^2{\pi }^2{a}^{2}t}{l^2}}\sin \frac{n\pi a}{l}x$$

齐次方程综合