线性代数:零空间维度等于自由变量个数的原因

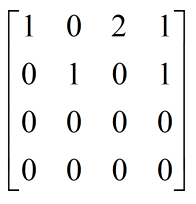
①以下展开的论述均以下图的矩阵为例

               

②上述矩阵特征: 2个主变量，2个自由变量

③该矩阵零空间的构成:

形式化的理解:在AX=0的条件下，对2个自由变量任意赋值，求得对应主变量的值，从而形成了零空间中的一个向量。在对2个自由变量分别赋完所有可能的值后，得到的向量的集合，形成了“零空间”

④零空间的特征以及零空间维度等于自由变量个数的原因

(1)对2个自由变量赋值，可以理解为在一个xoy平面上任取一点。其中，点的坐标分别对应两个不同的自由变量的取值。使2个自由变量分别赋完所有可能的值，等价于取遍整个xoy平面。

(2)当2个自由变量的值取遍整个平面，并分别求出相应主变量的值所组成的向量的集合(AX=0条件下)，形成了零空间

(3)欲完全覆盖整个二维平面，需要两个线性无关的向量作为基(这里是使矩阵各列线性组合为0的两组特解，也即2个自由变量随机取值求得主变量后所形成的向量)，然后对它们进行线性组合，即可得到一个二维平面。该二维平面涵盖了自由变量所有可能的取值，所以该平面为“零空间”

⑤总结

   本例中，有2个自由变量，所以在一个无限大的平面上承载了2个自由变量所有可能的取值。同理，如果有三个自由变量，则需要一个三维的空间来承载。以此类推，当有n个自由变量时，则需要一个n维的空间来承载n个自由变量的所有取值。而AX=0的所有解的集合生成了整个零空间，n个自由变量的所有可能取值对应了AX=0的所有解。所以零空间的维度等于自由变量的个数。