多元函数微分学之偏导数

今天又看了多元函数这一章，看到了自己的笔记，觉得不错分享下。都翻译成了自己的语言，真心反对书上的炫技和文绉绉的话。

• 偏导数的概念

本质上就是求一元函数的导，只不过是把其他变量看作常数就行了。

在图像上显示可以想象下，例如z=f(x，y)这是一个三维 图形，然后对x求偏导其实就这一点所在的平行于zx平面的切面是投影到z，x上的函数线条的导数，同样的对y求偏导就是放到了zy上看。

备注：看懂后面的再来看下面的、

 这就是为什么有求出一个一阶偏导数连续，但是不能说它一定连续，投在zx上是连续的，但是再zy上呢？可能就是断断续续的。

所以只有所有变量的偏导数都存在时，才能说时可微的。

 

• 几何意义

自己去看书或者百度，难敲。

• 多元函数连续、可导、可微之间的关系

   

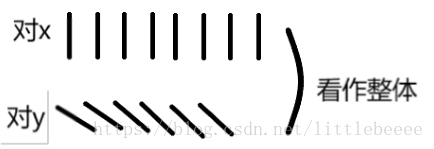
只对一个变量求导所以只有一排自行车        对多个变量求导这里以z=f(x，y)为例，所以两排

                                                        

连续不一定导                                                                                                   y这边导了，x没导，但他们是一个整体

                                                                         于是有可导不代表连续

导一定连续                                                                                                        连续不能让它导

这个想法挺有意思的，但记住熟练后完全可以丢掉了