ICP算法思想与推导详解——什么东西“最近点”，又“迭代”了什么？

一、什么是ICP

ICP的全称是 iterative closest point —— 迭代最近点。它是一种点云匹配的算法。

在三维重建或者视觉Slam场景中，经常需要确定某一时刻的相机位姿。
相机在运动过程中，不同时刻对同一物体获取的三维点云信息是不同的。
此时我们可以通过点云的对应点在两个时刻间差异来计算相机位姿的改变。
对位姿、相机模型等不了解的可以去看我的VSLAM笔记-相机模型。

简而言之，ICP目的就是为了使用某种方法求出两组点云之间的三维旋转与平移矩阵 $\mathbf{T}$

二、算法简介

2.1 场景

通常，我们可以使用一组空间点云数据来表示某一物体，记为 { p i } \{\boldsymbol p_i\} {pi​}
在某一时刻，该物体发生了移动与旋转，此时他的空间坐标发生了变化，也就是点云数据 { p i } \{\boldsymbol p_i\} {pi​} 的坐标全都发生了变化，新点云坐标记为 { q i } \{\boldsymbol q_i\} {qi​}
那么通过学习刚性物体的旋转平移我们可以知道，${\mathbf{p}}_i$ 和 ${\mathbf{q}}_i$ 之间存在一定关系：
$$\begin{gathered} {\mathbf{q}}_i=\mathbf{R}{\mathbf{p}}_i+\mathbf{t},i=1,2,\dots ,n \\ 或 \\ {\bar{\mathbf{q}}}_i=\mathbf{T}{\bar{\mathbf{p}}}_i,i=1,2,\dots ,n \end{gathered}$$

2.2 步骤过程

ICP算法的大致分为两步：

1. 匹配两个点云 $\mathbf{P}$ 与 $\mathbf{Q}$ ，找出对应的点
2. 求 $\mathbf{R},\mathbf{t}$

那么此时需要解决的两个问题就是：

• 问题① 如何查找两个点云之间的相匹配的对应点？
• 问题② 使用什么方法来求出 $\mathbf{R},\mathbf{t}$

---

对于问题①

从算法名 “迭代最近点” 我们不难看出，此算法解决第一个问题的基本思想是使用距离最近的点作为匹配点。
也就是遍历点云 $\mathbf{P}$ 中的所有点，计算它们与点云 $\mathbf{Q}$ 中每个点的距离，将距离最少的点作为其对应点。

例如查找 ${\mathbf{p}}_5$ 的对应点就是计算它与所有 $\mathbf{q}$ 的距离，找出距离最近的那个 $\mathbf{q}$：
$$\underset{{\mathbf{q}}_i}{\min }\{dist({\mathbf{p}}_5,{\mathbf{q}}_i)\}$$

时间复杂度为 $O(n^2)$

找到对应点后，就可以使用一定方法来找出最优的 $\mathbf{R},\mathbf{t}$

注意，这里之所以说是 “最优的” $\mathbf{R},\mathbf{t}$ 值，是因为使用最近点匹配方法找出的对应点往往不是真实对应的点：

求出来的 $\mathbf{R},\mathbf{t}$ 自然也不会是最终真正的值。

所以这个时候我们就需要“迭代”，第一次计算得出了一组当前最优的 $\mathbf{R},\mathbf{t}$ 值以后，可以将点云 $\mathbf{P}$ 经过$\mathbf{R}\mathbf{p}+\mathbf{t}$移动到 ${\mathbf{P}}^{\prime }$ 的位置（就离目标点云 $\mathbf{Q}$ 近了一些），此时，再对 新的点云 ${\mathbf{P}}^{\prime }$ 和 点云 $\mathbf{Q}$ 重复上面的两个步骤即可。

每次迭代都可以式 $\mathbf{P}$ 更加靠近 $\mathbf{Q}$ 直到收敛为止。

---

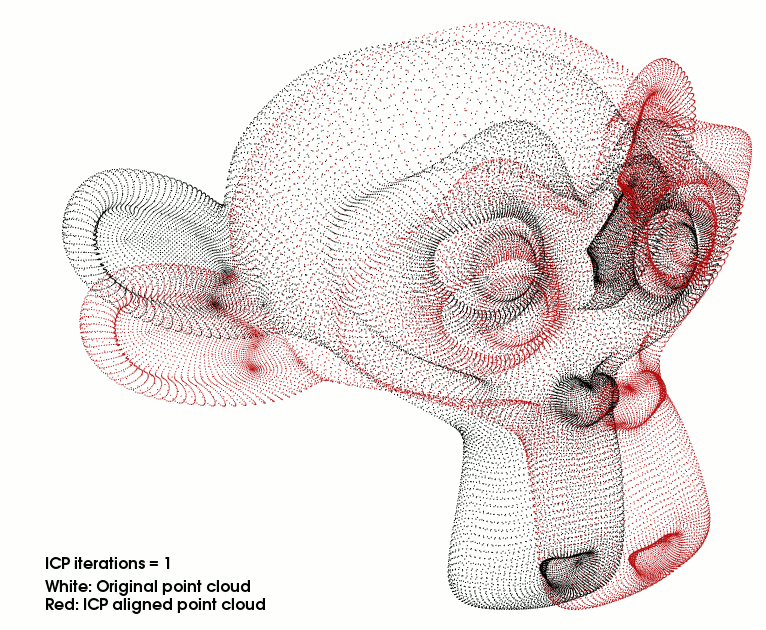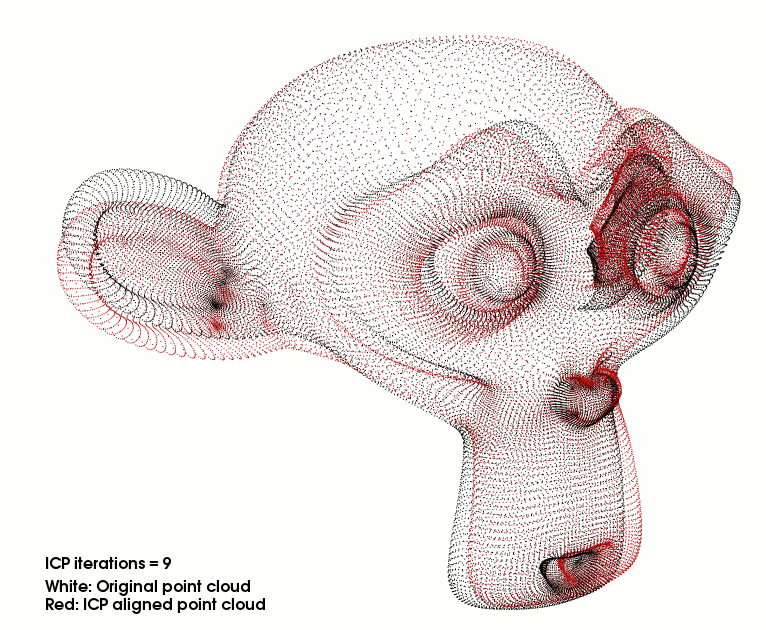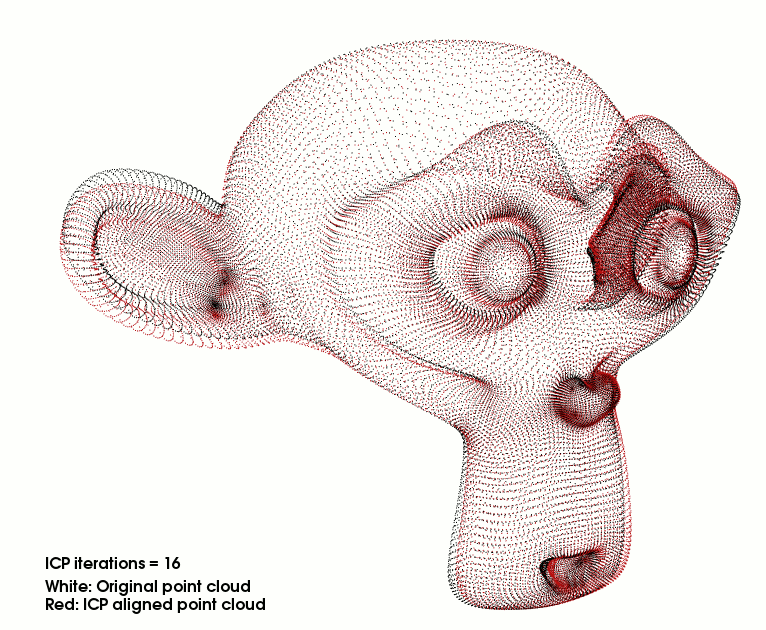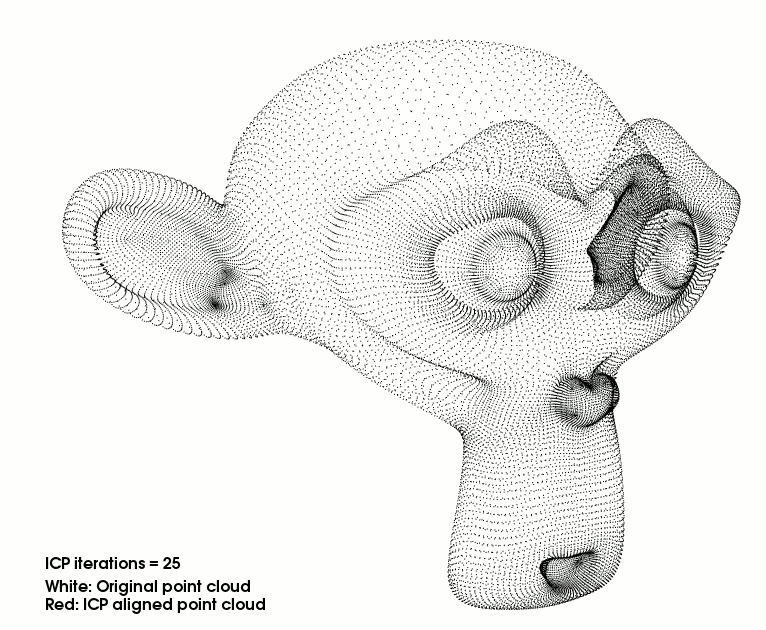
对于问题②

通过刚刚分析我们知道：
$${\mathbf{q}}_i\ne \mathbf{R}{\mathbf{p}}_i+\mathbf{t}$$
实际上：
$${\mathbf{q}}_i=\mathbf{R}{\mathbf{p}}_i+\mathbf{t}+{\mathbf{e}}_i$$
（此处是以 point-to-point 方法为例构造误差函数，其中 ${\mathbf{e}}_i$ 表示误差）

那么现在的任务其实就是使误差最小，即

$$\begin{gathered} \underset{\mathbf{R},\mathbf{t}}{\min }\sum _{i=1}^n|{\mathbf{q}}_i-\mathbf{R}{\mathbf{p}}_i-\mathbf{t}| \\ 或者 \\ \underset{\mathbf{R},\mathbf{t}}{\min }\frac{1}{2}\sum _{i=1}^n\Vert {\mathbf{q}}_i-\mathbf{R}{\mathbf{p}}_i-\mathbf{t}{\Vert }^2 \end{gathered}$$
再使用最小二乘等方式求解 $\mathbf{R},\mathbf{t}$ 即可

---

这里讲的是最基本的ICP算法的操作方法
其实对于上面两个问题的处理方法还有很多。

例如
对于问题①，除了使用最近点匹配，还可以使用投影坐标作为对应点匹配，或者融合RGB图像使用特征提取的方法来匹配等等；
对于问题②，常见的ICP构造误差函数的方法有Point-to-Point, Point-to-Plane, Plane-to-Plane等。

另外还有：

• 点太多了是不是可以采样选取？要如何采样？
• 是否可以对这些点添加一些权重来提高收敛速度？
• 有些差异过大的匹配点是否可以剔除掉？如何剔除？
  ……

等等许多问题也是很值得思考的。

ICP感觉是一个极其耗时的过程，所以按照使用场景选对每一步的方法很重要~
前几天刚看的 Kinect Fusion 使用的就是 投影坐标对应点匹配 + Point-to-Plane 方法来求解ICP的

三、$\mathbf{R},\mathbf{t}$ 求解推导

常用的求解方法有两种：

1. SVD求解法
2. 非线性优化

下面以 Point-to-Point ICP为例推导求解过程

2.1 使用SVD方法求解最优R与t

Point-to-Point 优化误差目标为：
$$\arg \underset{\mathbf{R},\mathbf{t}}{\min }\frac{1}{2}\sum _{i=1}^n\Vert {\mathbf{q}}_i-\mathbf{R}{\mathbf{p}}_i-\mathbf{t}{\Vert }^2$$

提一句：Point-to-Plane的目标函数为 $\arg \underset{\mathbf{R},\mathbf{t}}{\min }\frac{1}{2}\sum _{i=1}^n\Vert ({\mathbf{q}}_i-\mathbf{R}{\mathbf{p}}_i-\mathbf{t})\cdot {\mathbf{n}}_i{\Vert }^2$ ，其中 ${\mathbf{n}}_i$ 为法向量。有兴趣的可以自己查一下资料看看推导过程。

---

先求$\mathbf{t}$

记：
$$\mathbf{e}=\frac{1}{2}\sum _{i=1}^n\Vert {\mathbf{q}}_i-\mathbf{R}{\mathbf{p}}_i-\mathbf{t}{\Vert }^2$$
对$\mathbf{t}$求导：
$$\frac{\partial \mathbf{e}}{\partial \mathbf{t}}=-(\sum _{i=1}^n{\mathbf{q}}_i-\sum _{i=1}^n\mathbf{R}{\mathbf{p}}_i-n\mathbf{t})$$
令$\frac{\partial \mathbf{e}}{\partial \mathbf{t}}=0$得到：
$$\hat{\mathbf{t}}=\frac{1}{n}\sum _{i=1}^n{\mathbf{q}}_i-\mathbf{R}\cdot \frac{1}{n}\sum _{i=1}^n{\mathbf{p}}_i$$
分别记${\mathbf{\mu }}_q=\frac{1}{n}\sum _{i=1}^n{\mathbf{q}}_i,{\mathbf{\mu }}_p=\frac{1}{n}\sum _{i=1}^n{\mathbf{p}}_i$（很多地方也把它们称作点云的质心），那么上式就变为：
$$\hat{\mathbf{t}}={\mathbf{\mu }}_q-\mathbf{R}{\mathbf{\mu }}_p$$

---

再求$\mathbf{R}$

将 $\hat{\mathbf{t}}$ 带入原误差函数中得：
$$\begin{array}{rl}\mathbf{e}& =\frac{1}{2}\sum _{i=1}^n\Vert {\mathbf{q}}_i-\mathbf{R}{\mathbf{p}}_i-({\mathbf{\mu }}_q-\mathbf{R}{\mathbf{\mu }}_p){\Vert }^2\\ & =\frac{1}{2}\sum _{i=1}^n\Vert {\mathbf{q}}_i-{\mathbf{\mu }}_q-\mathbf{R}({\mathbf{p}}_i-{\mathbf{\mu }}_p){\Vert }^2\end{array}$$

再分别记${\mathbf{x}}_i={\mathbf{q}}_i-{\mathbf{\mu }}_q,{\mathbf{y}}_i={\mathbf{p}}_i-{\mathbf{\mu }}_p$ （相当于是每个点与其质心的距离，去中心化的操作） 得：
$$\mathbf{e}=\frac{1}{2}\sum _{i=1}^n\Vert {\mathbf{x}}_i-\mathbf{R}{\mathbf{y}}_i{\Vert }^2$$
所以：
$$\begin{array}{rl}\hat{\mathbf{R}}& =\arg \underset{\mathbf{R}}{\min }\sum _{i=1}^n\Vert {\mathbf{x}}_i-\mathbf{R}{\mathbf{y}}_i{\Vert }^2\\ & =\arg \underset{\mathbf{R}}{\min }\sum _{i=1}^n({\mathbf{x}}_i-\mathbf{R}{\mathbf{y}}_i{)}^{\mathrm{T}}({\mathbf{x}}_i-\mathbf{R}{\mathbf{y}}_i)\\ & =\arg \underset{\mathbf{R}}{\min }\sum _{i=1}^n({\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_i-{\mathbf{x}}_i^{\mathrm{T}}\mathbf{R}{\mathbf{y}}_i-{\mathbf{y}}_i^{\mathrm{T}}{\mathbf{R}}^{\mathrm{T}}{\mathbf{x}}_i-{\mathbf{y}}_i^{\mathrm{T}}{\mathbf{R}}^{\mathrm{T}}\mathbf{R}{\mathbf{y}}_i)\\ & =\arg \underset{\mathbf{R}}{\min }\sum _{i=1}^n({\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_i-2{\mathbf{x}}_i^{\mathrm{T}}\mathbf{R}{\mathbf{y}}_i-{\mathbf{y}}_i^{\mathrm{T}}{\mathbf{y}}_i)\\ & =\arg \underset{\mathbf{R}}{\max }\sum _{i=1}^n{\mathbf{x}}_i^{\mathrm{T}}\mathbf{R}{\mathbf{y}}_i\\ & =\arg \underset{\mathbf{R}}{\max }tr\left(\sum _{i=1}^n{\mathbf{x}}_i^{\mathrm{T}}\mathbf{R}{\mathbf{y}}_i\right)\\ & =\arg \underset{\mathbf{R}}{\max }tr\left(\sum _{i=1}^n\mathbf{R}{\mathbf{y}}_i{\mathbf{x}}_i^{\mathrm{T}}\right)\\ & =\arg \underset{\mathbf{R}}{\max }tr\left(\mathbf{R}\sum _{i=1}^n{\mathbf{y}}_i{\mathbf{x}}_i^{\mathrm{T}}\right)\end{array}$$

上面的 $tr$ 表示矩阵的迹
最后这个${\mathbf{y}}_i{\mathbf{x}}_i^{\mathrm{T}}$实际上是个协方差矩阵

记 $\mathbf{H}=\sum _{i=1}^n{\mathbf{y}}_i{\mathbf{x}}_i^{\mathrm{T}}$ ，有：
$$\hat{\mathbf{R}}=\arg \underset{\mathbf{R}}{\max }tr\left(\mathbf{R}\mathbf{H}\right)$$

现在对$\mathbf{H}$进行SVD分解可得：
$$\mathbf{H}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\mathrm{T}}$$
则：
$$\begin{array}{rl}\hat{\mathbf{R}}& =\arg \underset{\mathbf{R}}{\max }tr\left(\mathbf{R}\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\mathrm{T}}\right)\\ & =\arg \underset{\mathbf{R}}{\max }tr\left(\mathbf{\Sigma }{\mathbf{V}}^{\mathrm{T}}\mathbf{R}\mathbf{U}\right)\end{array}$$

记 $\mathbf{M}={\mathbf{V}}^{\mathrm{T}}\mathbf{R}\mathbf{U}$，又 $\mathbf{\Sigma }$ 是对角阵
那么：
$$\begin{array}{rl}\hat{\mathbf{R}}& =\arg \underset{\mathbf{R}}{\max }tr\left(\mathbf{\Sigma }\mathbf{M}\right)\\ & =\arg \underset{\mathbf{R}}{\max }tr\left(\sum _{i=1}^n{\sigma }_i{m}_{ii}\right)\end{array}$$

因为 ${\mathbf{V}}^{\mathrm{T}},\mathbf{R},\mathbf{U}$ 均为正交矩阵，所以$\mathbf{M}$是正交矩阵，则 $m_{ij}\le 1$
故当 $m_{ii}=1$ 时，$\sum _{i=1}^n{\sigma }_i{m}_{ii}$取到最大值。
而 $\mathbf{M}$ 是正交矩阵，所以
$$\mathbf{M}=\mathbf{I}$$
即
$${\mathbf{V}}^{\mathrm{T}}\mathbf{R}\mathbf{U}=\mathbf{I}$$
所以
$$\hat{\mathbf{R}}=\mathbf{V}{\mathbf{U}}^{\mathrm{T}}$$

至此，求得最优的 $\mathbf{R}$ 与 $\mathbf{t}$

2.2 使用非线性优化求解

此方法比较复杂，可以看我的VSLAM笔记-BundleAdjustment。

---

懒得写参考资料了，好麻烦 >.>