正态分布方法判别，独立样本T检验及Mann-Whitney U 检验操作

一个连续型变量数据是否符合正态分布，通常有以下两种情况：一种情况是数据本身整体的分布是否符合正态分布；另一种就是数据在某个分组上是否符合正态分布。

正态性校验

数据整体是否符合正态分布

检验数据本身整体是否符合正态分布

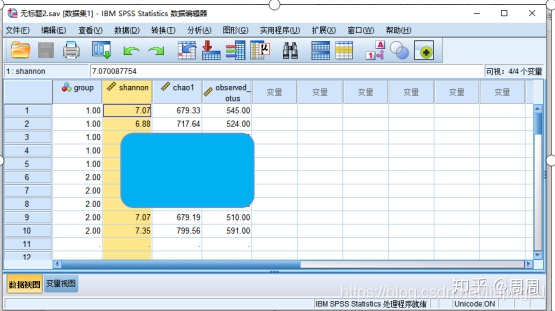
下面是为了分析菌群α多样性指数Chao1，Shannon以及observed_otus指数在正常和模型组之间有无显著性差异，所以需要先分析Shannon这一列数据是否符合正态分布（图1）

SPSS中的操作步骤

①依次点击：“分析”-“非参数检验”-“旧对话框”-“单样本K-S”（图2），在弹出的对话框中，将“年龄”选入右侧栏中，并在下方“检验分布”中勾选“正态”（图3）选项。然后点击确定。
②分析结果

从上方SPSS的输出结果可以看出：渐近显著性（双侧）为0.073大于0.05，意味着Shannon数据整体是符合正态分布的。

检验变量在某个分组上是否符合正态分布

还是用上面的案例，如果要比较不同组别的Shannon是否有差异，这时候就需要检验Shannon在不同组别上是否符合正态分布。

某分组上是否符合正态分布

在SPSS中，正态分布的检验方法有：计算偏度系数（Skewness）和峰度系数（Kurtosis）、Kolmogorov-Smirnov检验（KS检验或D检验）、Shapiro-Wilk（SW检验或W检验）、直方图、QQ图等。

SPSS中的操作步骤

①依次点击：“分析”-“描述统计”-“探索”

②在弹出的窗口中，将“Shannon”选入因变量列表，将“性别”选入“Group”列表

③设置参数，点击右侧的“图”按钮，勾选“含检验的正态图”，点击继续，再点击确定。

④结果分析，在结果界面点击左侧“正态性检验”标签，在右侧的正态性检验表中，看夏皮洛-威尔克那部分的显著性水平

此表，是对数据的统计描述，我们可以关注下偏度（Skewness）和峰度（Kurtosis）。
偏度SK越趋近0，数据越服从正态分布，众数=中位数=平均数；SK>0，为正偏态或左偏，众数<中位数<平均数；SK<0，为负偏态或右偏，众数>中位数>平均数。
峰度KG越趋近3，数据越服从正态分布；KG>3，峰度尖锐；KG<3，峰度扁平。（或exceess_KG=KG-3，exceess_KG越趋近0，数据越服从正态分布）
但是仅根据偏度和峰度还不足以判断数据是否服从正态分布，需要做进一步的检验。

由上图正态性校验可以看出1分组P>0.05，2分组P>0.05，**这里注意了：当所有分组的P都大于0.05，就能说是符合正态分布，