理解SLAM中的四元数基础知识

什么是四元数

　四元数(Quaternion)则是一种紧凑、易于迭代、又不会出现奇异值的表示方法。它在程序中广为使用，在学习SLAM过程中，对于初学者来说比较难理解的应该是这一部分知识了，因此，理解四元数的含义与用法，对学习SLAM来说是必须的。本节我们就来讲讲四元数，这里只是简单介绍四元数的基本用法以及在SLAM中公式推导会用到的几个重要推论，想要学SLAM的可以记下那几个推论，在SLAM理论推导中都会用到的。

　四元数是Hamilton找到的一种扩展的复数。一个四元数拥有一个实部和三个虚部：

                                                                                                                                           q = q0+q1i+q2j+q3k

其中i,j,k为四元数的三个虚部。这三个虚部满足关系式：

 由于它的这种特殊表示形式，有时人们也用一个标量和一个向量来表达四元数：

这里，标量s称为四元数的实部，而向量v称为它的虚部。如果一个四元数虚部为0，称之为实四元数。反之，若它的实部为0，称之为虚四元数。该定义和复数是相似的。这里需要说明一下，四元数表现形式有点混乱，四元数实部在前的是Hamilton，反之，实部在后的是JPL，JPL一般在航空领域用的比较多。

对于这两种四元数，可以看成左手系和右手系的区别，JPL是在随运动坐标系下观察绝对静止物体的相对位置，而Hamilton在全局坐标系下观察运动物体的空间变换。具体关系如下表：

这里先明确用Hamilton的四元数。四元数可以表示三维空间中任意一个旋转。与旋转矩阵中类似，我们仍假设某个旋转是绕单位向量n=[nx,ny,nz]T进行了角度为θ的旋转，那么这个旋转的四元数形式为：

事实上，这还是一个模长为1的四元数，称为单位四元数。反之，我们亦可通过任意一个长度为1的四元数，计算对应旋转轴与夹角：

若某个四元数长度不为1，我们可以通过归一化将它转换为一个模长为1的四元数。

对四元数的θ加上2π，我们得到一个相同的旋转，但此时对应的四元数变成了−q。因此，在四元数中，任意的旋转都可以由两个互为相反数的四元数表示。同理，取θ为0，则得到一个没有任何旋转的四元数：

四元数的基本运算

四元数和通常复数一样，可以进行一系列的运算。常见的有四则运算、内积、求逆、共轭、求指数／对数等等。表示姿态时，它还可以进行插值。下面我们分别介绍。

现有两个四元数qa,qb，它们的向量表示为[sa,va],[sb,vb]，或者原始四元数表示为：

那么，它们的运算可表示如下。

1.加法和减法

四元数qa,qb的加减运算为：

2.乘法

乘法是把qa的每一项与qb每项相乘，最后相加，具体如下：

虽然稍为复杂，但形式上也是整齐有序的。如果写成向量形式并利用内外积运算，该表达会更加简洁：

从公式中可以看出，最后一项是叉乘，叉乘存在方向，所以如果两个交换方向是不一样的，除非va和vb在R3中共线。否则乘法不可交换。

四元数乘法可以另写成矩阵形式，为此，我们先介绍矩阵叉乘符号，使用反对称运算，定义为：

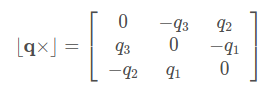
叉乘又可以表现为：

L和 R 的属性如下

其中矩阵 Ψ 和 Ξ 定义为

四元数有一个关于乘法中性的元素，定义为：

3 共轭

四元数的共轭为：

 即把虚部取成相反数。四元数共轭与自己本身相乘，会得到一个实四元数，其实部为模长的平方:

 4 模长

四元数的模长定义为：

 可以验证，两个四元数乘积的模即为模的乘积。这保证单位四元数相乘后仍是单位四元数。

5 逆

一个四元数的逆为：

按此定义，四元数和自己的逆的乘积为实四元数的1：

同时，乘积的逆有和矩阵相似的性质：

对于单位四元数，即||q||=1，它的逆即是它的共轭四元数。

6 数乘与点乘

和向量相似，四元数可以与数相乘：

点乘是指两个四元数每个位置上的数值分别相乘：

用四元数表示旋转

在复数域C，我们可以用一个复数表示2D的旋转，类似的，3D空间也可以用单位四元数表示旋转。假设一个空间三维点v=[x,y,z]∈R3，以及一个由旋转轴和夹角n,θ

给定一个旋转，如何用四元数表示它们？

首先，我们把三维空间点用一个虚四元数来描述：

然后，用另一个四元数q表示这个旋转：

那么，旋转后的点p′即可表示为这样的乘积：

可以验证，计算结果的实部为nT(n×v)=0，故计算结果为纯虚四元数。其虚部的三个分量表示旋转后3D点的坐标。

四元数到旋转矩阵的转换

由于任意单位四元数都可表示为一个3D旋转，即SO(3)中的元素，那么旋转矩阵和单位四元数之间是否存在转换关系，如何转换呢，这里给出一般的转换关系。

设四元数q=q0+q1i+q2j+q3k，对应的旋转矩阵R为：

反之，由旋转矩阵到四元数的转换如下。假设矩阵R={mij},i,j∈[1,2,3]，其对应的四元数q由下式给出：

事实上一个R的四元数表示并不是惟一的。存在其他三种与上式类似的计算方式。实际编程中，当q0接近0时，其余三个分量会非常大，导致解不稳定，此时会考虑使用剩下的几种方式计算。

其他几种变换

3D空间中的变换，除了欧氏变换之外，还存在其他几种变换（事实上欧氏变换是最简单的）。它们有一部分和测量几何有关，我们之后的讲解中会提到，在此先罗列出来。

1相似变换

相似变换比欧氏变换多了一个自由度，它允许物体进行自由地缩放。

注意到旋转部分多了一个缩放因子s，它在x,y,z三个坐标上形成均匀的缩放。类似的，相似变换的乘法也构成群，称为Sim(3)。由于含有缩放，相似变换不再保持图形的面积不变，一般用在回环检测。

2 仿射变换

仿射变换的矩阵形式如下：

与欧氏变换不同的是，仿射变换只要求A是一个可逆矩阵，而不必是正交矩阵。在仿射变换下，直线的夹角会发生改变，但平行性质不变。这即是说，仿射变换把平行四边形变为平行四边形。

3射影变换

射影变换是最一般的变换，它的矩阵形式为:

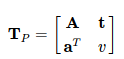
它左上角为可逆矩阵A，右上为平移t，左下缩放aT。由于采用齐坐标，当v≠0时，我们可以对整个矩阵除以v得到一个右下角为1的矩阵； 否则，则得到右下角为0的矩阵。因此，这个矩阵在2D中一共有8个自由度，而在3D中一共有15个自由度，是现在提到的变换中最为一般的。

下表总结了目前讲到的几种变换的性质。注意在“不变性质”中，从上到下是有包含关系的。例如，欧氏变换除了保体积之外，也具有保平行、相交等性质。

 这里再写几个个人感觉在SLAM中很有用的性质以及结论，这里不涉及推导：

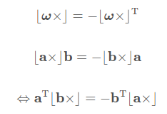
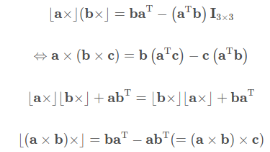
四元数（JPL）的微分：

四元数（JPL）的零阶积分

在短的陀螺采样周期中，认为角速度w恒定。构造等效旋转矢量：

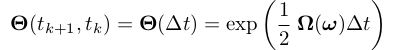
则零阶积分可以为：

当更新周期极短时(w极小<10e-5)，使用LHopital法则进行更新：