四元数——基本概念。SLAM中理解，二阶 四阶矩阵表示

四元数——基本概念

四元数系列：

四元数——基本概念

四元数——旋转

四元数应用——转矩阵、Slerp插值与万向节

四元数应用——顺序无关的旋转混合

—————————————————————————————————————————

导语：相比矩阵，用四元数处理3D旋转的优势是毋庸置疑的，但由于概念复杂，难于理解，一直是我最头疼的问题。最近忙里偷闲，翻了些材料，感觉醍醐灌醒、豁然开朗，这里写点心得，也就抛个砖，引个玉，希望能帮到和我一样困惑的人。

0.先甩干货

不得不说，目前国内了解这方面知识的渠道少之又少。知乎上也有类似问题——如何形象地理解四元数，干货私货一大堆。这里先推荐两个比较有用的资料，算是相辅相成。搞懂了这些，我觉得针对图形学来说就差不多够用了。

首先推荐一本书《Visualizing Quaternions》。这书算是本数学书，不过里面也有不少实现代码，估计受众就是程序员。本书顾名思义，主要介绍如何将四元数可视化，所以全书主要重心是研究四元数各种几何意义，虽然提到旋转，但并没有牵扯一个核心问题，如何用单位四元数去旋转一个三维向量，好在介绍这个的文章一抓一大把。这本书也不需要都看，我是挑着看的，个人觉得通读30%-40%的内容就够用了，其余部分比较复杂，内容也比较深，可以有需求针对翻阅。顺带一提国内此书价格一般在1000+，而美亚二手书一般60-70刀，喜欢收实体书的可以参考一下。

下面推荐一篇文章《Understanding Quaternions》，这篇文章相比

大多数技术博客来说，写的已经非常全面详尽。但是对于复数和四元数的关联，四元数的指数对数运算，还有一些四元数的理解显然由于篇幅原因没有说的太清晰，个人觉得这部分参考上面推荐的书就行了，该文章最核心的部分在于对旋转的描述，通过实例，极为清晰地介绍了四元数怎么去旋转一个三维向量。下面给出文章的链接。

英文原版：Understanding Quaternions 中文翻译：理解四元数

最后推荐另一本书《Quaternions For Computer Graphics》。上面的文章主要引用自这本书，这本书对于四元数如何应用于旋转，从原理到实践都说的非常详细，正好弥补第一本书籍的不足。而且《Understanding Quaternions》有部分也说的不是很明白，但都能在这本书上面找到对应的解释。

这里说一下，其实上面两本读物就已经够了。本文拟了这篇文章，更多是给自己写个归纳笔记，可能大多以概念体会为主，而不是传统意义上的手把手教程。所以，尽量还是以推荐的干货读物为主，许多基础的公式推算本文是不涉及的。

1.为什么要用四元数

可能四元数的由来大家都看过很多遍。很久以前，一位老者坐在大桥边上，看着过往船只，突然灵光一闪，在桥边石碑上洋洋洒洒刻上几行大字，四元数诞生了！故事大家都爱听，那么为什么我们需要四元数？一种说法是解决向量乘法，我们知道向量之间乘法有内积和外积，但这两个运算均不完美，即不满足群的条件（当然四元数诞生的时候也还没有内积外积的说法）。那向量之间是否存在这样一个非常完美的乘法，于是三维空间无法解决的问题就映射到四维空间。这便是四元数诞生的契机。

那么问题又来了，既然四元数只是为了解决矩阵乘法，那为什么我们现在要用四元数进行旋转，甚至替代了欧拉角、轴角等形式？首先，四元数并不是生来为了解决三维旋转，而是它的性质非常有利于表达旋转信息（后面会详述），所以了解四元数的性质要先于了解四元数在旋转中的应用。至于四元数替代欧拉角等形式，就需要牵扯到一些别的知识点，我先罗列一下四元数相比其他形式的优点：

解决万向节死锁（Gimbal Lock）问题

仅需存储4个浮点数，相比矩阵更加轻量

四元数无论是求逆、串联等操作，相比矩阵更加高效

所以综合考虑，现在主流游戏或动画引擎都会以缩放向量+旋转四元数+平移向量的形式进行存储角色的运动数据。

2.四元数是怎么想出来的

平庸的教程会直接提出四元数的定义、运算规则等等，然后读者不知所云。相反，较为系统的教程一般会从复数（Complex Number）进行引导，逐步提出四元数的定义，这样会让读者更容易理解，在脑中也更好形成画面。那复数与四元数之间的关系、以及如何从复数这样一个概念扩展到四元数是我们需要理清的一个思路。

先说几个概念。

空间中的子空间：一般而言，空间（维度>2）都存在更低维的子空间，比如二维空间中一维子空间，也就是直线；三维空间中的一维子空间和二维子空间，也就是直线和面。当超过三维的概念我们就很难去想象是什么样子，但四维空间一定会存在三维子空间或二维子空间。我们这里会加一个前缀超（hyper）来形容这些空间，比如高维空间中的平面我们称为超平面。

空间和子空间的映射：我们将二维空间表示为(x,y)，当y=0时，其实可以看成是一维的，只不过它表示成(x,0)这种形式。推到四维，(w,x,y,z)，当w=0时，(0,x,y,z)就是一个三维子空间，这也是为什么我们可以用单位四元数对三维向量进行操作，其实我们是将三维向量映射到四维的三维子空间（w=0，这种形式也成纯四元数），然后对其进行旋转，最终得到的向量结果依然是这个三维子空间中的，因而可以映射回三维空间。

广义球：这里的球是广义上的。我们在二维平面上，广义球其实指代circle，三维空间上就是我们认知上的球，称为two-sphere，而四维空间中广义球其实是一个超球（hyper-sphere），又称为three-sphere。单位向量其实就是广义球上面的点，而单位四元数也就是three-sphere上面的点。

约束与特征向量：空间中的一点由x, y, z等参数来表示，一般来说参数的数量与维数相等，二维空间的点用{x, y}参数，四维空间的点用{x, y, z, w}参数。但是对于空间的点加以约束，则该会减少参数的数量，比如三维空间的点在某一单位球面上，原本三个参数{x, y, z}才能表达的点现在只需要两个参数{u, v}就可以表达。如果{u, v}是单位向量，也可以称{u, v}是{x, y, z}的特征向量。

上述概念给了大家一个思路，四元数这样一个东西并不是一蹴而就的，从空间来说，它与我们熟知的低维空间本质上是没有区别的，或者说是有很大共性的。四元数的很多特性都是从低维拓展而来的，更具体的说是从复数这一概念拓展的。

那什么是复数？

复数概念很简单，它其实就是为了满足数学家的强迫症，-1的平方根要有意义。看似很没有意义的复数，在实际中却用处非凡。我们首先看一下它的几何表达形式，令x为实部，y为虚部，则x+iy可以表示为下图。

复数的提出将原本一维的数值范围直接加了一个维度，数据量的增幅可以说是巨大的。那我们从极坐标的角度去思考复数，x+i·y可以写成r·cosθ+i·r·sinθ，我们只考虑单位复数，|r|=1，也就得到cosθ+i·sinθ。说到这，就要提一个代数学中常用的公式——欧拉公式，基本上复数的所有运算推到都会用到这个公式。

接下来我先不说复数的乘法，单位复数乘法可以达到一个二维旋转的效果，有兴趣的可以在这里画一画，推一推。我先介绍如何从复数推导出四元数，正如复数是有一个实部和一个虚部组成的，那我们将一个虚部换成三个虚部，即两两相交{i, j, k}。

其中n为三维的单位向量，i²=j²=k²=i·j·k=-1。这便是四元数的常规表达形式，不过单位四元数是有一大堆的约束的，并不是所有四维向量都是四元数。

这里再开一个脑洞，可能大家听说四元数、八元数，但是存在三元数、五元数？其实从客观上说，三元数、四元数、n元数都是存在的（也就是复数存在无穷个等级），但并不是所有的数系都满足模运算。而且随着维度的提高，特性会逐步牺牲，相比复数运算，四元数牺牲了交换律；相比四元数运算，八元数牺牲了结合律。当然也还存在十六元数，不过十六元数的特性将更少，在数学中也就更加没有意义，所以目前就四元数的应用最为广泛。

3.如何去理解四元数

现在我们总结一下已经得出的四元数特性：

四元数（以后不特指四元数=单位四元数）是四维空间中一个超球上面的点，满足w²+x²+y²+z²=1；而纯四元数是四维空间在w=0时的一个子空间的点，形式为{0, q}，特别注意的是纯四元数与四元数是不同的概念。

四元数是复数虚部扩展的结果，复数的虚部为1个，而四元数虚部有3个，且两两互相正交，其中实部是cosθ/2，而虚部为一个単位轴乘以sinθ/2。

四元数自由度并没有四个维度，由于存在w²+x²+y²+z²=1这个约束，它的自由度其实只有3，且每个四元数可以对应一个特征向量，即n。但请记住四元数并不是与特征向量一一对应的，后文会有说。

由于四元数存在于四维空间，所以如何利用低维信息去理解高维信息就显得尤为重要。我们这里先用三维举个例子，三维的球用代数表示为x²+y²+z²=1，虽然球上面的点是由x，y，z三个参数来确定，但实际上我们只需要两个。假设取x和z表示，其中y可以通过x和z进行求解。那么，我们将y轴信息给隐去，只看投影平面，如下图所示。这张图的意思是，整个球在XOZ平面上投影是一个圆，当球面一点投影在圆上时，y=0；投影的位置位于圆内时，则分别两种情况，y>0处于北半球，y<0处于南半球。所以我们仅通过投影后的圆即可还原出整个球体。

让我们推广到四维，w²+x²+y²+z²=1中取x、y和z来表示超球。如下图所示，四维空间投影到三维超平面（w=0）可能是一个two-sphere。当投影点在整个two-sphere的边缘时，w一定为0，值得一提的是在这个空间内的四元数是一个纯四元数。当投影点落在two-sphere的内部时，也分为两种情况，w>0和w<0。但是我们可以发现这两种情况下对应的特征向量是一样的，所以我们将旋转矩阵向四元数转换时，是有两个对应值的，四元数的范围是2倍覆盖于3D旋转（2:1 mapping）。

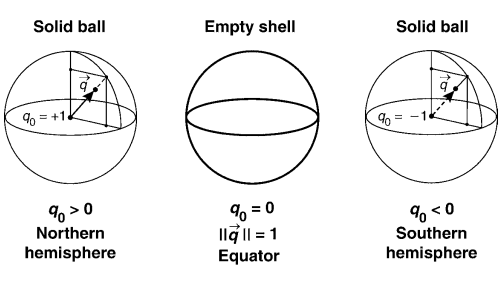
上面两段写的相对来说比较玄乎，但我觉得可以对理解四维空间和四元数相当有帮助。本文表述能力有限，如果实在看不懂的，可以翻阅《Visualizing Quaternions》第八章，个人觉得这是书中最为精彩的部分之一。

4.四元数的“乘法”运算

前文提到了四元数之间的“乘法”规则是满足群的性质，那究竟是怎样的乘法，又是怎么满足的，接下来我们一起来看一看。

由于四元数有i，j，k三个虚部，所以得满足i²=j²=k²=i·j·k=-1这个条件。这里令★为“乘法”操作符，则p★q的公式如下，具体的推导步骤我就不写了。

我们首先针对单位四元数，按照群的性质一条条过：

封闭性：易证明，p和p的共轭相乘即可，|p★q|=1。

结合律：这条也很好证明，只要证明(p★q)★r=p★(q★r)。

以上两个证明这里就不详述了，毕竟知乎也不好编辑公式。我们可以换种思路，从几何的角度思考，由于单位四元数旋转后还是单位四元数，所以满足封闭性。同时，类比矩阵乘法，单位四元数也应该满足结合律。

单位元素：e=(1,0,0,0)，这也是四元数的一个初始值（相当于单位矩阵）。带入上面的公式可知，p★(1,0,0,0)还是等于p。

逆元素：p存在一单位四元数，★操作的结果为e，具体参考下面公式，可以看出逆元素就是其共轭除以模的平方。

如果这里是复数，可能还会满足交换律，就是一个阿贝尔群。但四元数肯定不满足交换律，无论从代数的角度，还是从几何角度。到这里，基本也就介绍完了四元数的乘法运算，如果用其指数形式（exp形式），证明这些性质就会更简单。

5.四元数的指数、对数与内积

根据欧拉公式可知，四元数的指数形式只是换了一种表达方式，都是表达同一个东西。而其对数形式也就是四元数指数形式的指数，如下图公式所示。这对公式在计算四元数插值的时候很有用，这个后文再说。

那么对数和指数的关系是什么呢？我们参考下图，其实对数的变化量其实就是角度的大小，所以用下图可以很直观的看出四元数指数形式和对数形式之间的关系。

最后介绍一下四元数的内积。我们先看三维空间或二维空间，如果两个单位向量算内积，内积的结果为两个向量的夹角。四元数也是如此，两个单位四元数的内积就是其夹角，这个结论推广到n维也是成立，原因很简单，因为三点共面，即使n维空间，两个向量所在的空间也仅是二维子空间。至于外积，由于对于复数和四元数来说，外积的意义均不是很明显，这里就不做过多讨论。

关于旋转部分就下次再说吧！

https://zhuanlan.zhihu.com/p/27471300

理解SLAM中的四元数基础知识

什么是四元数

　四元数(Quaternion)则是一种紧凑、易于迭代、又不会出现奇异值的表示方法。它在程序中广为使用，在学习SLAM过程中，对于初学者来说比较难理解的应该是这一部分知识了，因此，理解四元数的含义与用法，对学习SLAM来说是必须的。本节我们就来讲讲四元数，这里只是简单介绍四元数的基本用法以及在SLAM中公式推导会用到的几个重要推论，想要学SLAM的可以记下那几个推论，在SLAM理论推导中都会用到的。

　四元数是Hamilton找到的一种扩展的复数。一个四元数拥有一个实部和三个虚部：

q = q0+q1i+q2j+q3k

其中i,j,k为四元数的三个虚部。这三个虚部满足关系式：

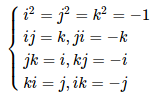
由于它的这种特殊表示形式，有时人们也用一个标量和一个向量来表达四元数：

这里，标量s称为四元数的实部，而向量v称为它的虚部。如果一个四元数虚部为0，称之为实四元数。反之，若它的实部为0，称之为虚四元数。该定义和复数是相似的。这里需要说明一下，四元数表现形式有点混乱，四元数实部在前的是Hamilton，反之，实部在后的是JPL，JPL一般在航空领域用的比较多。

对于这两种四元数，可以看成左手系和右手系的区别，JPL是在随运动坐标系下观察绝对静止物体的相对位置，而Hamilton在全局坐标系下观察运动物体的空间变换。具体关系如下表：

这里先明确用Hamilton的四元数。四元数可以表示三维空间中任意一个旋转。与旋转矩阵中类似，我们仍假设某个旋转是绕单位向量n=[nx,ny,nz]T进行了角度为θ的旋转，那么这个旋转的四元数形式为：

事实上，这还是一个模长为1的四元数，称为单位四元数。反之，我们亦可通过任意一个长度为1的四元数，计算对应旋转轴与夹角：

若某个四元数长度不为1，我们可以通过归一化将它转换为一个模长为1的四元数。

对四元数的θ加上2π，我们得到一个相同的旋转，但此时对应的四元数变成了−q。因此，在四元数中，任意的旋转都可以由两个互为相反数的四元数表示。同理，取θ为0，则得到一个没有任何旋转的四元数：

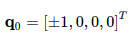
四元数的基本运算

四元数和通常复数一样，可以进行一系列的运算。常见的有四则运算、内积、求逆、共轭、求指数／对数等等。表示姿态时，它还可以进行插值。下面我们分别介绍。

现有两个四元数qa,qb，它们的向量表示为[sa,va],[sb,vb]，或者原始四元数表示为：

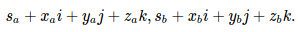
那么，它们的运算可表示如下。

1.加法和减法

四元数qa,qb的加减运算为：

2.乘法

乘法是把qa的每一项与qb每项相乘，最后相加，具体如下：

虽然稍为复杂，但形式上也是整齐有序的。如果写成向量形式并利用内外积运算，该表达会更加简洁：

从公式中可以看出，最后一项是叉乘，叉乘存在方向，所以如果两个交换方向是不一样的，除非va和vb在R3中共线。否则乘法不可交换。

四元数乘法可以另写成矩阵形式，为此，我们先介绍矩阵叉乘符号，使用反对称运算，定义为：

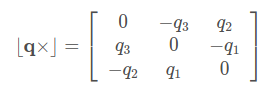
叉乘又可以表现为：

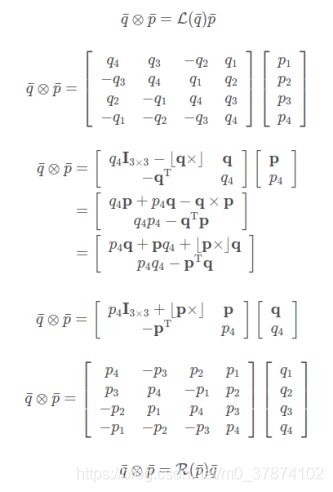
L和 R 的属性如下

其中矩阵 Ψ 和 Ξ 定义为

四元数有一个关于乘法中性的元素，定义为：

3 共轭

四元数的共轭为：

即把虚部取成相反数。四元数共轭与自己本身相乘，会得到一个实四元数，其实部为模长的平方:

4 模长

四元数的模长定义为：

可以验证，两个四元数乘积的模即为模的乘积。这保证单位四元数相乘后仍是单位四元数

5 逆

一个四元数的逆为：

按此定义，四元数和自己的逆的乘积为实四元数的1：

同时，乘积的逆有和矩阵相似的性质：

对于单位四元数，即||q||=1，它的逆即是它的共轭四元数。

6 数乘与点乘

和向量相似，四元数可以与数相乘：

点乘是指两个四元数每个位置上的数值分别相乘：

用四元数表示旋转

在复数域C，我们可以用一个复数表示2D的旋转，类似的，3D空间也可以用单位四元数表示旋转。假设一个空间三维点v=[x,y,z]∈R3，以及一个由旋转轴和夹角n,θ

给定一个旋转，如何用四元数表示它们？

首先，我们把三维空间点用一个虚四元数来描述：

然后，用另一个四元数q表示这个旋转：

那么，旋转后的点p′即可表示为这样的乘积：

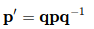
可以验证，计算结果的实部为nT(n×v)=0，故计算结果为纯虚四元数。其虚部的三个分量表示旋转后3D点的坐标。

四元数到旋转矩阵的转换

由于任意单位四元数都可表示为一个3D旋转，即SO(3)中的元素，那么旋转矩阵和单位四元数之间是否存在转换关系，如何转换呢，这里给出一般的转换关系。

设四元数q=q0+q1i+q2j+q3k，对应的旋转矩阵R为：

反之，由旋转矩阵到四元数的转换如下。假设矩阵R={mij},i,j∈[1,2,3]，其对应的四元数q由下式给出：

事实上一个R的四元数表示并不是惟一的。存在其他三种与上式类似的计算方式。实际编程中，当q0接近0时，其余三个分量会非常大，导致解不稳定，此时会考虑使用剩下的几种方式计算。

其他几种变换

3D空间中的变换，除了欧氏变换之外，还存在其他几种变换（事实上欧氏变换是最简单的）。它们有一部分和测量几何有关，我们之后的讲解中会提到，在此先罗列出来。

1相似变换

相似变换比欧氏变换多了一个自由度，它允许物体进行自由地缩放。

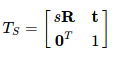
注意到旋转部分多了一个缩放因子s，它在x,y,z三个坐标上形成均匀的缩放。类似的，相似变换的乘法也构成群，称为Sim(3)。由于含有缩放，相似变换不再保持图形的面积不变，一般用在回环检测。

2 仿射变换

仿射变换的矩阵形式如下：

与欧氏变换不同的是，仿射变换只要求A是一个可逆矩阵，而不必是正交矩阵。在仿射变换下，直线的夹角会发生改变，但平行性质不变。这即是说，仿射变换把平行四边形变为平行四边形。

3射影变换

射影变换是最一般的变换，它的矩阵形式为:

它左上角为可逆矩阵A，右上为平移t，左下缩放aT。由于采用齐坐标，当v≠0时，我们可以对整个矩阵除以v得到一个右下角为1的矩阵； 否则，则得到右下角为0的矩阵。因此，这个矩阵在2D中一共有8个自由度，而在3D中一共有15个自由度，是现在提到的变换中最为一般的。

下表总结了目前讲到的几种变换的性质。注意在“不变性质”中，从上到下是有包含关系的。例如，欧氏变换除了保体积之外，也具有保平行、相交等性质。

这里再写几个个人感觉在SLAM中很有用的性质以及结论，这里不涉及推导：

四元数（JPL）的微分：

四元数（JPL）的零阶积分

在短的陀螺采样周期中，认为角速度w恒定。构造等效旋转矢量：

则零阶积分可以为：

当更新周期极短时(w极小<10e-5)，使用LHopital法则进行更新：

————————————————

版权声明：本文为CSDN博主「半不闲居士」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。

原文链接：https://blog.csdn.net/m0_37874102/article/details/114847374

四元数的理解（简单入门应用）

1.基本定义：

首先明确，四元数是超复数。

复数是什么呢？

复数是由实数加上虚数单位 i 组成，其中i^2 = -1。

四元数都是由实数加上三个虚数单位 i、j、k 组成，而且它们有如下的关系：

i^2 = j^2 = k^2 = -1， i^0 = j^0 = k^0 = 1

每个四元数都是 1、i、j 和 k 的线性组合，即是四元数一般可表示为a + bi+ cj + dk，其中a、b、c 、d是实数。

2.几何意义：

对于i、j、k本身的几何意义可以理解为一种旋转，其中：

i旋转代表X轴与Y轴相交平面中X轴正向向Y轴正向的旋转

j旋转代表Z轴与X轴相交平面中Z轴正向向X轴正向的旋转

k旋转代表Y轴与Z轴相交平面中Y轴正向向Z轴正向的旋转

-i、-j、-k分别代表i、j、k旋转的反向旋转。

3.矩阵表示:

四元数可以由矩阵表示，这便于将矩阵的加法、乘法应用于四元数的加、乘。

四元数的矩阵表示有两种：

1. 第一种是以二阶复数矩阵表示。

若 h = a + bi + cj + dk 则它的复数形式为：

这种表示法有如下优点：

所有复数 (c = d = 0) 就相应于一个实矩阵。

四元数的绝对值的平方就等于矩阵的行列式。

四元数的共轭值就等于矩阵的共轭转置。

2. 第二种则是以四阶实数矩阵表示：

其中四元数的共轭等于矩阵的转置。

4.基本运算：

百度百科介绍的很详细了，需要注意的就是，四元数乘法非可换

5.旋转跳跃，我不停歇

从之前四元数的几何意义就可以看出，其在旋转领域独树一帜。

空间坐标变换无非是平移、缩放和旋转，旋转应该是其中最复杂的变换。

旋转的表示，主要有三种：矩阵旋转、欧拉旋转和本文的四元数旋转。

下面对比一下这三种旋转方式的优缺点：

1.矩阵旋转

优点：

旋转轴可以是任意向量；

缺点：

旋转其实只需要知道一个向量+一个角度，一共4个值的信息，但矩阵法却使用了16个元素；

而且在做乘法操作时也会增加计算量，造成了空间和时间上的一些浪费

2.欧拉旋转

优点：

很容易理解，形象直观；

表示更方便，只需要3个值（分别对应x、y、z轴的旋转角度）；但按我的理解，它还是转换到了3个3*3的矩阵做变换，效率不如四元数；

缺点：

这种方法是要按照一个固定的坐标轴的顺序旋转的，因此不同的顺序会造成不同的结果；

会造成万向节锁（Gimbal Lock）的现象。这种现象的发生就是由于上述固定坐标轴旋转顺序造成的。理论上，欧拉旋转可以靠这种顺序让一个物体指到任何一个想要的方向，但如果在旋转中不幸让某些坐标轴重合了就会发生万向节锁，这时就会丢失一个方向上的旋转能力，也就是说在这种状态下我们无论怎么旋转（当然还是要原先的顺序）都不可能得到某些想要的旋转效果，除非我们打破原先的旋转顺序或者同时旋转3个坐标轴。具体可看视频了解。

由于万向节锁的存在，欧拉旋转无法实现球面平滑插值；

3.四元数旋转

优点：

可以避免万向节锁现象；

只需要一个4维的四元数就可以执行绕任意过原点的向量的旋转，方便快捷，在某些实现下比旋转矩阵效率更高；

可以提供平滑插值；

缺点：

比欧拉旋转稍微复杂了一点点，因为多了一个维度；

理解更困难，不直观；

理解层面感觉到这就可以了，简单的推导和旋转的表达可以参考该文章（基础好的之间从第4节开始），简单的应用参考该文章，旋转矩阵求解参考该文章，真正应用时，都有现成的模板和算法，甚至你不需要知道什么，只要知道你应输入的参数，和接收的结果就行了（个人感觉这方面研究到天花板了，我等凡人没必要深究）。

————————————————

版权声明：本文为CSDN博主「人工智睿」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。

原文链接：https://blog.csdn.net/weixin_44671418/article/details/107160366