贝叶斯统计：变分推断小总结

Abstract

变分推断是贝叶斯近似推断方法中的一大类方法，将后验推断问题巧妙地转化为优化问题进行求解。而马尔科夫蒙特卡洛（MCMC）采样也是近似推断的一种重要方法，其改进包括Metropolis-Hastings算法，Gibbs采样。在MCMC不满足性能要求的时候，我们使用变分推断。MCMC通过采样逼近后验，而变分推断通过优化逼近后验。

Introduction

贝叶斯统计推断主要有两大类方法，一类是精确推断方法，另一类是近似推断方法。精确推断方法通常需要很大的计算开销，因此在现实应用中近似推断方法更为常用。
近似推断方法大致可分为两类：第一类是马尔科夫方法，这种方法通过使用随机化方法完成近似；第二类是非马尔科夫方法，它使用确定性近似完成近似推断，典型代表为变分推断方法。
马尔科夫方法相较于变分法计算上消耗更大，但是它可以保证取得与目标分布相同的样本，而变分法没有这个保证：它只能寻找到近似于目标分布一个密度分布，但同时变分法计算上更快，由于我们将其转化为了优化问题，所以可以利用诸如随机优化或分布优化等方法快速的得到结果。所以当数据量较小时，我们可以用MCMC方法消耗更多的计算力但得到更精确的样本。当数据量较大时，我们用变分法处理比较合适。
Method
KL散度
用一个分布去拟合另一个分布通常需要衡量这两个分布之间的相似性，通常采用KL散度，下面简单介绍一下KL散度：
  机器学习中比较重要的一个概念—相对熵。相对熵又被称为KL散度或信息散度，是两个概率分布间差异的非对称性度量。在信息论中，相对熵等价于两个概率分布的信息熵的差值，若其中一个概率分布为真实分布，另一个为理论分布，则此时相对熵等于交叉熵与真实分布的信息熵之差，表示使用理论分布拟合真实分布时产生的信息损耗。其公式如下：
  
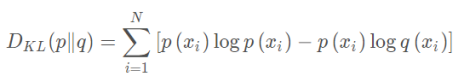
合并之后表示为：

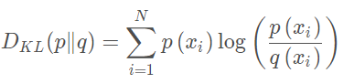
假设理论拟合出来的事件概率分布q(x)跟真实的分布p(x)一模一样，即p(x)=q(x)，那么p(xi)logq(xi)就等于真实事件的信息熵。在理论拟合出来的事件概率分布跟真实的一模一样的时候，相对熵等于0。而拟合出来不太一样的时候，相对熵大于0。其证明如下：

其中第一个不等式是由l n ( x )≤x−1推导出来的，只在p ( x i ) = q ( x i )时取到等号。这是深度学习梯度下降法需要的特性。假设神经网络拟合完美了，那么它就不再梯度下降，而不完美则因为它大于0而继续下降。但它具有不对称性，即用P来拟合Q和用Q来拟合 P的相对熵不一样，而他们的距离是一样的。这也就是说，相对熵的大小并不跟距离有一一对应的关系。

变分贝叶斯

我们经常利用贝叶斯公式求P(Z∣X)

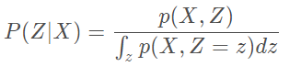
但P(Z | X)求解用贝叶斯的方法是比较困难的，因为我们需要去计算∫ z p ( X = x , Z = z ) d z，而Z通常会是一个高维的随机变量，这个积分计算起来就非常困难。在贝叶斯统计中，所有的对于未知量的推断问题可以看做是对后验概率的计算。因此提出了变分推断来计算后验分布。
变分推断核心思想主要包括两步：假设一个分布q(z;λ) 通过改变分布的参数λ，使q(z;λ) 靠近p(z∣x)。即用一个简单的分布q(z;λ) 拟合复杂的分布p(z∣x)。这种策略将计算p(z|x)的问题转化成优化问题：

收敛后，就可以用q(z;λ) 来代替p(z∣x)了。
  本文的目的是来求这个变分推理。下面涉及一些公式等价转换：
  
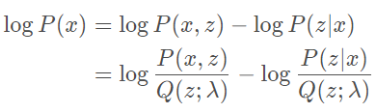
等式两边同时对Q(z)求期望，得：

到这里我们需要回顾一下我们的问题，从另一个角度再来思考一遍，寻找一个近似后验q∗(z)∈Q去近似p(z∣x)。

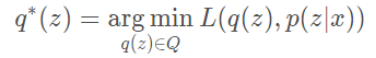
这里有两个注意点：1. 如何来选取这个Q。2. L表示它们之间的距离度量，通常用KL-divergence来表示：L(q(z),p(z∣x))=KL(q(z)∣∣p(z∣x))。用KL的原因在于它满足一些凸性，可导等性质。另一方面在于它具备一些性质：

p(z|x)p(z∣x)是我们的目标，q(z)是我们提出的需要去优化的分布。要去算这个优化的目标函数，我们需要已知p(z∣x)这个后验分布，但是我们不知道这个后验分布是什么。因此，上述这个公式我们是无法直接计算的。这就变成了一个循环的问题，为了要去算p(z∣x)，要去计算q(z)，而要计算q(z)又需要计算p(z∣x)。在没有其它约束的情况下，当q ∗=p(z∣x)的时候能够取到理论的最优值，但是p(z∣x)并不知道。
我们对KL Divergence最小化的问题做一些形式上的转变，期望去找到一个等价的问题：

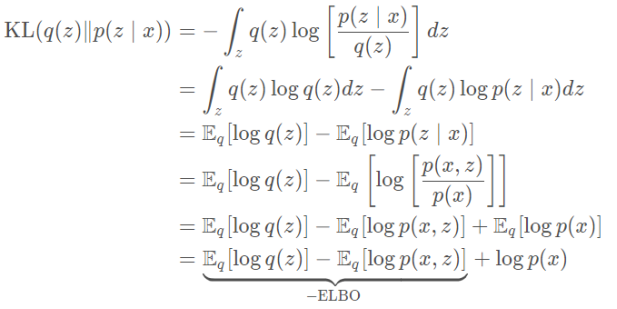
上述公式经过一定的变型之后，ELBO就是对数似然的一个下界函数：

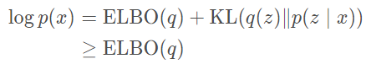
因为logp(x)是一个与q无关的常数，那么对KL(q(z)∥p(z∣x))的最小化问题就可以等价于最大化 ELBO(q)。而ELBO的表达式如下：

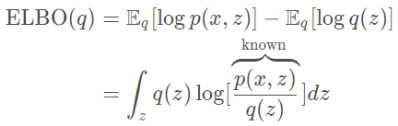
其中p(x,z)=p(x∣z)p(z)，是一个先验分布与似然的乘积。因此可以对ELBO做优化求解。现在，变分推断的目标变成：

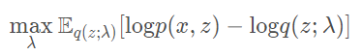
平均场变分族

实际问题中，我们可以选择什么形式的q(Z;λ)，一个简单而有效的变分族为平均场变分族。它假设了隐藏变量间是相互独立的：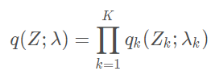
这个假设看起来似乎比较强，但实际应用范围还是比较广泛，我们可以将其延展为将有实际相互关联的隐藏变量分组，而化为各组联合分布的乘积形式即可。
  利用ELBO和平均场假设，我们就可以利用coordinate ascent variational inference（简称CAVI)方法来处理，利用条件概率分布的链式法则有 ：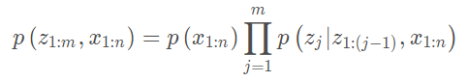
变分分布的期望为：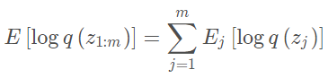
将其代入ELBO的定义得到：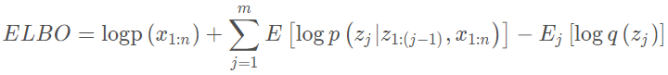
将其对zk求导并令导数为零有：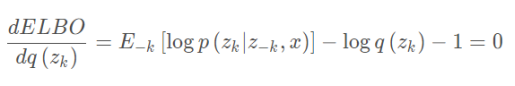
由此得到coordinate ascent 的更新法则为：
我们可以利用这一法则不断的固定其他的z的坐标来更新当前的坐标对应的z值，而CAVI算法中是不断的用如下形式更新：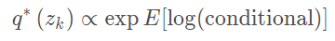
证明：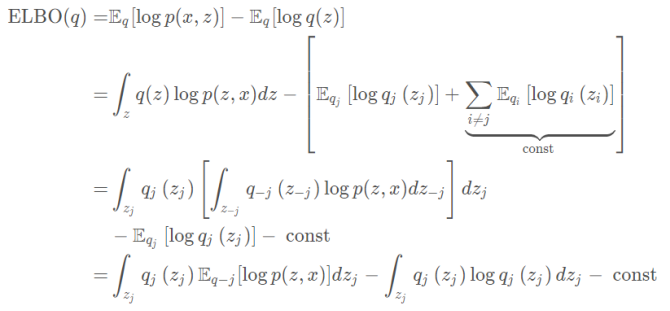
定义一个新的分布：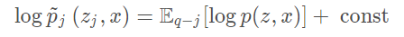
此时的ELBO就可以写成如下形式：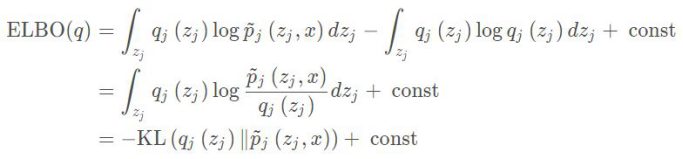
此时的KL divergence达到最小值时，当：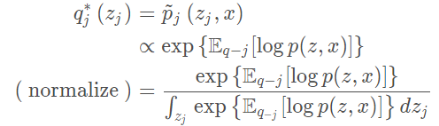
其完整算法如下所示：

黑盒变分推断

ELBO公式表达为：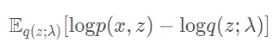
对用参数θ替代λ，并对其求导：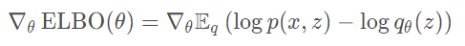
直接展开计算如下：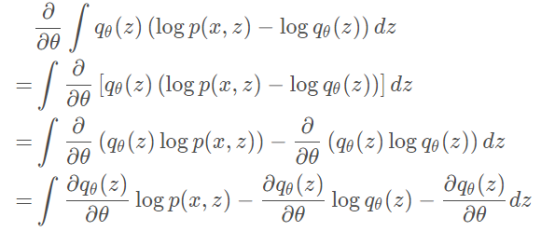
由于：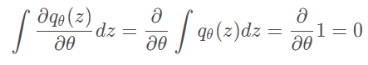
因此：
然后写成 SGD，就是所谓 Black Box Variational Inference (BBVI)。

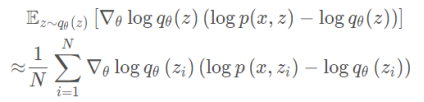
其中zi∼q θ (z)。其完整算法如下所示：

Discussion

本文简单介绍了变分推断的推导。变分推断在近似推断中是一个比较重要的思想，在变分自解码器等场景中广泛应用。相较于以 MCMC 方法为代表的马尔科夫方法，变分推断有着适应大规模数据计算的优势。通过查阅大量资料和学习视频，我基本理解了变分推断的大致思想和操作步骤。变分推断方法开辟了另一种思路，将后验推断问题巧妙地转化为优化问题进行求解，让我了解了一种处理问题的思路和方法，感受到贝叶斯学科的魅力。