Robotics:Aerial Robotics (空中机器人) (二)

Robotics:Aerial Robotics (空中机器人) (二)

week1.2 Energetics and System Design

该专栏为Coursera上宾夕法尼亚大学Kumar教授的课程——Robotics:Aerial Robotics的课程笔记和整理

原课程链接：https://www.coursera.org/learn/robotics-flight?specialization=robotics
知乎同文：https://zhuanlan.zhihu.com/p/482780836

Basic Mechanics (基本力学)

首先，我们来看四旋翼的基本力学原理。

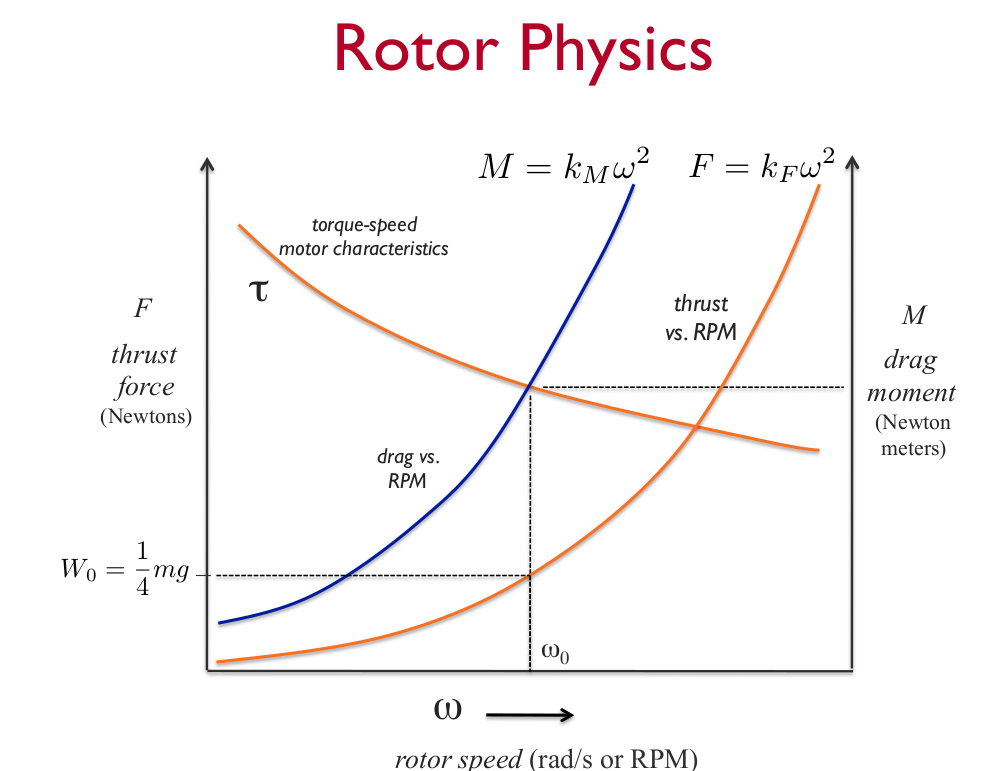
每个rotor（旋翼？）产生的推力（Thrust）与转速成二次关系（approximately quadratic），即
$$F=k_F{\omega }^2$$
rotor 旋转时，需要克服阻力矩（Drag moment），阻力矩与转速也近似成二次关系，即
$$M=k_M{\omega }^2$$
因此，对于四旋翼来说，当处于悬停状态时，每个rotor都需要克服$\frac{1}{4}$的重力。通过推力与转速的关系曲线，我们就可以确定产生这些力所需的转速${\omega }_0$。

当然，rotor要达到指定的转速，就需要克服阻力，这就需要引入motor了，根据motor的torque-speed 特性来选择合适的电机，以产生足够的扭矩来克服阻力矩。

综上，四旋翼悬停时，rotor通过转速补偿自身重力，根据重力即可确定rotor转速，这同时也给出了每个motor所需施加的扭矩大小。

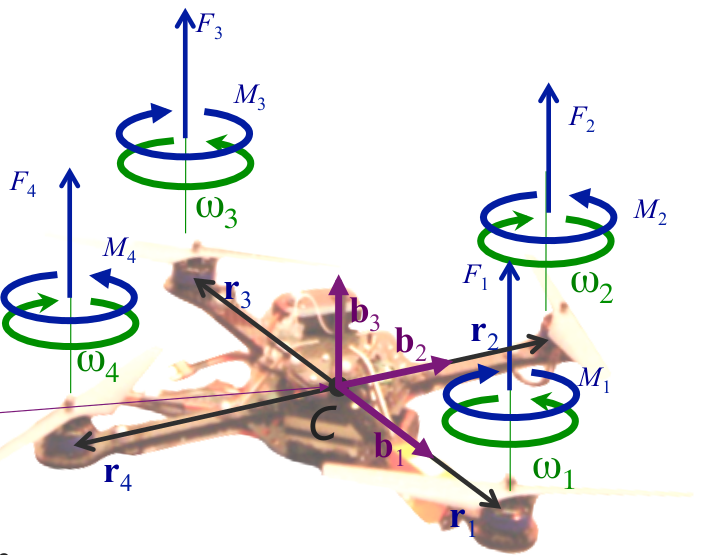
四旋翼的受力分析如图所示。合力为四个rotor的推力和自身的重力，合力矩为rotor施加的力矩和对应的阻力矩。
$$\begin{gathered} F_i=k_F{\omega }_i^2 \\ {M}_i=k_M{\omega }_i^2 \\ \text{Resultant Force:}\mathbf{F}={\mathbf{F}}_1+{\mathbf{F}}_2+{\mathbf{F}}_3+{\mathbf{F}}_4-mg{\mathbf{a}}_3 \\ \text{Resultant Moment:}\mathbf{M}={\mathbf{r}}_1\times {\mathbf{F}}_1+{\mathbf{r}}_2\times {\mathbf{F}}_2+{\mathbf{r}}_3\times {\mathbf{F}}_3+{\mathbf{r}}_4\times {\mathbf{F}}_4 \\ +{\mathbf{M}}_1+{\mathbf{M}}_2+{\mathbf{M}}_3+{\mathbf{M}}_4 \end{gathered}$$
当处于平衡状态时，合力和合力矩均为0。而当合力不为0时，就产生了加速度。因此，推力和重力决定了无人机的运动方式。

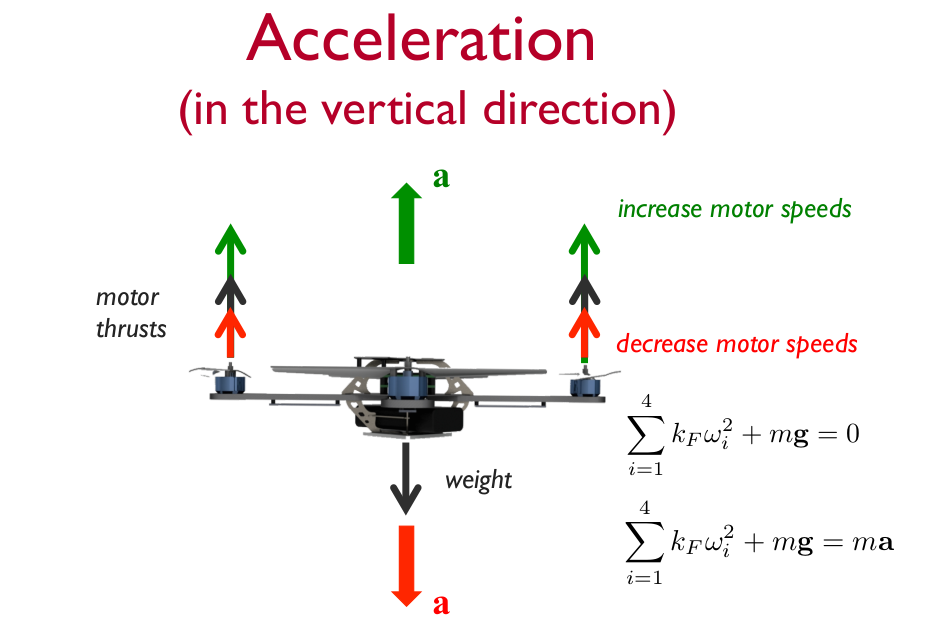
Dynamics and 1-D Linear Control (一维控制)

本节仅讨论一维方向——高度的控制。

首先考虑垂直方向的动力学方程：
$$\sum _{i=1}^4{k}_F{\omega }_i^2+m\mathbf{g}=m\mathbf{a}$$
我们选择加速度作为系统输入量 $u$，系统状态为 $x$，则
$$\text{ Input }u=\frac{1}{m}[\sum _{i=1}^4{k}_F{\omega }_i^{}$$