Feature-Steered Graph Convolutions for 3D Shape Analysis（FeaStConv）

最新推荐文章于 2024-06-22 09:35:10 发布

杰克船长有烦恼

最新推荐文章于 2024-06-22 09:35:10 发布

阅读量549

点赞数 2

分类专栏： GNN 模型文章标签： 3d 计算机视觉深度学习

本文链接：https://blog.csdn.net/m0_50976935/article/details/126363674

版权

GNN 模型专栏收录该内容

16 篇文章

订阅专栏

Feature-Steered Graph Convolutions for 3D Shape Analysis（FeaStConv）

摘要

卷积神经网络(CNNs)极大地影响了二维图像的视觉识别，现在在最先进的方法中无处不在。然而，CNNs不容易扩展到传统的局部卷积算子不能直接应用的非规则网格的数据，如3D形状网格或其他图形结构数据。为了解决这个问题，我们提出了一种新的图卷积算子来建立具有任意连通性的滤波器权值和图邻域之间的对应关系。我们方法的关键创新之处在于，这些对应关系是由网络学习到的特征动态计算出来的，而不是像之前的工作那样依赖于预定义的静态坐标。我们获得了优秀的实验结果，显著改善了以往的状态的形状对应结果。这表明我们的方法可以从原始输入坐标学习有效的形状表示，而不依赖于形状描述符。

1.引言

近年来，深度学习极大地提高了计算机视觉、语音识别和自然语言处理[13]等多个研究领域的水平。特别是，卷积神经网络(CNNs)现在已经成为视觉识别问题的计算解决方案，如图像分类[8]，语义分割[34]，目标检测[21]和图像字幕[32]。cnn还扩展了2D视觉信息之外的内容，并很容易推广到其他以规则矩形网格形式出现的数据。例如，音频信号[18]的一维卷积和视频信号[28]的三维空间和时间卷积已经证明了这一点。

在二维图像理解之外，特别有趣的是三维形状模型，可以考虑两种主要的表示类别。外在或欧拉表示是基于形状外部的参数化，最常见的是体素网格。这样的表示使标准的cnn能够应用于3D网格，但即使是最基本的形状转换也缺乏不变性。对形状进行简单的刚性转换可以导致3D网格表示的显著变化。此外，离散空间而不是形状往往是低效的，特别是对于移动和变形的对象，其中空间网格的很大一部分可能是空的，导致形状分辨率较差的表示[7]，或需要特殊的数据结构来处理稀疏的输入和/或输出[22,26]。另一方面，固有的或拉格朗日表示，如3D网格或体积量化，对许多形状转换是鲁棒的，并更有效地描述三维实体的离散与形状，而不是周围的空间。然而，cnn并不容易扩展到这种不规则结构的表示，在这种表示中，节点可以有不同数量的邻居。挑战在于在不规则的局部支持上定义类卷积算子，这些算子可以用作深度网络的层，用于预测任务，如三维网格上的形状对应，见图1

请添加图片描述

使用FeaStNet预测的形状对应(多尺度架构，无需细化)，从中立姿态的参考形状(左)转换纹理的三个例子

最近已经提出了许多超越常规网格数据组织的架构[2,4,5,9,11,12,14,15,20,25]。其中的一些技术可以推广到3D形状数据之外的其他领域，其中的数据可以组织成图形结构，包括例如社交网络或分子图[4,11]。然而，现有的方法有一些限制。光谱滤波方法[4,5,9,11]依赖于图拉普拉斯算子的特征分解。不幸的是，这种分解通常是不稳定的，使得跨不同形状泛化变得困难。另一方面，局部过滤方法[2,14,15]依赖于图上可能次优的硬编码局部伪坐标来定义过滤器。其他方法依赖于点云表示[12,20]，它不能利用网格中编码的表面信息，或者需要网格数据的特别转换来将其映射到单位球面[25]。

在本文中，我们提出了一种基于一种新的图卷积算子的深度神经网络FeaStNet，它不依赖于静态预定义的局部图伪坐标系，而是使用学习到的网络层的特征来动态确定滤波器权值和局部图邻域中节点之间的关联。在FAUST 3D形状对应基准上的优秀实验结果验证了我们的方法，并显著改善了最近最先进的方法。图1展示了使用我们的模型预测的对应关系进行纹理转换的几个例子。重要的是，这些结果是用原始的三维形状坐标作为输入，而不是传统的用于形状对应估计的三维形状描述符。他们证明，与现有的工程3D描述符相比，FeaStNet可以更好地学习局部形状属性。在点云上标记形状部分的附加结果与目前的技术水平相当，并说明我们的方法可以推广到没有明确表面信息的3D数据。

2. 相关工作

在本节中，我们简要回顾了图形卷积网络、处理3D形状的其他深度学习方法以及带有数据自适应过滤器的CNNs的相关工作。

Graph-convolutional networks

现有的将卷积网络推广到不规则图结构数据的方法可以分为两大类:光谱滤波方法和局部滤波方法。光谱方法建立在数学上优雅的方法上，使用图拉普拉斯算子的光谱特征分解来开发类卷积算子[4,5,9,11]。任何定义在图节点上的函数，例如特征，可以通过投影在拉普拉斯特征向量上映射到光谱域，其中滤波包括缩放特征基中的信号。虽然频谱技术在无噪声数据(如合成的3D形状模型)上取得了成功，但由于在不同的图上的全局分解是不稳定的，例如编码不同姿态的不同形状网格，因此频谱技术不太适合获得真实的形状。

为了更好地跨图进行泛化，许多技术遵循一种基于局部图过滤的策略[2,14,15,16,24]。这些方法的不同之处在于它们如何在局部图邻域中建立过滤器权重和节点之间的对应关系。Niepert等人。[16]依赖于节点的启发式排序，然后应用1D CNNs。Masci等人的geodesic CNN模型。[14]在网格上提取局部补丁，并与极坐标表达的滤波器进行卷积。采用角度最大池的方法处理滤波器的方向模糊，即在所有可能的方向上使用滤波器，并保留最大响应。Boscani等人。[2]提出了 anisotropic CNN模型，该模型利用各向异性斑块提取方法进一步扩展了geodesic CNN模型，利用最大曲率方向对斑块进行定向。Monti等人。[15]还使用每个节点周围固定的局部极坐标参数化图的局部补丁。他们通过估计将滤波器权重与局部伪坐标相关联的高斯均值和方差来学习滤波器形状。Simonovsky & Komodakis[24]使用边缘标签，它扮演着类似于局部伪坐标的角色，作为过滤器生成子网的输入。这个模型和我们的方法是类似的，我们不是依赖于手工设计的局部伪坐标，而是学习局部图块和滤波器权重之间的映射，使用之前的网络层的特征。

Deep networks for 3D shape data

除了光谱和局部滤波方法的图形，许多其他技术已被开发来处理三维形状数据的深度神经网络。Sinha等人。[25]使用球形参数化，在需要时填充网格中的孔，将形状映射到八面体上。这些八面体被切割并展开成方形图像，然后可以使用常规的CNNs进行处理。Wei等。[30]渲染形状的深度图，并用传统的CNNs处理它们，学习可以匹配的特征，建立形状对应关系。与这些将三维形状输入数据转换为二维图像并提供给传统CNNs的方法相反，我们提出了一种新的图卷积，可以直接处理不规则的图结构数据。

最近，提出了两种架构来处理点云数据。Klokov & lenmpitsky[12]在三维点云上提出了一个基于kd-tree的深度网络，基于分割的深度和方向共享整个树的参数。Qi等。[19, 20]将局部点处理层与最大池化层相结合来处理3D点云。通过构建，这些方法忽略了网格数据中可用的表面信息，并要求足够密集的采样，以避免由于空间上距离较远的点的接近而造成的假象。

Data-adaptive convolutional networks

传统CNN中的卷积层将上述特征映射的激活和学习到的滤波器权值相乘，并将结果相加，得到输出作为输入的线性函数，然后应用点向非线性。在空间变压器网络[10]和动态滤波网络[3]中，以上述特征映射为输入的子网用数据自适应变换代替标准的卷积层。在前者中，定位子网计算空间变换的参数，例如裁剪或调整大小，用于在卷积之前对前面的特征图进行空间重新采样。在后一种情况下，使用子网生成卷积滤波器，该滤波器将应用于上述特征映射。我们的方法在某种意义上是相关的，我们使用一个子网来关联图的一个局部“补丁”的元素到过滤器权重。

3. Graph convolutions using dynamic filters

在本节中，我们将简要回顾传统的CNNs，然后介绍我们的图卷积网络。

3.1 重构卷积CNN层

卷积CNN层将D个输入特征映射到E个输出特征映射。参数通常表示为一组 $D×E过滤器F_{d,e}$ ，每个大小为 $h \times w$ 像素, $d∈\{1，…， D\}， e∈\{1，…E\}$ 。卷积层中计算其中一个输出通道的计算可以描述为将每个D输入通道与相应的滤波器进行卷积，将D卷积结果求和，并添加一个恒定的偏差来计算输出特征图。

一个等价的但不太常见的表示，对于开发不规则图结构数据的扩展很有用。我们在 $M = h \times w$ 权重矩阵 $W_m∈R^{E×D}$ 的集合中重新排列卷积滤波器的权值。每个权重矩阵被用来将输入特征 $x∈R^D$ 投影到输出特征 $y∈R^E$ 。考虑到像素 $i$ 是它自己的一个邻居，将M个邻居的特征向量的投影与其相对位置对应的 $W_m$ 相加得到一个像素的卷积结果。参见图2中的说明。输出特征图中像素i的激活 $y_i∈R^E$ 为

请添加图片描述

其中 $b∈R^E$ 表示偏置项向量， $n (m, i)$ 其中像素 $i$ 表示第 $m$ 个相对位置的邻居的索引。例如，索引 $n (1, i) ， \dots ， n (9, i)$ 可以指以像素 $i$ 为中心的 $3 \times 3$ 块中的像素。

3.2 泛化到非规则输入域

对于规则输入的CNNs，例如像素网格，权重矩阵 $W_m∈R^{E×D}$ 和相对位置的邻居之间存在明确的一对一映射。其中 $m∈\{1，…， M\}$ 。卷积的中心像素。在不规则数据图的情况下，主要的挑战是定义邻居和权重矩阵之间的对应关系。我们建议以数据驱动的方式建立这种通信，使用在网络的前一层计算的特征上的函数，并学习该函数的参数作为网络的一部分。我们没有将节点 $i$ 的每个邻居 $j$ 分配给单个权矩阵，而是对所有 $M$ 个权矩阵的第 $j$ 个邻居使用软分配**(个人理解是动态的变化这些赋值)** $q_m(x_i, x_j)$ 。有了这些软赋值，我们将Eq.(1)一般化，并将特征从一层映射到下一层的函数定义为

请添加图片描述

其中 $q_m(x_i, x_j)$ 是 $x_j$ 对第 $m$ 个权矩阵的赋值， $N_i$ 是 $i$ (包括 $i$ )的邻居集合， $N_i|$ 是它的基数。我们使用局部特征向量线性变换上的软极大值来定义权值为

请添加图片描述

$∑^M_{M =1} q_m(x_i, x_j) =1$ , $u_m、v_m和c_m$ 为线性变换的参数。由于 $∑_{j∈N_i}\frac 1{|Ni|}∑^M_{M=1} q_m(x_i,x_j)=∑_{j∈N_i}\frac {1}{|N_i|}=1$ ，因此，无论节点的邻居数量如何，节点 $i$ 的**和(sum)**更新所涉及的权值为1。因此，我们的公式对节点程度的变化是稳健的。除了对eq.(3)中的特征进行单一的线性变换外，还可以采用更一般的变换，如多层子网络。如果 $_i|N_i| = M$ ，并且赋值是二进制的，即 $q_m(x_i,x_j)∈\{0,1\}$ ，基于邻居关于节点 $i$ 的相对位置。在图2中，我们演示了标准网格CNN和我们的图卷积网络中的计算。

请添加图片描述

左:一个标准CNN的插图，将参数表示为一组 $M = w \times h$ 权矩阵，每个权矩阵的大小为 $D \times e 。$ 每个权矩阵在输入patch(块)中与一个单一的相对位置相关联。右:我们的图卷积网络，其中输入patch(块)中的每个节点基于其特征，使用权值 $q_m(x_i,x_j)$ 以软方式与每个 $M$ 权值矩阵相关联。

在我们的实验中， $N_i$ 包含顶点 $i$ 和与 $i$ 通过边连接的所有顶点，即顶点周围的第一个环。然而，我们的方法允许使用更大的邻域，例如，环 $k \geq 2$ 或所有顶点达到一定的grodesic距离。这与传统CNNs中具有较大空间支持的滤波器类似。重要的是，与标准CNNs相比，上述公式将邻域大小 $N_i|$ 与权重矩阵M的数量解耦，从而将参数的数量解耦。因此，支持较大的过滤器不一定会增加参数的数量。我们的方法学习权重和邻居之间的映射，而不是依赖于膨胀[34]或权重共享的大型过滤器。

Translation invariant assignments in feature space

作为一种特殊情况，我们可以在式(3)中设置 $u_m =−v_m$ ，得到 $q^{ij}_m∝exp(u^⊤_m(x_j−x_i)+c_m)$ ，并导致特征空间中的权重平移不变性。这在输入特征包括空间坐标的应用程序中特别有意义，在这种情况下，对赋值函数施加平移不变性是很自然的。实验结果证实了使用原始空间三维坐标作为形状网格的输入特征时，平移不变性的积极作用。

Assignment by Mahalanobis distance in feature space

另一个有趣的情况发生在考虑Mahalanobis距离来确定分配权重 $q_m(x_i,x_j)$ 时。参考点 $z_m$ 与邻近特征 $x_{ij}=x_j−x_i$ 的居中版本之间的Mahalanobis距离，由一个正定矩阵Σ参数化，由

请添加图片描述

基于Mahalanobis距离的软分配符合公式(3)的形式， $c_m = z^⊤_mΣz_m, u_m =−2Σz_m, v_m =−u_m。$ 这些软赋值可以解释为在特征空间中对均值 $z_m$ 和共享协方差矩阵 $Σ^{−1}$ 的高斯混合模型的分量进行邻居的中心特征向量 $x_{ij}$ 的后验赋值。

这种对软分配的混合模型解释突出了我们的方法与Monti等人的方法之间的联系。[15]。在后者中，使用了一个类似的公式，其中中心 $z_m$ 与协方差矩阵 $Σ_m$ 一起学习。然而，这种混合是在先验定义的局部伪坐标 $x_{ij}$ 上定义的，例如网格上的局部极坐标，而不是在我们的公式中学习的特征。

使用该公式，我们还可以作为一种特殊情况，在像素网格上恢复传统的CNNs，将像素坐标作为特征向量x的一部分，使Mahalanobis距离仅依赖于这些坐标，并将中心 $z_m$ 精确地放置在相邻像素的相对位置上。将Mahalanobis距离乘以一个较大的常数将恢复Eq.(1)的标准CNN模型中使用的硬分配。

3.3 复杂性分析

权值矩阵 $W_m$ 是传统CNN和我们的方法所共有的，并且包含 $M D E$ 参数。在我们的方法中，传统CNN唯一的附加参数是向量 $u_m, v_m$ ，其中包含 $2 M D$ 参数。因此，参数的总数只增加一个因子 $(E + 2) / E = 1 + 2/ E$ ，忽略贡献很少参数的偏差项。

为了有效地评估激活量，我们首先将所有特征向量 $x_i$ 与权重矩阵 $W_m$ 、权重向量 $u_m和v_m$ 相乘。这需要 $O (NM D E)$ 操作，其中 $N$ 是图中的节点数。用 $k$ 表示每个顶点邻居的平均数量，我们就可以计算Eq.(3)中的权重和Eq.(2)中 $O (NM K E)$ 运算的激活量。因此，总计算代价为 $O (NME (K + D))$ 。

传统CNN中卷积层的代价为 $O (NME D)$ ，参考Eq.(1).因此，我们的方法的计算成本是可比较的，前提是邻居的数量K是可比较的或小于特征的数量d，这在实践中是典型的情况。

4. 实验

请添加图片描述

在一定距离内的测地线形状对应误差的分数。虚线显示的结果没有经过改进。

请添加图片描述

我们的模型的FAUST数据集和最近最先进的方法的对应准确性。

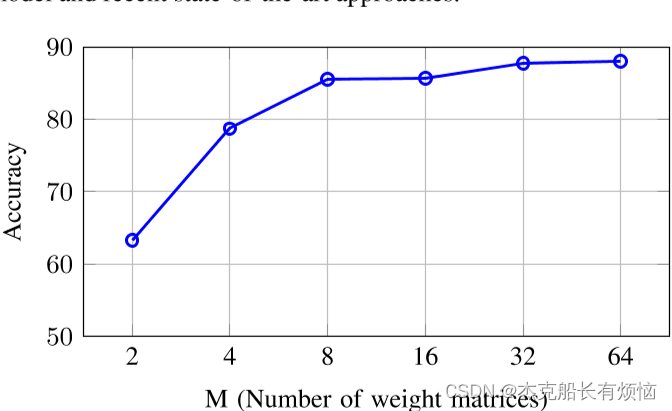
请添加图片描述

精度作为FAUST数据集的权重矩阵数量的函数，使用单一尺度架构。

5. 总结

我们提出了一种新颖的基于局部滤波的图卷积结构FeaStNet，它适用于一般的图结构，包括规则的和不规则的。主要的创新之处在于，我们的体系结构基于网络的前一层的特征动态地确定局部过滤器。因此，网络学习特征(i)有效地塑造局部滤波器，和(ii)为最终的预测任务提供信息。我们在FAUST数据集上获得了比最先进的3D网格对应技术显著提高的结果，并在ShapeNet数据集上获得了与最先进的部分标记技术相当的结果，我们在点云上的k近邻图上应用了我们的模型。在未来，我们计划扩展我们的架构来建模3D形状的其他属性，如外观或运动模式。

References

[1] F. Bogo, J. Romero, M. Loper, and M. Black. FAUST: Dataset and evaluation for 3D mesh registration. In CVPR, 2014.

[2] D. Boscaini, J. Masci, E. Rodola, and M. Bronstein. Learning shape correspondence with anisotropic convolutional neural networks. In NIPS, 2016.

[3] B. D. Brabandere, X. Jia, T. Tuytelaars, and L. V. Gool. Dynamic filter networks. In NIPS, 2016.

[4] J. Bruna, W. Zaremba, A. Szlam, and Y. LeCun. Spectral networks and locally connected networks on graphs. In ICLR, 2014.

[5] M. Defferrard, X. Bresson, and P. Vandergheynst. Convolutional neural networks on graphs with fast localized spectral filtering. In NIPS, 2016.

[6] I. Dhillon, Y. Guan, and B. Kulis. Weighted graph cuts without eigenvectors: A multilevel approach. PAMI, 29(11), 2007.

[7] R. Girdhar, D. Fouhey, M. Rodriguez, and A. Gupta. Learning a predictable and generative vector representation for objects. In ECCV, 2016.

[8] K. He, X. Zhang, S. Ren, and J. Sun. Identity mappings in deep residual networks. In ECCV, 2016.

[9] M. Henaff, J. Bruna, and Y. LeCun. Deep convolutional networks on graph-structured data. arXiv preprint arXiv:1506.05163, 2015.

[10] M. Jaderberg, K. Simonyan, A. Zisserman, and K. Kavukcuoglu. Spatial transformer networks. InNIPS, 2015.

[11] T. Kipf and M. Welling. Semi-supervised classification with graph convolutional networks. In ICLR, 2017.

[12] R. Klokov and V. Lempitsky. Escape from cells: Deep kdnetworks for the recognition of 3D point cloud models. InICCV, 2017.

[13] Y. LeCun, Y. Bengio, and G. Hinton. Deep learning. Nature, 52:436–444, 2015.

[14] J. Masci, D. Boscaini, M. Bronstein, and P. Vandergheynst. Geodesic convolutional neural networks on Riemannian manifolds. In ICCV Workshops, 2015.

[15] F. Monti, D. Boscaini, J. Masci, E. Rodol`a, J. Svoboda, and M. Bronstein. Geometric deep learning on graphs and manifolds using mixture model CNNs. In CVPR, 2017.

[16] M. Niepert, M. Ahmed, and K. Kutzkov. Learning convolutional neural networks for graphs. In ICML, 2016.

[17] M. Ovsjanikov, M. Ben-Chen, J. Solomon, A. Butscher, and L. Guibas. Functional maps: A flexible representation of maps between shapes. ACM Trans. Graph., 31(4), 2012.

[18] D. Palaz, M. Magimai-Doss, and R. Collobert. Analysis of CNN-based speech recognition system using raw speech as input. In InterSpeech, 2015.

[19] C. Qi, H. Su, K. Mo, and L. Guibas. Pointnet: Deep learning on point sets for 3D classification and segmentation. InCVPR, 2017.

[20] C. Qi, L. Yi, H. Su, and L. Guibas. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. InNIPS, 2017.

[21] S. Ren, K. He, R. Girshick, and J. Sun. Faster R-CNN: towards real-time object detection with region proposal networks. In NIPS, 2015.

[22] G. Riegler, A. Ulusoy, and A. Geiger. Octnet: Learning deep 3d representations at high resolutions. In CVPR, 2017.

[23] O. Ronneberger, P. Fischer, and T. Brox. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention, 2015.

[24] M. Simonovsky. Dynamic edge-conditioned filters in convolutional neural networks on graphs. In CVPR, 2017.

[25] A. Sinha, J. Bai, and K. Ramani. Deep learning 3D shape surfaces using geometry images. In ECCV, 2016.

[26] M. Tatarchenko, A. Dosovitskiy, and T. Brox. Octree generating networks: Efficient convolutional architectures for high-resolution 3D outputs. In ICCV, 2017.

[27] F. Tombari, S. Salti, and L. D. Stefano. Unique signatures of histograms for local surface description. In ECCV, 2010.

[28] D. Tran, L. Bourdev, R. Fergus, L. Torresani, and M. Paluri. Learning spatiotemporal features with 3D convolutional networks. In ICCV, 2015.

[29] M. Vestner, R. Litman, E. Rodola, A. Bronstein, and D. Cremers. Product manifold filter: Non-rigid shape correspondence via kernel density estimation in the product space.arXiv preprint arXiv:1701.00669, 2017.

[30] L. Wei, Q. Huang, D. Ceylan, E. Vouga, and H. Li. Dense human body correspondence using convolutional networks. In CVPR, 2016.

[31] Z. Wu, R. Shou, Y. Wang, and X. Liu. Interactive shape cosegmentation via label propagation. Computers & Graphics, 38:248–254, 2014.

[32] K. Xu, J. Ba, R. Kiros, K. Cho, A. Courville, R. Salakhutdinov, R. Zemel, and Y. Bengio. Show, attend and tell: Neural image caption generation with visual attention. In ICML, 2015.

[33] L. Yi, V. Kim, D. Ceylan, I.-C. Shen, M. Yan, H. Su, C. Lu, Q. Huang, A. Sheffer, and L. Guibas. A scalable active framework for region annotation in 3D shape collections. InSIGGRAPH Asia, 2016.

. Ceylan, I.-C. Shen, M. Yan, H. Su, C. Lu, Q. Huang, A. Sheffer, and L. Guibas. A scalable active framework for region annotation in 3D shape collections. InSIGGRAPH Asia, 2016.

[34] F. Yu and V. Koltun. Multi-scale context aggregation by dilated convolutions. In ICLR, 2016.