旋转，旋转矩阵和欧拉角（内旋、外旋）

最近学习过程中看到欧拉角的外旋等价于内旋的相反顺序，对此自己有些困惑，无法理解，所以查阅了一些资料，并添加自己的一些理解，整理为如下内容。大家阅读过程中如果发现了错误，欢迎指正。

1. 旋转坐标变换

在进行叙述之前，首先梳理一遍旋转坐标变换。 对于旋转，可以分为两类，对向量的旋转和对坐标系的旋转（坐标系由三个轴的向量组成，本质也是对向量的旋转）。（对于旋转，向量和坐标相似，以下不做区分）

1.1. 对向量的旋转

这是最常见的和容易理解的，我们一般都会认为坐标系是固定不动的，而旋转作用于物体上。即在旋转之后，坐标系的位置是固定不变的，而向量的方向发生改变，即向量坐标改变。
$${\mathbf{t}}_1=f(\mathbf{t})$$
这里我们使用抽象的函数表达式$f(x)$表示旋转操作，$f(x)$可以是旋转矩阵、四元数等。对于向量$\mathbf{t}$，如果是3维空间（默认为3维），则为$(a,b,c{)}^T$，这里$a,b,c$分别是向量在三个坐标轴$(\mathbf{u},\mathbf{v},\mathbf{w})$的分量。

1.2. 对坐标系的旋转

除了对向量的旋转，另一种是对坐标系的旋转。这一种在机器人学中是很常见的。由于机器人中存在非常多的坐标系，需要描述不同坐标系之间的旋转关系。

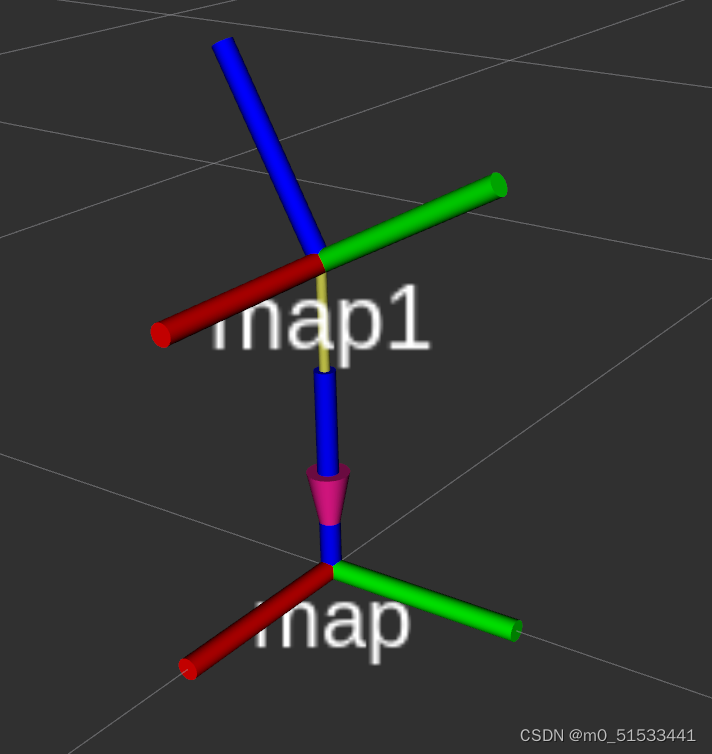
下面我们以上图的两个坐标系进行说明（这里忽略坐标系之间的位置平移，仅考虑旋转）。上图中，map1坐标系由map坐标系旋转得到，计算由map到map1的旋转变换。由于坐标系是有三个向量表示，也就是三个坐标轴方向的向量由map变换到map1坐标系的方向。假设map坐标系中x, y, z三个坐标轴的向量为$(\mathbf{u},\mathbf{v},\mathbf{w})$，旋转后$({\mathbf{u}}_1,{\mathbf{v}}_1,{\mathbf{w}}_1)$，则
$${\mathbf{u}}_1,{\mathbf{v}}_1,{\mathbf{w}}_1=f(\mathbf{u},\mathbf{v},\mathbf{w})$$
令$\mathbf{A}=(\mathbf{u},\mathbf{v},\mathbf{w})$， ${\mathbf{A}}_1=({\mathbf{u}}_1,{\mathbf{v}}_1,{\mathbf{w}}_1)$，则上式变为：
$${\mathbf{A}}_1=f(\mathbf{A})$$

1.3. 两种旋转方式的等价性

上述两种旋转方式，本质上是等价的。对于向量的旋转，假设坐标系是固定不动的。由于运动是相对的，这种旋转也可以等价为向量不动，而坐标系发生了反方向的旋转。其旋转的结果都是向量相对于坐标系的方向产生变化，且变化结果相同，即在旋转之后，这两种方式的向量在坐标系的表示是相等的。

初始图

旋转向量

旋转坐标系

如果是对向量进行旋转，向量旋转之前的坐标为$\mathbf{t}$，旋转之后的坐标为${\mathbf{t}}_1=f(\mathbf{t})$。
如果是对坐标系进行旋转，坐标系旋转之前，向量的坐标为$\mathbf{t}$。坐标系旋转之后，虽然从全局的位置看，向量的方向没有改变，但是坐标系$\mathbf{A}$方向发生了改变，变为了${\mathbf{A}}_1$，此时向量在新的坐标系中的表达式将改变。所以${\mathbf{A}}_1{\mathbf{t}}_1=\mathbf{At}$，即${\mathbf{t}}_1={\mathbf{A}}_1^{-1}\mathbf{At}$。
下面将通过旋转矩阵说明两种方式得到的${\mathbf{t}}_1$是相等的。

2. 旋转矩阵

下面使用旋转矩阵和具体的解析表达式对上述进行解释和说明。

首先是使用旋转矩阵对向量的旋转。对于向量$\mathbf{b}$，开始位置在${\mathbf{b}}_1$，围绕Z轴逆时针旋转$\theta$度得到${\mathbf{b}}_2$，则这个旋转矩阵可以表示为：
$$\mathbf{R}=\left[\begin{array}{ccc}cos(\theta )& -sin(\theta )& 0\\ sin(\theta )& cos(\theta )& 0\\ 0& 0& 1\end{array}\right]$$

下面是使用旋转矩阵对坐标系的旋转。首先，假设空间中存在一个全局坐标系$\mathbf{T}$，存在一个向量$\mathbf{b}$。另外，存在两个坐标系${\mathbf{T}}_1=({\mathbf{u}}_1,{\mathbf{v}}_1,{\mathbf{w}}_1)$和${\mathbf{T}}_2=({\mathbf{u}}_2,{\mathbf{v}}_2,{\mathbf{w}}_2)$，向量在两个坐标系的表达式分别为${\mathbf{b}}_1$和${\mathbf{b}}_2$。其中${\mathbf{T}}_1$和${\mathbf{T}}_2$的坐标轴向量的具体表达式都是在全局坐标系$\mathbf{T}$下表示的。
对于同一个向量$\mathbf{b}$，在不同的坐标系下的完整表达式都应该是相等的，且都等于在全局坐标系$\mathbf{T}$下的表达式，即${\mathbf{T}}_1{\mathbf{b}}_1={\mathbf{T}}_2{\mathbf{b}}_2=\mathbf{b}$。所以${\mathbf{b}}_1={\mathbf{T}}_1^{-1}{\mathbf{T}}_2{\mathbf{b}}_2$。令$\mathbf{R}={\mathbf{T}}_1^{-1}{\mathbf{T}}_2$，即旋转矩阵。则上式变为${\mathbf{b}}_1=\mathbf{R}{\mathbf{b}}_2$，等价于将坐标系从${\mathbf{T}}_2$旋转到${\mathbf{T}}_1$后，向量的坐标变化。
这里使用了三个坐标系，全局坐标系$\mathbf{T}$，两个局部坐标系${\mathbf{T}}_1$和${\mathbf{T}}_2$。对于全局坐标系$\mathbf{T}=(\mathbf{u},\mathbf{v},\mathbf{w})$，其基底一般为单位矩阵。对于坐标系${\mathbf{T}}_1$和${\mathbf{T}}_2$，其基底是坐标系向量轴在全局坐标系下的表示，是标准正交基，但一般不是单位矩阵。
根据上面对坐标系关系的表述，全局坐标系不一定需要显式指定，可以假定坐标系${\mathbf{T}}_1$与全局坐标系$\mathbf{T}$重合。此时，坐标系${\mathbf{T}}_1$的基底是单位矩阵，而${\mathbf{T}}_2$的基底是坐标轴向量在坐标系${\mathbf{T}}_1$下的表示。回到旋转矩阵$\mathbf{R}={\mathbf{T}}_1^{-1}{\mathbf{T}}_2$，此时${\mathbf{T}}_1$是单位矩阵，即$\mathbf{R}={\mathbf{T}}_2$，这里${\mathbf{T}}_2$就是前面说的，${\mathbf{T}}_2$的基底是坐标轴向量在坐标系${\mathbf{T}}_1$下的表示。
下面我们通过绕Z轴的旋转举例说明。假定坐标系${\mathbf{T}}_2$绕Z轴顺时针旋转$\theta$度得到坐标系${\mathbf{T}}_1$，则${\mathbf{T}}_2$在${\mathbf{T}}_1$下的表达式为：
$${\mathbf{T}}_2=\left[\begin{array}{ccc}cos(\theta )& -sin(\theta )& 0\\ sin(\theta )& cos(\theta )& 0\\ 0& 0& 1\end{array}\right]$$
由于$\mathbf{R}={\mathbf{T}}_2$，即上述的旋转矩阵$\mathbf{R}$表示将坐标系${\mathbf{T}}_2$旋转到${\mathbf{T}}_1$。

从上面的推导可以看到，$\mathbf{R}=\left[\begin{array}{ccc}cos(\theta )& -sin(\theta )& 0\\ sin(\theta )& cos(\theta )& 0\\ 0& 0& 1\end{array}\right]$，既可以表示一个向量围绕Z轴逆时针旋转了$\theta$度，也可以表示坐标系围绕Z轴顺时针旋转了$\theta$度。下面通过图示的方式展示了两种旋转之间的等价性。

3. 欧拉角

在有了上面的基础上，接下来就可以了解欧拉角中让人困惑的内旋和外旋。
欧拉角是用来描述刚体或坐标系在一个固定坐标系中的姿态，通过使用三个坐标轴的旋转分量，来描述旋转。欧拉角根据旋转轴的不同，以及旋转顺序的不同，分为不同的类别。这里我们主要介绍内旋和外旋的区别。
介绍内旋和外旋之前，首先要说明两个坐标系，一个是全局坐标系，在旋转过程中是固定不变的，另一个是局部坐标系，是固定在刚体身上的。对刚体的旋转可以等价是对局部坐标系的旋转。总体来说，内旋和外旋是根据围绕坐标系的不同进行判断，内旋是围绕局部坐标系进行的，而外旋是围绕全局坐标系进行的。

3.1. 内旋

内旋就是围绕着局部坐标系进行的。这里以z-y-x的顺序，先后绕这三个轴的旋转角度为$\alpha ,\beta ,\gamma$。下图中，红色坐标轴为x方向，绿色为y方向，蓝色为z方向。

欧拉角的三次旋转，前后对应四个刚体的局部坐标系，我们分别假设坐标系为${\mathbf{T}}_0,{\mathbf{T}}_1,{\mathbf{T}}_2,{\mathbf{T}}_3$。下面使用旋转矩阵描述这些旋转过程。

1. ${\mathbf{T}}_0\to {\mathbf{T}}_1$ ，围绕${\mathbf{T}}_0$的Z轴旋转$\alpha$度
   注意目标是计算旋转之后刚体在全局坐标系的位姿，而刚体在局部坐标系的位姿是保持不变的，只是不同时刻局部坐标系位姿不同。假设刚体上的一个点在局部坐标系的坐标为$p$。刚体开始的初始局部坐标系${\mathbf{T}}_0$，我们假定与固定的全局世界坐标系$\mathbf{T}$重合。
   当旋转到${\mathbf{T}}_1$时，刚体上的点在${\mathbf{T}}_0$坐标系的坐标为$p_0^1={\mathbf{R}}_{01}{p}_1^1$，这里$p_0^1$中的1表示刚体位于${\mathbf{T}}_1$位置，0表示点在${\mathbf{T}}_0$的坐标，$p_1^1$的值等于$p$。根据旋转矩阵中介绍的坐标系的旋转，${\mathbf{R}}_{01}$等于${\mathbf{T}}_1$坐标轴向量在${\mathbf{T}}_0$坐标系下的表示，所以${\mathbf{R}}_{01}$的表达式如下：
   $${\mathbf{R}}_{01}=\left[\begin{array}{ccc}cos(\alpha )& -sin(\alpha )& 0\\ sin(\alpha )& cos(\alpha )& 0\\ 0& 0& 1\end{array}\right]$$

2. ${\mathbf{T}}_1\to {\mathbf{T}}_2$ ，围绕${\mathbf{T}}_1$的Y轴旋转$\beta$度
   和上面${\mathbf{T}}_0\to {\mathbf{T}}_1$的过程类似。当刚体旋转到${\mathbf{T}}_2$时，刚体上的点在${\mathbf{T}}_1$坐标系的坐标为$p_1^2={\mathbf{R}}_{12}{p}_2^2$，这里$p_1^2$中的2表示刚体位于${\mathbf{T}}_2$位置，1表示点在${\mathbf{T}}_1$的坐标，$p_2^2$的值等于$p$。${\mathbf{R}}_{12}$等于${\mathbf{T}}_2$坐标轴向量在${\mathbf{T}}_1$坐标系下的表示。所以${\mathbf{R}}_{12}$的表达式如下：
   $${\mathbf{R}}_{12}=\left[\begin{array}{ccc}cos(\beta )& 0& sin(\beta )\\ 0& 1& 0\\ -sin(\beta )& 0& cos(\beta )\end{array}\right]$$

3. ${\mathbf{T}}_2\to {\mathbf{T}}_3$ ，围绕${\mathbf{T}}_2$的X轴旋转$\gamma$度
   同理和上面过程类似。当刚体旋转到${\mathbf{T}}_3$时，刚体上的点在${\mathbf{T}}_2$坐标系的坐标为$p_2^3={\mathbf{R}}_{23}{p}_3^3$，这里$p_2^3$中的3表示刚体位于${\mathbf{T}}_3$位置，2表示点在${\mathbf{T}}_2$的坐标，$p_3^3$的值等于$p$。${\mathbf{R}}_{23}$等于${\mathbf{T}}_3$坐标轴向量在${\mathbf{T}}_2$坐标系下的表示。所以${\mathbf{R}}_{23}$的表达式如下：
   $${\mathbf{R}}_{23}=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos(\gamma )& -sin(\gamma )\\ 0& sin(\gamma )& cos(\gamma )\end{array}\right]$$

在有了上面每一步旋转前后的坐标变换，则最终可以得到${\mathbf{T}}_0$旋转到${\mathbf{T}}_3$时，刚体上的点在${\mathbf{T}}_0$坐标系下的表示：
$$p_0^3={\mathbf{R}}_{03}{p}_3^3={\mathbf{R}}_{01}{p}_1^3={\mathbf{R}}_{01}{\mathbf{R}}_{12}{p}_2^3={\mathbf{R}}_{01}{\mathbf{R}}_{12}{\mathbf{R}}_{23}{p}_3^3$$
即：
$${\mathbf{R}}_{03}={\mathbf{R}}_{01}{\mathbf{R}}_{12}{\mathbf{R}}_{23}$$
在一般的文章介绍中，绕Z轴的旋转矩阵${\mathbf{R}}_{01}$用${\mathbf{R}}_z(\alpha )$表示，绕Y轴的旋转矩阵${\mathbf{R}}_{12}$用${\mathbf{R}}_y(\beta )$表示，绕X轴的旋转矩阵${\mathbf{R}}_{23}$用${\mathbf{R}}_x(\gamma )$表示，所以${\mathbf{R}}_{03}={\mathbf{R}}_z(\alpha ){\mathbf{R}}_y(\beta ){\mathbf{R}}_x(\gamma )$

3.2. 外旋

外旋与内旋相对，是围绕着固定的全局坐标系进行的，与局部坐标系无关，因此可以看做是对向量的旋转。这里同样以z-y-x的顺序，先后绕这三个轴的旋转角度为$\alpha ,\beta ,\gamma$，不过这里是全局坐标系。 同样假设开始时，刚体上的一个点在全局坐标系（与局部坐标系重合）的坐标为$p$

1. 绕z轴旋转$\alpha$
   根据之前讲解的，刚体中一点从$p_0$绕z轴旋转$\alpha$度到$p_1$位置，$p_1={\mathbf{R}}_z(\alpha )p_0$，其中${\mathbf{R}}_z(\alpha )$为：
   $$R_z(\alpha )=\left[\begin{array}{ccc}cos(\alpha )& -sin(\alpha )& 0\\ sin(\alpha )& cos(\alpha )& 0\\ 0& 0& 1\end{array}\right]$$

2. 绕y轴旋转$\beta$
   上面得到的$p_1$位置还是在全局坐标系下，所以绕y轴旋转$\beta$度得到$p_2$位置，$p_2={\mathbf{R}}_y(\beta )p_1$，其中${\mathbf{R}}_y(\beta )$为：
   $${\mathbf{R}}_y(\beta )=\left[\begin{array}{ccc}cos(\beta )& 0& sin(\beta )\\ 0& 1& 0\\ -sin(\beta )& 0& cos(\beta )\end{array}\right]$$

3. 绕x轴旋转$\gamma$
   $p_2$的位置还是在全局坐标系下，所以绕z轴旋转$\gamma$度得到$p_3$位置，$p_3={\mathbf{R}}_x(\gamma )p_2$，其中${\mathbf{R}}_x(\gamma )$为：
   $${\mathbf{R}}_x(\gamma )=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos(\gamma )& -sin(\gamma )\\ 0& sin(\gamma )& cos(\gamma )\end{array}\right]$$

所以刚体中一点$p_0$经过z-y-x顺序的外旋，得到的位置为：$p_3={\mathbf{R}}_x(\gamma )p_2={\mathbf{R}}_x(\gamma ){\mathbf{R}}_y(\beta )p_1={\mathbf{R}}_x(\gamma ){\mathbf{R}}_y(\beta ){\mathbf{R}}_z(\alpha )p_0$，即$\mathbf{R}={\mathbf{R}}_x(\gamma ){\mathbf{R}}_y(\alpha ){\mathbf{R}}_z(\alpha )$。

根据上面的推导，围绕z-y-x顺序的内旋，得到的旋转矩阵为：${\mathbf{R}}_z(\alpha ){\mathbf{R}}_y(\beta ){\mathbf{R}}_x(\gamma )$，而围绕z-y-x顺序的外旋，得到的旋转矩阵为：${\mathbf{R}}_x(\gamma ){\mathbf{R}}_y(\beta ){\mathbf{R}}_z(\alpha )$。所以相同的旋转顺序和角度的欧拉角，内旋和外旋的旋转矩阵顺序相反。

3.3. 其它

1. 对于内旋，可以从旋转向量的角度去解释吗？

理论上可以的。围绕z-y-x顺序的旋转，旋转矩阵的顺序也是${\mathbf{R}}_x(\gamma ){\mathbf{R}}_y(\beta ){\mathbf{R}}_z(\alpha )$。由于绕z轴旋转时，局部坐标系和全局坐标系是重合的，$R_z(\alpha )==\left[\begin{array}{ccc}cos(\alpha )& -sin(\alpha )& 0\\ sin(\alpha )& cos(\alpha )& 0\\ 0& 0& 1\end{array}\right]$。旋转之后，局部坐标系和全局坐标系不重合，${\mathbf{R}}_x(\gamma )$和${\mathbf{R}}_y(\beta )$的具体表达式需要根据旋转方向在全局坐标系的具体位置进行计算，表达式将比较复杂。

2. 同理，对于外旋，可以通过旋转坐标系进行解释吗？

一样可以的，同样除了开始时，局部坐标系和全局坐标系重合，$R_z(\alpha )==\left[\begin{array}{ccc}cos(\alpha )& -sin(\alpha )& 0\\ sin(\alpha )& cos(\alpha )& 0\\ 0& 0& 1\end{array}\right]$，之后的${\mathbf{R}}_y(\beta )$和${\mathbf{R}}_x(\gamma )$的表达式将比较复杂。

参考

1. 欧拉角细节/旋转顺序/内旋外旋
2. 欧拉角内旋和外旋的等价性
3. 两种欧拉角及其到旋转矩阵的转化
4. 欧拉角和旋转矩阵之间的转换