【雷达通信一体化】OQAM-OFDM雷达-通信联合系统的波形设计【附MATLAB代码】

文献来源：微信公众号 EW Frontier

链接：【雷达通信一体化】OQAM-OFDM雷达-通信联合系统的波形设计【附MATLAB代码】【雷达通信一体化】OQAM-OFDM雷达-通信联合系统的波形设计【附MATLAB代码】https://mp.weixin.qq.com/s?__biz=Mzk0NTQzNDQyMw==&mid=2247489875&idx=1&sn=8128dd1d7dabac46450f0e20e261206f&chksm=c314230bf463aa1d24395cb54d9842be0aa9976defbe2025f0ffabf6db164526d8f9be76692a&token=106157288&lang=zh_CN#rd

Abstract

在本文中，我们开发了一种基于偏移正交幅度调制的正交频分复用（OQAM-OFDM）的联合雷达通信系统，它能够同时实现雷达和通信功能。本文首先介绍了一种考虑多径效应的雷达和通信系统的统一接收信号模型。提出了一种同时实现信息解调和雷达脉冲压缩的方法。通过对雷达工作和通信的信噪比（SNR）分别进行分析，通过设计OQAM-OFDM的发送序列，求解了最大化雷达信噪比和通信信噪比的优化模型。由于优化问题是NP-难的，我们提出了一种联合方法，包括循环算法和交替方向法的乘子算法（CA-ADMM）获得的解决方案。最后，数值结果验证了所提出的方案的上级性能。

关键字：雷达通信系统，基于偏置正交幅度调制的正交频分复用（OQAM-OFDM），信息解调，脉冲压缩，信噪比（SNR），循环算法和交替方向乘法器算法（CA-ADMM）。

1.介绍

在过去的几十年里，雷达和通信一直是分开发展的，有着不同的目标。雷达主要用于探测和跟踪目标[1，2]，而通信系统主要用于信息传输[3-7]。随着电子技术的进步，一种既利用雷达又利用通信的装置已经开发了几种应用，例如智能交通系统[8]，它需要感知环境并传递信息。因此，联合雷达通信（RadCom）系统可以享受减少系统重量、尺寸、功耗等的优点，并且近年来获得了很多兴趣[9]。

到目前为止，对RadCom系统的研究分为两类：非同时系统和同时系统[10]。对于非同时系统，雷达和通信功能在不同的时隙中操作[11]。虽然它很容易实现，但在通信过程中存在雷达检测盲区，也影响了通信性能。相反，同时系统采用共享信号，即，RadCom信号，它既能实现目标探测又能实现信息传输功能.目前，存在三种用于设计RadCom信号的方法。首先，雷达和通信信号独立产生，然后叠加[12，13]。第二，通信数据被调制在雷达信号上[14，15]。第三，通信信号被设计为例如多载波信号[16，17]。这种方法被认为是最有前途的一种，因为它能够在雷达检测和信息传输方面提供高性能[17]。

特别地，正交频分复用（OFDM）波形已经被许多研究用作RadCom信号[17-19]。在文献[18]中，作者分析了基于OFDM信号的RadCom系统的可行性。文[19]中的工作实现了距离探测、合成孔径雷达（SAR）成像和通信功能。此外，在[17，20-22]中提出了用于RadCom系统的基于循环前缀（CP）的传统OFDM方案，其对于雷达检测实现了良好的旁瓣性能并且克服了多径效应。然而，CP的存在降低了频谱效率，也浪费了大量的能量。此外，众所周知，OFDM信号可能在频域中遭受大的旁瓣，这潜在地导致高载波间干扰（ICI）和带外辐射[23，24]。

最近，已经研究了不需要CP的基于偏移正交幅度调制的OFDM（OQAM-OFDM）作为OFDM的替代方案[24-27]。通常，将具有良好频率局部化特性的原型滤波器[28]应用于OQAM-OFDM信号以呈现低得多的频谱旁瓣[26]。基于此，OQAM-OFDM波形已经在多个雷达系统中被考虑。在[29-31]中导出了OQAM-OFDM信号的平均模糊函数，有完美的图钉形状在[32]中，提出了一种基于M序列的OQAM-OFDM信号，以改善信号相关性和雷达距离分辨率。此外，在[34]中检查了使用具有低旁瓣的OQAM-OFDM信号的近似范围间小区干扰（IRCI）的无脉冲压缩方法。然而，所有上述研究仅将OQAM-OFDM信号应用于雷达应用，而没有考虑通信功能。

在本文中，我们提出了一个系统，同时执行雷达和通信功能的OQAM-OFDM信号。本文的主要贡献概括如下：

1)提出了一种基于OQAM-OFDM的RadCom信号。传统的OQAMOFDM信号利用发射序列来携带信息，这导致RadCom系统的性能不佳。为了提高性能，我们在OQAM-OFDM信号中引入相位项来传输信息。然后，可以设计每个子载波上的发射序列，以满足雷达和通信的要求。

2)提出了一种统一的RadCom系统接收信号模型。将雷达的每个距离单元视为通信路径，接收信号模型可以构造为发射信号和信道响应的卷积。

3)针对雷达和通信的不同目标，提出了不同的解决方法，并分别分析了信噪比（SNR）性能。然后，通过设计OQAM-OFDM信号的发送序列，提出了一种结合循环算法和交替方向乘法算法（CA-ADMM）的方法，以最大化雷达信噪比和通信信噪比。

最后，数值模拟结果提供了评估所提出的计划的有效性。仿真结果表明，我们提出的CA-ADMM算法可以提高雷达信噪比和通信误码率（BER）。此外，我们提出的方案提供了上级性能优于传统的方法。

对于本文的其余部分，我们首先在第2节中推导系统模型。然后，在第3节中提出了通信解调。第4节中提供了雷达脉冲压缩。然后，在第5节中设计了联合RadCom OQAM-OFDM波形。数值模拟结果在第6节中给出。最后，在第7节中得出了本文的结论。

2.系统模型

图1所示为RadCom系统，它可以支持雷达和通信功能。通过发射RadCom信号，我们可以通过处理RadCom站接收到的回波来检测目标。同时，通信用户接收RadCom信号，并对发送的信息进行解调。在本文中，我们介绍了一种RadCom信号的基础上，OQAM-OFDM信号。传统上，在通信系统中利用OQAM-OFDM信号的每个子载波上的序列来承载信息。相比之下，在我们提出的RadCom系统中，我们另外在OQAM-OFDM信号中引入相位项来携带信息。然后，我们可以设计每个子载波上的序列，以优化雷达和通信性能，这将在后面讨论。

考虑具有K个子载波、2 M个OFDM符号和长度Ls的OQAM-OFDM信号。将在第k个子载波上发送的真实的序列表示为dk，在第i时隙（i = 0，1，...，Ls − 1）可以写成

图1 RadCom系统示意图

其中，h（i）表示对称实值原型滤波器[28]，并且φk，m可以写为

其中θk，m ∈（m ∈ = 0，1，...，M-1）  是利用相移键控（PSK）调制发送的信息。因此，偶数和奇数符号分别传输ejθk，m  的真实的和虚部。因此，我们将传输的复杂信息定义为

对于通信接收机，假设信道冲激响应bcom r  已知，长度为Lcom v  的接收信号v com i  可以建模为[33]

其中Rcom  是bcom r  的长度，ωcom i  表示接收器处具有零均值和方差σ2 com  的加性白色高斯噪声。类似地，对于雷达，给定发射信号si，RadCom站的接收信号vrad i  表示为[34]

其中Rrad  表示距离单元的数量，布拉德r表示第r个距离单元内散射体的响应，ωrad i  是雷达处具有零均值和方差σ2 rad  的加性白色高斯噪声，Lrad ν  表示接收信号的长度。

注意，对于通信系统，接收机对（4）中的信号进行解调以估计ck，m  。同时，对于雷达系统，为了实现目标检测，需要进行脉冲压缩以提高信噪比，这相当于从（5）中的接收信号中检测出布拉德r  。为此，本文根据雷达和通信系统的不同目标，分别对通信解调和雷达脉冲压缩进行了研究。

3.用于通信系统的解调

在本节中，我们导出从（4）中的接收信号获取发送信息的方法。首先，我们将（4）中的接收信号解调为

假设原型滤波器Lh  的长度远长于信道的最大延迟扩展Rcom  ，即，Lh Rcom  .因此，原型滤波器函数在延迟扩展内基本保持不变[36]。

然后，将ωk，m  表示为解调噪声，（6）可以重写为[33，34]

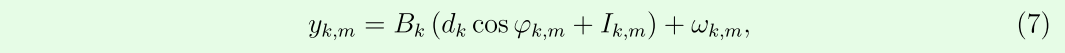
其中，Bk  对应于信道的频率响应  ，

Ik，m  表示干扰，

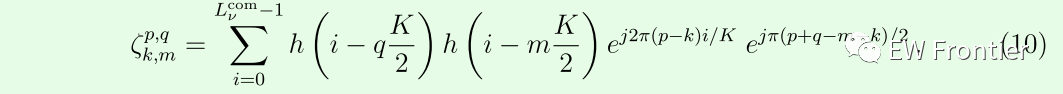
这里，Ik，m\zeta_{k,m}^{p,q}  是p，q ∈ Θp，q  的虚值[34]，因此Ik，m  也是虚值。

最后，我们可以得到[35]。

然后，我们可以重建

  从（12），我们可以解调发送的信息。此外，为了分析解调性能，我们计算每个子载波的输出SNR为

其中，每个子载波的噪声方差是  值得注意的是，每个子载波的通信输出SNR与发送序列dk  和信道频率响应Bk  相关。因此，我们可以设计dk以改善SNRcom k  ，这将在后面讨论。

4.雷达脉冲压缩

在本节中，我们提出了一种简单而有效的雷达脉冲压缩方法。根据（5），我们将雷达接收信号以矢量表示法重写为：

其中，v = v0 v1 · · · vLrad ν −1 <$T ∈ CLrad ν  是接收信号向量，S ∈ CLrad ν ×Rrad  表示发送信号矩阵，其由下式给出：

B = [b 0 b1 · · · bRrad−1]T ∈ CRrad  表示与距离单元对应的矢量，w =<$ω0 ω1 · · · ωLrad ν −1 <$T ∈ CLrad ν  表示噪声矢量。

从（15）式中，S  的列是线性无关的。因此，SHS\mathbf{S}^H\mathbf{S}  是可逆的。

此外，在实际应用中，Lrad ν > Rrad  是显而易见的。然后，通过估计b  可以容易地实现脉冲压缩，如[37]

这里，噪声协方差矩阵变为  

这样，脉冲压缩被完美地实现，并且对于每个距离单元的估计不存在来自其它距离单元的干扰。

类似地，我们还推导出第r个距离单元的雷达输出SNR为：

为了实现最大SNRrad r\mathrm{SNR}_{r}^{r\mathrm{ad}}，可以证明SHS  应该是对角的[37]。然而，通常，SHS  可以不是对角矩阵。此外，根据（15），很明显，SHS  的对角元素与SHS  的对角元素相同  ，其中s = [s 0 s1 · · · sLs-1]T  是发送信号矢量。此外，从（1），s可以表示为s = Φd  ，其中Φ\mathbf{\Phi}  是Ls ×K  矩阵，其第（i，k）  个元素给定为

并且d = [d 0 d1 · · · dK-1]T  表示OQAM-OFDM信号的发送序列。因此，为了最大化雷达信噪比，我们可以设计d  ，使S\mathbf{S}  满足条件SHS = SHS <$2I  。

5.RadCom联合优化

基于前面对RadCom信号的推导，我们发现雷达信噪比和通信信噪比都依赖于d  。在本节中，我们开发了一个优化模型，以在最小通信SNR约束下最大化雷达SNR，可以写为

其中约束（19 b）表示发送信号的能量约束，并且SNRmin表示获得可接受BER的通信最小输出SNR。因此，通过解决问题（19），我们不仅最大化了雷达SNR性能，而且还保证了通信SNR性能。

从（19）式中，不容易直接获得d  的最优解。因此，我们提出了一个CA-ADMM算法来解决问题（19）。请注意，（19）的目标是S的四次函数，这很难处理。因此，在[38，39]中采用类似的方法，我们将（19）的目标替换为

其中Q  是Lrad ν ×Rrad  半酉矩阵。然后，我们可以通过使用CA算法[38]来解决问题（20）。

让我们表示

作为SH\mathbf{S}^H的奇异值分解（SVD），其中U ∈ CRrad×Rrad  是酉矩阵，V ∈ CRrad ×Rrad  表示对角矩阵，V ∈ CLrad v ×Rrad  表示半酉矩阵.然后，对于给定的S，（20）的解可以给出为：

因此，基于（15），问题（20）可以转换为

其中qr ∈ CLs×1  是<$Q  的第r列的子向量，其位置与  S的第r列中s  的位置相同。因此，最终的优化模型用于优化  可被构造为

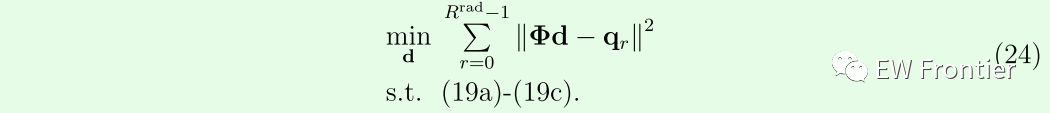
由于约束的非凸性，问题（24）通常是NP难问题[40，41]。因此，我们引入ADMM算法[42]以获  得（24）的解。首先，我们将增广拉格朗日量发展为

其中λ 是长度为Ls的乘子向量，αα表示惩罚因子。然后，可以利用ADMM算法以交替方式确定（s，d，λ）  ，以通过考虑问题（24）中的约束来最小化L（s，d，λ）  。

让我们分别将s（t）、d（t）、λ（t）、q（t）r  表示为s、d、λ、qr  的第t次迭代值。q（t+1）r  可以由式（22）用s（t）  确定。此外，我们可以通过以下方式更新s，d，λ  ：

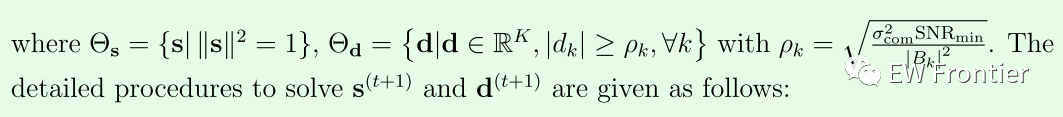
  ,  ,求解s（t+1）  和d（t+1）  的详细过程如下：

5.1.给定d（t），λ（t），q（t+1）r  的s  的更新

忽略常数项，关于s  的子问题可以写为：

可以简化为

其中x = λ（t）− αHΦd（t）  。然后，我们可以得到一个封闭形式的解决方案，

5.2.给定s（t+1），λ（t），q（t+1）  的d  的更新

包含依赖于  d的项的子问题由下式给出：

  那么，（31）中的问题可以表示为：

问题（32）可以通过坐标下降（CD）算法解决[43，44]。为了更新dk  ，我们保持d  的其他元素不变，

其中a1  、a2  和a3  被定义为a1 = [k]k，k，  

因此，我们可以得到dk  的解为：

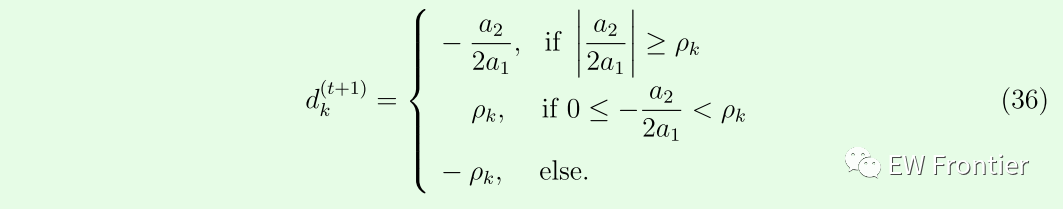
我们继续上述过程，直到d（t）  的所有元素都被更新。然后，我们最终获得d（t+1）  。

在算法1中总结了针对问题（19）提出的CA-ADMM算法，其中主要计算复杂度与距离单元的数量Rrad  和迭代次数有关。对于每次迭代，主要计算复杂度对应于更新qr  时的SVD。因此，所提出的CA-ADMM算法需要O（F（Rrad）3）O(F(R^{\mathrm{rad}})^3)  的计算复杂度，其中F表示迭代次数。

6.数值结果

本节旨在评估所提出的基于CA-ADMM的RadCom设计方法。我们将子载波的数量设置为K = 128 ，将符号的数量设置为2 M = 4 ，将范围单元的数量设置为Rrad = 64 ，并且将信道长度设置为Rcom = 6 ，其中功率分布（以dB为单位）{-6.0，0.0，-7.0，-22.0，-16.0，-20.0} 和相应的延迟分布（以µs为单位）{-3，0，2，4，7，11} 。我们使用二进制相移键控（BPSK）调制方案。利用升余弦滤波器作为OQAM-OFDM信号的原型滤波器。d和λ随机初始化。所有模拟结果均为通过100个实验的Monte Carlo实验获得。

图2 具有不同α值的迭代的残差κ

在算法1中，惩罚因子α和所需的最小通信输出SNRmin 影响所提出的方法的性能。为了验证这种效果，图2显示了残差κ（t）= max s（t）−Φd（t），d（t）− d（t−1） 与不同α SNR min = −30 dB ，输入SNR 0 dB ）的迭代关系。这里，对于CA-ADMM算法，收敛阈值被设置为10 - 4 [42，45]。从图2中可以看出，当α较小时，例如α = 10，100， 所提出的算法不能保证收敛。如果α较大，则可以确保收敛。因此，应选择较大的α。在图3中，输入SNR为0 dB且SNRmin = −30 dB时，我们给出了雷达输出SNR和积分旁瓣比（ISLR）随迭代次数的变化曲线。可以看出，雷达输出SNR随着迭代而逐渐增长，并且最终收敛到SNRmax，这是可达到的最大SNR。SNRmax被计算为发送信号的长度。此外，随着迭代次数的增加，ISLR减小并快速收敛。该算法实现了4.35 dB的增益为输出SNR和3.73 dB的ISLR相比，没有迭代的情况下。同时，我们可以发现，较小的α实现快速收敛。此外，在输入SNR为10 dB且SNRmin = −30 dB的情况下，通过蒙特卡罗实验获得的通信BER曲线如图4所示。类似地，我们可以看到BER性能随着迭代而改善。因此，我们可以得出结论，首先需要为α选择一个合适的值，以确保收敛，使算法尽快收敛。我们设α = 500以下模拟。此外，从这些曲线图中，我们确认，雷达和通信的性能都得到了改善。

图4 不同α值迭代的通信误码率曲线

接下来，我们分析SNRmin带来的影响。在图5中描绘了在不同的SNR最小值和0 dB的输入SNR的情况下关于迭代的残差κ。正如预期的那样，我们可以检查所提出的算法随着迭代而逐渐收敛，当SNRmin不大于输入SNR时。对于较大的SNRmin值，收敛所需的时间较少，但是当SNRmin太大时，算法不能收敛。原因是较大的SNRmin意味着较强的通信约束，导致减少可行集的大小。

图5不同SNRmin值下迭代的残差κ

图6雷达SNR相对于具有不同SNRmin值的迭代

在图6和图7中，分别展示了具有不同SNR最小值的雷达和通信仿真结果。雷达的输入信噪比为0 dB，通信的输入信噪比为10 dB。从图6中可以看出，SNRmin 对雷达性能的影响很小，所有结果都很快收敛到SNRmax 。在图7中，更大的SNRmin 导致更好的BER性能。为此，在选取最小信噪比时，可以使其等于输入信噪比，这样不仅可以最大化雷达输出信噪比，而且可以大大提高通信性能。

在图8和图9中，我们进一步分析了在将SNRmin设置为输入SNR的情况下，不同输入SNR的雷达和通信性能。给出具有随机生成的d的结果作为比较的基准。在图8中，所提出的算法总是可以达到最大SNR，并且输出SNR和ISLR性能都优于传统方案。与传统方案相比，该算法的输出信噪比增益为4.43 dB，ISLR增益为2.99 dB。图9示出了通信BER仿真结果。随着输入信噪比的增加，该算法实现了较大的性能增益相比，传统的方案。从以上仿真结果中，我们验证了所提出的方案的有效性。与传统方法相比，该方案具有上级的雷达和通信性能。

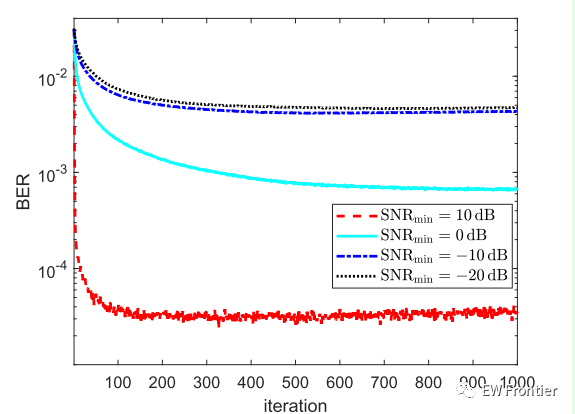
图7 不同SNR最小值迭代的通信误码率

图8 相对于输入SNR的雷达仿真结果。(a)输出SNR（b）ISLR

图9 相对于输入SNR的通信BER结果

7.结论

本文提出了一种RadCom OQAM-OFDM联合系统，它同时实现了通信和雷达脉冲压缩。建立了雷达和通信系统统一的接收信号模型。为了满足雷达和通信的需要，我们提出了不同的方法来解决这个问题。分析了OQAMOFDM信号的输出信噪比，发现OQAMOFDM信号的发射序列与雷达信噪比和通信信噪比有关。通过对发射序列的设计，建立了在保证最小通信信噪比的前提下，最大化雷达信噪比的优化模型。我们采用CA算法将问题转化为一个二次问题，然后在ADMM算法的框架下求解。最后，通过数值仿真结果验证了该方案的有效性。该方案与传统方案相比，具有上级雷达信噪比、旁瓣性能和误码性能。

​部分MATLAB代码

function [iterations, Zplot, SNRplot, SNRmaxplot, SNReqplot, ERRORplot, ERRORplot2, SS] = cyclic ()

% Parameters
K = 128;                        % # of subcarriers
Rcom = 6;                       % channel length
Rrad = 64;                      % # of range cells
SNRin = 10;                     % input SNR = 10dB
sigma = sqrt(1)/sqrt(K);        % std.

% Communication Channel
hdB = zeros(K, 1);
hdB(1:Rcom, 1) = [-6.0 0.0 -7.0 -22.0 -16.0 -20.0];    % power profile
h = zeros(K, 1);
h(1:Rcom, 1) = 10.^(hdB(1:Rcom, 1)/10);
H = fft(h);                                            % frequency response

% Threshold
SNRmin = 10.^(-20/10);                      % threshold SNR : -20dB per each subcarrier
rho = sigma * sqrt(SNRmin) ./ abs(H);       % threshold power of each subcarrier rho = [rho(0) rho(1) ... rho(K-1)]

% Initialization
d = randn(K, 1) .* ((2 .* randi([0 1], K, 1) - 1) + 1i * (2 .* randi([0 1], K, 1) - 1));
d = sqrt(SNRin) * d / norm(d);                % OFDM freq domain d = [d(0) d(1) ... d(K-1)]

dd = zeros(K, 1);
for idx = 1 : K
    dd(idx) = (2 .* randi([0 1], 1, 1) - 1) + 1i .* (2 .* randi([0 1], 1, 1) - 1);
    dd(idx) = dd(idx) / norm(dd(idx));
end
dd = sqrt(SNRin) * dd / norm(dd);

ss = K * ifft(dd);
S_S = zeros(K, Rrad);
for idx = 1 : Rrad
    S_S(:,idx) = circshift(flipud(ss), K-Rrad+idx);
end

Rand = orth(randn(K, K));
Q = sqrt(K)* sqrt(SNRin) * Rand(:, 1:Rrad);            % semiunitary matrix
s = K * ifft(d);                                       % OFDM time domain s = [s(0) s(1) ... s(K-1)]
S = zeros(K, Rrad);
for idx = 1 : Rrad
    S(:,idx) = circshift(flipud(s), K-Rrad+idx);
end

% Objective Function
y = norm(S'*S - (Q'* Q), 'fro');

jdx = 0;
z = y;

iterations = zeros(0, 0);
Zplot = zeros(0, 0);
SNRplot = zeros(0, 0);
SNRmaxplot = zeros(0, 0);
SNReqplot = zeros(0, 0);
ERRORplot = zeros(0, 0);
ERRORplot2 = zeros(0, 0);

while true
    y = z;
    % #1 : Obtain S given Q
    S = alg1 (SNRin, K, Rrad, rho, Q, d);
    
    % #2 : Obtain Q given S
    [U, ~, V] = svd(S');
    Vtilde = V(:, 1:Rrad);
    Q = sqrt(K) * sqrt(SNRin) * Vtilde * U';
    
    z = norm(S'*S - (Q'*Q), 'fro');
    
    SS = S' * S;
    
    SNRrad = sum(1 ./ diag(inv(S'*S))) / Rrad;
    SNRraddB = 10 * log(SNRrad) / log(10);
    
    s = S(:,Rrad);
    d = (1/K) * fft(flipud(s));
    
    SNRmax = 1 / norm(s).^(-2);
    SNRmaxdB = 10 * log(SNRmax) / log(10);

    SNReq = sum(1 ./ diag(inv(S_S' * S_S))) / Rrad;
    SNReqdB = 10 * log(SNReq) / log(10);
    
    
    SNRcom = abs(d).^2 .* abs(H).^2 / sigma^2;
    ErrorP = sum(erfc(SNRcom ./ sqrt(2))) ./ K;
    
    SNRcom2 = abs(dd).^2 .* abs(H).^2 / sigma^2;
    ErrorP2 = sum(erfc(SNRcom2 ./ sqrt(2))) ./ K;
    
    jdx = jdx + 1;
    iterations = horzcat(iterations, jdx);
    Zplot = horzcat(Zplot, z);
    SNRplot = horzcat(SNRplot, SNRraddB);
    SNRmaxplot = horzcat(SNRmaxplot, SNRmaxdB);
    SNReqplot = horzcat(SNReqplot, SNReqdB);
    ERRORplot = horzcat(ERRORplot, ErrorP);
    ERRORplot2 = horzcat(ERRORplot2, ErrorP2);
    
    if abs(z-y) < 1e-5      % stopping criterion
        break
    end
    
end

end