(SOGI-PLL)基于simulink与DSP联合开发

1.SOGI-PLL简介

​​SOGI-PLL（Second-Order Generalized Integrator-Based Phase-Locked Loop）​​ 是一种结合二阶广义积分器（SOGI）与锁相环（PLL）的先进同步控制技术，专为复杂电网环境下高精度提取基波相位与频率信息而设计。其核心在于通过SOGI结构构建正交信号生成器（Quadrature Signal Generator, QSG），结合自适应频率反馈机制，提升PLL在谐波干扰、电压跌落及频率波动等非理想工况下的动态性能与抗扰能力。

小林同学

2.Simulink中的DSP底层配置（以28069M为例）

在设置里选择硬件实现为DSP28069M。

采用EPWM中断运行算法（15khz）

EPWM配置如下：

采用中心对齐模式 

死区设置为2us

使能EPWM触发ADC采集

 配置一个GPIO进入中断时翻转一次电平（验证算法执行时间）

到此步底层配置完成。

3.SOGI-PLL算法模型搭建 

整体模型如下所示，输入为电网电压通过SOGI输出α和β分量，通过坐标变换后对Q轴分量进行锁相控制。

SOGI 采用matlab-function输出。

function [alhfa, beta] = sogi_shift(ua, t,w0)
    % 定义持久变量，确保 alhfa 和 beta 跨函数调用保持其值
    persistent alhfa_persistent beta_persistent
    
    if isempty(alhfa_persistent)
        alhfa_persistent = single(0);  % 初始值为0
        beta_persistent = single(0);   % 初始值为0
    end

    % 定义常数 k 和 w0
    k = single(1);          % k = 1


    % 计算 x = ua - alhfa
    x = single(ua) - alhfa_persistent;

    % 更新 alpha (alhfa)
    alhfa_persistent = alhfa_persistent + (x * k - beta_persistent) * w0 * t;
    
    % 更新 beta
    beta_persistent = beta_persistent + alhfa_persistent * w0 * t;
    
    % 输出更新后的 alhfa 和 beta
    alhfa = alhfa_persistent;
    beta = beta_persistent;
end

采用三次谐波注入的方法得到所需的CCR值

到此步算法模型搭建完成。 

4.硬件实验

连接驱动电路和LCL滤波器。

调不好的PI参数（TI官方有参数整定的详细文档）

不使能锁相环时，电网电压和逆变器输出电压按各自的角度运行。

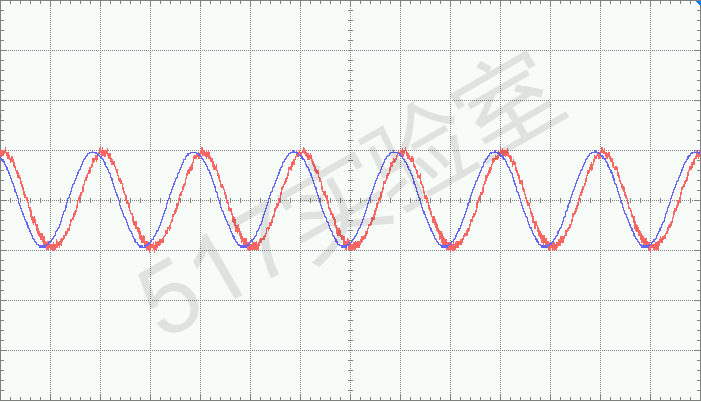
使能锁相后，电压电压和逆变器输出电压同频同相位。

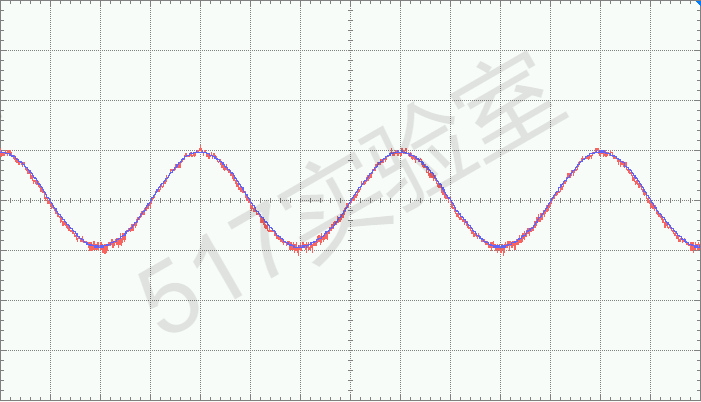
至此，锁相环模型验证完成。