【分子材料发现】——EGNN：E(n) Equivariant Graph Neural Networks（论文简述）

E(n) Equivariant Graph Neural Networks

论文地址：https://arxiv.org/abs/2102.09844

0 Abstract

这篇论文介绍了一种新的模型，用于学习对旋转、平移、反射和排列具有等变性的图神经网络，称为E(n)-等变图神经网络（EGNN）。与现有方法相比，我们的工作不需要在中间层使用计算成本高昂的高阶表示，同时仍然能够达到竞争性或更好的性能。此外，与现有方法仅限于三维空间的等变性不同，我们的模型可以轻松扩展到更高维度的空间。我们通过动态系统建模、图自编码器中的表示学习以及预测分子属性来展示我们方法的有效性。

1 Introduction

1.1 Equivariance（等变性）

对于抽象群$g\in \mathcal{G}$，$T_g:X\to X$是抽象群在$X$上的一组变换。如果在$g$的输出空间上存在一个等效变换$S_g:Y\to Y$，那么我们称函数$\varphi :X\to Y$对$g$具有等变性。（即：先平移/旋转/排列再映射，和先映射再平移/旋转/排列效果是一样的。）：
$\varphi (T_g(X))=S_g(\varphi (x))(1)$

1.2 Graph Neural Networks（图神经网络）

图神经网络是作用于图结构数据的排列等变网络。对于给定的图$\mathcal{G}=(\mathcal{V},\mathcal{E})$，节点$v_i\in \mathcal{V}$，边$e_{ij}\in \mathcal{E}$。定义一个图卷积层为：

其中$h_i^l\in R^{nf}$是第$l$层中节点$v_i$的$nf$维嵌入。$a_{ij}$是边的属性。$N(i)$表示节点$v_i$的邻居集合。最后，$\varphi (e)$和$\varphi (h)$分别是边和节点操作，它们通常由多层感知器逼近。

1.3 E(3)

许多问题表现出3D平移和旋转对称性。一些例子包括点云、3D分子结构或N体粒子模拟。对应这些对称性的群被称为欧几里得群：SE(3)，或者当包括反射时称为E(3)。通常希望对这些任务的预测要么对E(3)变换是等变的，要么是不变的。

2 Method

2.1 method

对于图$\mathcal{G}=(\mathcal{V},\mathcal{E})$，节点$v_i\in \mathcal{V}$，边$e_{ij}\in \mathcal{E}$。在1.2中GNN的基础上，除了节点嵌入$h_i\in R^{nf}$之外，EGNN还考虑与每个图节点相关联的$n$维坐标$x_i\in R^n$。EGNN在$x_i$上保持旋转和平移不变性，并且它也以与GNN相同的方式保持节点$\mathcal{V}$上排列的不变性。

EGNN使用的等变图卷积层（Equivariant Graph Neural Networks, EGCL）以：节点嵌入 h l = { h 0 l , . . . , h M − 1 l } h^l = \{h^l_0,...,h^l_{M-1}\} hl={h0l​,...,hM−1l​}，坐标嵌入 x l = { x 0 l , . . . , x M − 1 l } x^l = \{x^l_0,...,x^l_{M-1}\} xl={x0l​,...,xM−1l​}和边信息$\mathcal{E}=(e_{ij})$作为输入，$h^{l+1}$ 和 $x^{l+1}$作为输出。即$h^{l+1},x^{l+1}=EGCL[h^l,x^l,\mathcal{E}]$。定义这一层的方程如下：

EGCL与GNN不同的主要存在于式子(3)和(4)，在(3)中加入了两个坐标之间的相对距离的平方${\Vert x_i^l-x_j^l\Vert }^2$。(4)是保留等变性的关键，$x_i$的更新是由所有相对差$(x_i-x_j{)}_{\forall j}$的加权和来更新的，其权重由函数${\varphi }_x:R^{nf}\to R^1$的输出提供，该函数以前一次边操作的边嵌入$m_{ij}$作为输入并输出一个标量值；其中$C=\frac{1}{M-1}$。

2.2 Analysis on E(n) equivariance

EGNN对任何平移向量$g\in R^n$在$x$上具有平移等变性，并且对于任何正交矩阵$Q\in R^{n\times n}$具有旋转和映射等变性。即满足：
$Q{x}^{l+1}+g,h^{l+1}=EGCL(Q{x}^l+g,h^l)$

$h_l$是E(n)不变的特征，以此推断：
1.由方程3知$m_{ij}$是E(n)不变的：因为它除了依赖于$h_l$之外，还依赖于平方距离${\Vert x_i^l-x_j^l\Vert }^2$，这些都是E(n)不变的。
2.由方程4知$x_i^{l+1}$是E(n)不变的：通过加权和的差异$(x_i-x_j)$计算$x_i^{l+1}$，是type-1向量变换，是E(n)不变的。
3.方程5和6知$h^{l+1}$是E(n)不变的，因为它们只依赖于$h_l$和$m_{ij}$，这两项都是E(n)不变的。
因此$h^{l+1}$是E(n)不变的，$x^{l+1}$对$x^l$是E(n)等变的。归纳得到EGCLs的组合是等变的。

2.3 Extending EGNNs for vector type representations

通过方程4替换为方程7能够跟踪粒子的动量：

扩展了EGCL层为$h^{l+1},x^{l+1},v^{l+1}=EGCL[h^l,x^l,v^{\text{init}},\mathcal{E}]$。将坐标更新（方程4）分解为两个步骤，首先计算速度$v_i^{l+1}$，然后使用速度更新位置$x_i^{l+1}$。初始速度$v^{\text{init}}$由${\varphi }_v:R^N\to R^1$缩放，该函数将节点嵌入$h_i^l$映射到一个标量值。如果初始速度设置为零，方程4和7将完全相同。

2.4 Inferring the edges

对于一组节点数据，也许并不总是提供其邻接矩阵，在这种情况下可以假设一个全连接图，其中所有节点$(i\ne j)$都像方程5相互交换消息。这种全连接方法不适用于大型点云，因此通过局部限制消息的交换$m_i={\sum }_{j\in N(i)}{m}_{ij}$到邻域$\mathcal{N}(i)$，以避免信息溢出。
EGNN提出了一个简单的解决方案来推断模型中的图关系/边。给定每个节点$i$的一组邻居$\mathcal{N}(i)$，将聚合操作（方程5）重写如下：

其中$e_{ij}$在节点$(i,j)$之间有边时取值为1，否则为0。因此可以使用函数近似关系$e_{ij}\approx {\varphi }_{inf}(m_{ij})$，其中${\varphi }_{inf}:R^{nf}\to [0,1{]}^1$是一个类似于线性层后接sigmoid的函数，它以当前边嵌入作为输入，输出对其边值的软估计。因为只对已经是E(n)不变的消息$m_{ij}$进行操作这种修改不会改变模型的E(n)属性。

3 Experiment

3.1 Modelling a dynamical system — N-body system

在动力学系统中，一个函数定义了几何空间中一个点或一组点的时间依赖性。在这个实验中，EGNN预测一组粒子的位置，这些粒子通过简单的交互规则建模，但可以表现出复杂的动态：将带电粒子N体实验扩展到三维空间，该系统由5个粒子组成，它们带有正电荷或负电荷，并在三维空间中有位置和速度。系统由物理规则控制：粒子根据它们的电荷相互吸引或排斥。这是一个等变任务，因为在输入粒子集上的旋转和平移不影响轨迹的变换。

3.1.1 Dataset

训练采样了3000条轨迹，验证2000条，测试2000条。每条轨迹持续1000个时间步。对于每条轨迹，提供了初始粒子位置 p ( 0 ) = { p 1 ( 0 ) , … , p 5 ( 0 ) } ∈ R 5 × 3 p^{(0)} = \{p^{(0)}_1, \ldots, p^{(0)}_5\} \in \mathbb{R}^{5 \times 3} p(0)={p1(0)​,…,p5(0)​}∈R5×3，它们的初始速度 v ( 0 ) = { v 1 ( 0 ) , … , v 5 ( 0 ) } ∈ R 5 × 3 v^{(0)} = \{v^{(0)}_1, \ldots, v^{(0)}_5\} \in \mathbb{R}^{5 \times 3} v(0)={v1(0)​,…,v5(0)​}∈R5×3以及它们各自的电荷 c = { c 1 , … , c 5 } ∈ { − 1 , 1 } 5 c = \{c_1, \ldots, c_5\} \in \{-1, 1\}^5 c={c1​,…,c5​}∈{−1,1}5。任务是在1000个时间步后估计这五个粒子的位置。优化估计位置与真实位置之间的平均均方误差。

3.1.2 Implementation details

实验使用了2.4中包含速度的模型扩展。我们将位置$p^{(0)}$作为模型的第一层坐标$x^0$输入，将速度$v^{(0)}$作为方程7中的初始速度，$v_i^{(0)}$的范数$\Vert v_i^0\Vert$也通过线性映射作为特征提供给$h_i^0$。电荷作为边属性$a_{ij}=c_i{c}_j$输入。模型输出最后一层坐标$x^L$作为估计位置。

3.1.3 Results

将EGNN与非等变GNN，以及等变GNN：Radial Field，Tensor Field Networks和SE(3) Transformer进行比较。如Table 2所示，EGNN在运行效率方面显著优于其他方法。它将错误率比表现第二好的方法降低了32%。

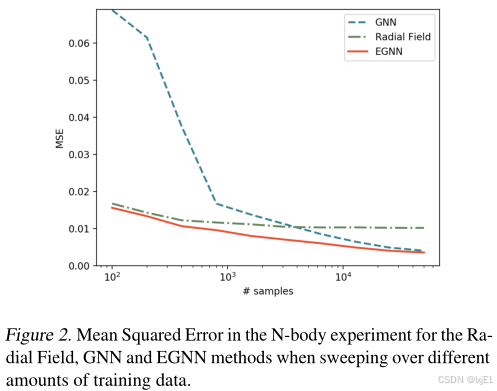
3.1.4 Analysis for different number of training samples

为分析EGNN在小数据和大数据环境下的性能，生成新的包含50000条样本的训练数据集。比较了EGNN、GNN及Radial Field的性能。结果如Figure 2所示。EGNN在小数据和大数据环境下都优于Radial Field和GNN。这表明EGNN比GNN更具有数据效率，因为它不需要对数据的旋转和平移进行泛化，同时在大数据环境下集合了GNN的灵活性。

3.2 Graph Autoencoder

自编码器可以在连续的潜在空间中无监督地学习图的表示。本节实验使用EGNN构建一个等变图自编码器并解释图自编码器如何从等变性中受益。
对于一个图$\mathcal{G}=(V,\mathcal{E})$具有节点特征$H\in R^{M\times nf}$和邻接矩阵 A ∈ { 0 , 1 } M × M A\in \{0,1\}^{M\times M} A∈{0,1}M×M，Equivariant Graph Auto-Encoder将$\mathcal{G}$嵌入到潜在空间$z=q(H,A)\in R^{M\times n}$，（其中$M$是节点的数量，$n$是每个节点的embedding_size）使用的数据集不包含节点特征，因此实验只关注邻接矩阵$A$。解码器$g(\cdot )$以嵌入空间$z$作为输入，并输出其重建的邻居矩阵$\hat{A}=g(z)$：
其中 $w$和$b$是唯一的可学习参数，$g_e(\cdot )$ 是应用于每对节点嵌入的解码边函数，它反映了边的概率依赖于节点嵌入之间的相对距离。训练损失为估计边与真实边之间的二元交叉熵：$\mathcal{L}={\sum }_{ij}BCE({\hat{A}}_{ij},A_{ij})$。

3.2.1 The symmetry problem

图神经网络是在图的边和节点上进行卷积，即相同的函数应用于所有边和所有节点。在某些图中可能没有节点的输入特征，因此节点之间的差异仅依赖于它们的边或邻域拓扑。因此，如果两个节点的邻域完全相同，它们的编码嵌入也将相同。Figure 3中提供了一个4节点循环图示例，当在没有节点特征的循环图上运行图神经网络编码器时，每个节点获得完全相同的嵌入，这使得从节点嵌入中重建原始图的边变得不可能。循环图是一个极端的例子，其中所有节点具有完全相同的邻域拓扑，但这些对称性在具有不同边分布的其他图中或即使在包含非唯一节点特征的情况下也可能以不同方式存在。

为了打破图的对称性，Liu等人在图的输入节点特征中引入了从高斯分布中采样的噪声，即$h_i^0\sim N(0,\sigma I)$。这种噪声使得所有节点嵌入具有不同的表示，但这也带来了一个缺点，即网络必须对新引入的噪声分布进行泛化。Equivariant Graph Auto-Encoder保持对采样噪声的平移和旋转等变性，发现这使得泛化变得更加容易。Equivariant Graph Auto-Encoder将这种噪声作为输入坐标$x^0\sim N(0,\sigma I)\in {\mathbb{R}}^{M\times n}$ 输入到EGNN中，输出这些噪声的等变变换$x^L$，这个输出被用作图的嵌入（即$z=x^L$），这是方程9中解码器的输入。

3.2.2 Dataset

1.运行You等人的原始代码生成了社区小型图，这些图包含12到20个节点。2.使用Erdős-Rényi生成模型生成了第二个数据集，采样随机图，初始节点数量为7到16，边的概率为$p_e=0.25$。
我们为两个数据集分别采样了5000个图进行训练，500个用于验证，500个用于测试。每个图被定义为一个邻接矩阵 A ∈ { 0 , 1 } M × M A \in \{0, 1\}^{M \times M} A∈{0,1}M×M。

3.2.3 Implementation details

Equivariant Graph Auto-Encoder由一个EGNN编码器和方程9中的解码器组成。图的边$A_{ij}$被输入为方程3中的边属性$a_{ij}$。为了打破对称性而使用的噪声被输入为第一层的坐标$x^0\sim N(0,\sigma I)\in R^{M\times n}$，并且因为处理的是无特征图，$h^0$被初始化为1。如前所述，编码器输出坐标的等变变换是图嵌入，也是解码器的输入$z=x^L\in R^{M\times n}$。将EGNN与GNN、Noise-GNN、Radial Field进行比较。

3.2.4 Results

在Figure 5的表格中报告了估计边和真实边之间的二元交叉熵损失、%Error定义为错误预测边与潜在边的总数之比以及边分类的F1分数。GNN受到对称性问题的影响，性能最差。当引入噪声（Noise-GNN）时，损失和错误都减少，表明向输入节点添加噪声是有益的。EGNN保持对噪声分布的E(n)等变性并提供了最佳的重建，Erdos&Renyi数据集的错误率为0.11%，接近最优的Community Small数据集为0.06%。

3.3 Molecular data — QM9

QM9数据集是机器学习领域中化学属性预测任务的一个标准数据集。QM9为小分子数据集，这些分子以原子集合的形式表示（每个分子最多包含29个原子），每个原子都有一个相关的3D位置和一个五维的独热编码节点嵌入，这些编码描述了原子类型（H, C, N, O, F）。数据集的标签是每个分子的各种化学属性，这些属性对于原子位置的平移、旋转和反射是不变的。因此，对于E(3)变换不变的模型非常适合这项任务。
训练集包含100K个分子，验证集包含18K个分子，测试集包含13K个分子。每个分子估计了12种化学属性。

3.3.1 Implementation details

EGNN接收每个原子的3D坐标位置作为输入，这些位置作为方程3中的$x_i^0$提供，以及作为输入节点特征的原子属性嵌入$h_i^0$。由于这是一个不变的任务，并且$x^0$位置是静态的，所以不需要运行方程4来更新粒子的位置$x$。EGNN网络由7层组成，每个隐藏层有128个特征，并且使用Swish激活函数作为非线性。一个求和池化操作，前面和后面都有两层MLPs，将EGNN输出的所有节点嵌入$h^L$映射到估计的属性值。EGNN与NMP、Schnet、Cormorant、L1Net、LieConv、DimeNet++、TFN和SE(3)-Tr进行比较。

3.3.2 Results

结果在Table 3中展示。EGNN在这项任务中的表现超过了其他考虑高阶表示的等变网络，而我们只使用了type-0表示（即相对距离）来定义分子的几何结构。