KAN模型

1.简单介绍

今天给大家介绍一篇最近论文《KAN:Kolmogorov-Arnold Networks》，这篇论文对于在人工智能领域深耕的人还是推荐去阅读一下（虽然星主还没读过原文，48页==痛苦）。由于星主还没读过原文，这里只简单介绍一下。

论文地址：https://arxiv.org/pdf/2404.19756

Github：GitHub - KindXiaoming/pykan: Kolmogorov Arnold Networks

文档说明：Welcome to Kolmogorov Arnold Network (KAN) documentation! — Kolmogorov Arnold Network documentation

这篇文章提出了一个叫KAN（Kolmogorov–Arnold Networks）的模型，它对标的是MLPs（多层感知机），这个模型由数学定理Kolmogorov–Arnold启发得出的。该模型最重要的一点就是把激活函数放在了权重上，也就是在权重上应用可学习的激活函数，这些一维激活函数被参数化为样条曲线，从而使得网络能够以一种更灵活、更接近Kolmogorov-Arnold 表示定理的方式来处理和学习输入数据的复杂关系。这里贴一张原论文中MLP和KAN对比的图

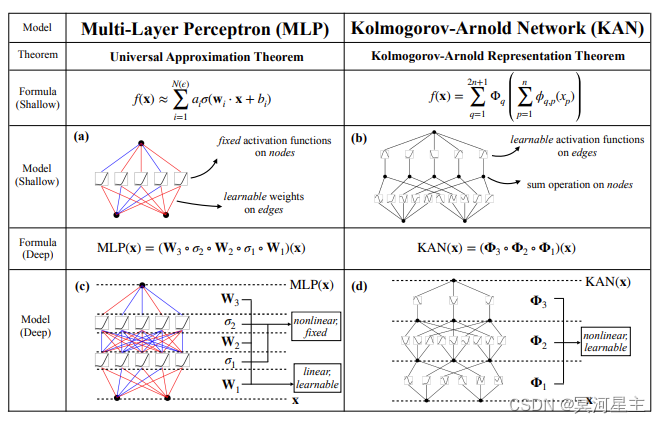
熟悉MLP的人应该清楚，激活函数都是放在了节点上，是不可学习的，星主认为这就是KAN最大的创新点。该模型具有很好的解释性，在某些任务上表现超过了MLP。

2.Kolmogorov-Arnold表示定理

这个定理是由前苏联的两位数学家（Vladimir Arnold 和 Andrey Kolmogorov）提出的，大致说的是：如果是一个多元连续函数，那么可以被写成单变量连续函数和二元加法运算的有限复合。

数学形式如下：

这里的。

简单理解为任何多元连续函数都可以表示为单变量连续函数的两层嵌套叠加（一个单一变量的连续函数和一系列连续的双变量函数的组合），更多的数学原理可以去看维基百科：Kolmogorov–Arnold representation theorem - Wikipedia

3.存在的问题

KAN模型的主要优点就是可解释性好，精度高，但训练速度很慢。在相同参数数量下，KAN的训练速度通常比MLP慢大约10倍。

最后，文中给出了一个训练时选MLP还是KAN的图

好了，其它的内容等星主看完原文后再更新。