机器学习算法之主成分分析法（PCA）

最新推荐文章于 2025-03-05 19:18:27 发布

抱抱宝

最新推荐文章于 2025-03-05 19:18:27 发布

阅读量2.2k

点赞数 29

分类专栏：机器学习文章标签：机器学习算法数学建模 python

本文链接：https://blog.csdn.net/m0_64087341/article/details/143991155

版权

机器学习专栏收录该内容

21 篇文章

订阅专栏

作者名片
🤵‍♂️ 个人主页：@抱抱宝
😄微信公众号：宝宝数模AI（见文末）
✍🏻作者简介：阿里云专家博主 | 持续分享机器学习、数学建模、数据分析、AI人工智能领域相关知识，和大家一起进步！
🐋 如果文章对你有帮助的话，
欢迎👍🏻点赞📂收藏 +关注

文章目录

在机器学习领域，降维是一个非常重要的步骤。它不仅可以减少数据的复杂性，还能在一定程度上去除噪声，提高模型的性能。主成分分析（Principal Component Analysis，简称PCA） 作为一种经典的降维算法，广泛应用于数据预处理、特征提取和可视化等方面。本文将深入介绍PCA的算法原理，并通过案例分析展示其实际应用。

一、算法介绍

主成分分析（PCA）是一种线性降维技术，旨在通过正交变换将高维数据投影到一个低维空间中，同时尽可能保留数据的主要信息。PCA通过找到数据中方差最大的方向（即主成分），将数据沿这些方向进行投影，从而实现降维。

PCA的主要步骤包括：

数据标准化：对原始数据进行均值归一化，使得每个特征的均值为零，方差为一。
计算协方差矩阵：衡量不同特征之间的线性相关性。
求解特征值和特征向量：协方差矩阵的特征值和特征向量决定了主成分的方向和重要性。
选择主成分：根据特征值的大小选择前 $k$ 个主成分。
转换数据：将原始数据投影到选定的主成分上，得到降维后的数据。

二、算法原理

2.1 数据标准化

假设我们有一个包含 $n$ 个样本和 $m$ 个特征的数据集，表示为矩阵 $\in \mathbb{R}^{n \times m}$ 。首先，对每个特征进行标准化处理，使其均值为零，方差为一：

$X_{norm} = \frac{X - \mu}{\sigma}$

其中， $\mu$ 是每个特征的均值， $\sigma$ 是标准差。

2.2 计算协方差矩阵

协方差矩阵 $C$ 用于描述不同特征之间的线性相关性：

$\frac{1}{n-1} X_{norm}^T X_{norm}$

2.3 求解特征值和特征向量

通过对协方差矩阵 $C$ 进行特征值分解，得到特征值 $\lambda_i$ 和对应的特征向量 $v_i$ 。特征值反映了对应特征向量所代表的主成分的重要性。

2.4 选择主成分

选择前 $k$ 个最大的特征值对应的特征向量，构成投影矩阵 $W$ ：

$[v_1, v_2, \dots, v_k]$

2.5 转换数据

将原始数据投影到选定的主成分上，得到降维后的数据 $Y$ ：

$Y = X_{norm} W$

三、案例分析

为了更好地理解PCA的应用，我们将使用Wine（葡萄酒）数据集进行案例分析。Wine数据集包含178个样本，每个样本有13个特征，如酒精含量、苹果酸含量、灰分含量等。由于特征数量较多，我们将通过累计方差贡献度来确定合适的降维维数，并最终进行可视化展示。

3.1 数据准备

首先，导入必要的库，并加载Wine数据集。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler

# 加载Wine数据集
wine = datasets.load_wine()
X = wine.data  # 特征数据
y = wine.target  # 类别标签
feature_names = wine.feature_names
target_names = wine.target_names

3.2 数据标准化

对数据进行标准化处理，使每个特征的均值为零，方差为一。

# 标准化
scaler = StandardScaler()
X_std = scaler.fit_transform(X)

3.3 计算协方差矩阵

计算标准化后的数据的协方差矩阵。

# 计算协方差矩阵
cov_matrix = np.cov(X_std.T)
print("协方差矩阵：\n", cov_matrix)

部分计算结果：

协方差矩阵：
 [[ 1.00564972  0.09493026  0.21273976 -0.31198788  0.27232816  0.29073446
   0.23815287 -0.15681042  0.13747022  0.549451   -0.07215255  0.07275191
   0.64735687]
 [ 0.09493026  1.00564972  0.16497228  0.29013035 -0.05488343 -0.3370606
  -0.41332866  0.29463237 -0.22199334  0.25039204 -0.56446685 -0.37079354
  -0.19309537]
 [ 0.21273976  0.16497228  1.00564972  0.44587209  0.28820583  0.12970824
   0.11572743  0.1872826   0.00970647  0.2603499  -0.07508874  0.00393333
   0.22488969]
 [-0.31198788  0.29013035  0.44587209  1.00564972 -0.0838039  -0.32292752
  -0.353355    0.36396647 -0.19844168  0.01883781 -0.27550299 -0.27833221
  -0.44308618]

3.4 求解特征值和特征向量

对协方差矩阵进行特征值分解，获取特征值和特征向量。

# 特征值分解
eig_vals, eig_vecs = np.linalg.eig(cov_matrix)
print("特征值：\n", eig_vals)
print("特征向量：\n", eig_vecs)

计算结果：

特征值：
 [4.73243698 2.51108093 1.45424187 0.92416587 0.85804868 0.64528221
 0.55414147 0.10396199 0.35046627 0.16972374 0.29051203 0.22706428
 0.25232001]
 部分特征向量：
 [[-0.1443294  -0.48365155  0.20738262 -0.0178563   0.26566365 -0.21353865
  -0.05639636  0.01496997 -0.39613926  0.26628645  0.50861912 -0.22591696
   0.21160473]
 [ 0.24518758 -0.22493093 -0.08901289  0.53689028 -0.03521363 -0.53681385
   0.42052391  0.02596375 -0.06582674 -0.12169604 -0.07528304  0.07648554
  -0.30907994]
 [ 0.00205106 -0.31606881 -0.6262239  -0.21417556  0.14302547 -0.15447466
  -0.14917061 -0.14121803  0.17026002  0.04962237 -0.30769445 -0.49869142
  -0.02712539]
 [ 0.23932041  0.0105905  -0.61208035  0.06085941 -0.06610294  0.10082451
  -0.28696914  0.09168285 -0.42797018  0.05574287  0.20044931  0.47931378
   0.05279942]

3.5 计算累计方差贡献度

为了确定保留多少个主成分，我们需要计算累计方差贡献度，并绘制其随主成分个数变化的曲线。

# 5. 计算累计方差贡献度
explained_variances = eig_vals / np.sum(eig_vals)
cumulative_explained_variances = np.cumsum(explained_variances)

# 绘制累计方差贡献度曲线
plt.figure(figsize=(10, 6))
plt.plot(range(1, len(cumulative_explained_variances)+1), cumulative_explained_variances, marker='o', linestyle='--', color='b')
plt.xlabel('主成分个数')
plt.ylabel('累计方差贡献度')
plt.title('累计方差贡献度随主成分个数的变化')
plt.grid(True)
plt.axhline(y=0.85, color='r', linestyle='-')  # 设定85%的参考线
plt.text(0.5, 0.86, '85% 参考线', color = 'red', fontsize=12)
plt.show()

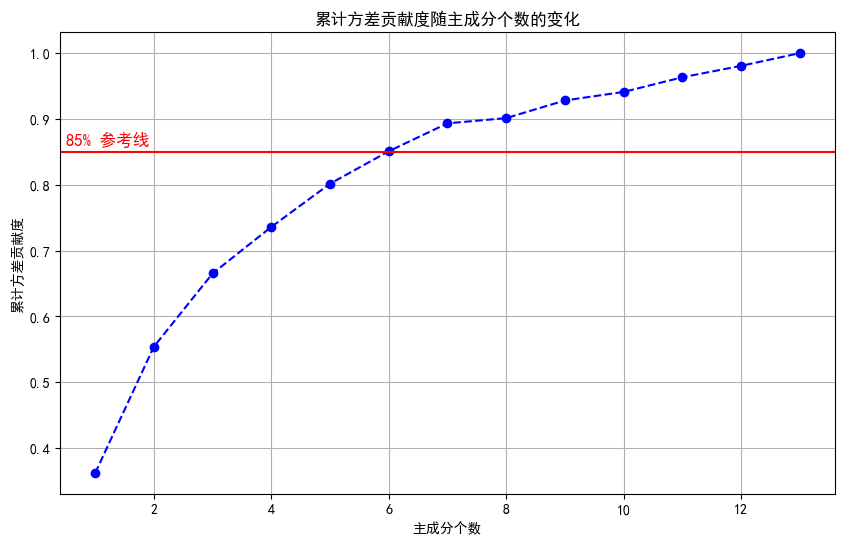
通过观察累计方差贡献度曲线，我们可以选择主成分个数 $k$ ，使得累计方差贡献度达到一个预设的阈值（如85%），从而在尽量保留原始数据信息的前提下，实现有效降维。

3.6 选择主成分

根据累计方差贡献度曲线，我们选择保留前6个主成分，以达到85%的方差解释率。

# 6. 根据累计方差贡献图选择前6个主成分
k = 6
sorted_indices = np.argsort(eig_vals)[::-1]
topk_indices = sorted_indices[:k]
W = eig_vecs[:, topk_indices]
print(f"投影矩阵 W（前{k}个主成分）：\n", W)

计算结果：

投影矩阵 W（前6个主成分）：
 [[-0.1443294  -0.48365155  0.20738262 -0.0178563   0.26566365 -0.21353865]
 [ 0.24518758 -0.22493093 -0.08901289  0.53689028 -0.03521363 -0.53681385]
 [ 0.00205106 -0.31606881 -0.6262239  -0.21417556  0.14302547 -0.15447466]
 [ 0.23932041  0.0105905  -0.61208035  0.06085941 -0.06610294  0.10082451]
 [-0.14199204 -0.299634   -0.13075693 -0.35179658 -0.72704851 -0.03814394]
 [-0.39466085 -0.06503951 -0.14617896  0.19806835  0.14931841  0.0841223 ]
 [-0.4229343   0.00335981 -0.1506819   0.15229479  0.10902584  0.01892002]
 [ 0.2985331  -0.02877949 -0.17036816 -0.20330102  0.50070298  0.25859401]
 [-0.31342949 -0.03930172 -0.14945431  0.39905653 -0.13685982  0.53379539]
 [ 0.0886167  -0.52999567  0.13730621  0.06592568  0.07643678  0.41864414]
 [-0.29671456  0.27923515 -0.08522192 -0.42777141  0.17361452 -0.10598274]
 [-0.37616741  0.16449619 -0.16600459  0.18412074  0.10116099 -0.26585107]
 [-0.28675223 -0.36490283  0.12674592 -0.23207086  0.1578688  -0.11972557]]

3.7 转换数据

将原始数据投影到选定的主成分上，得到降维后的数据。

# 7. 转换数据
Y = X_std.dot(W)
print("降维后的数据（前6个样本）：\n", Y[:6])

计算结果:

降维后的数据（前6个样本）：
 [[-3.31675081 -1.44346263  0.16573904 -0.21563119 -0.69304284 -0.22388013]
 [-2.20946492  0.33339289  2.02645737 -0.29135832  0.25765463 -0.92712024]
 [-2.51674015 -1.0311513  -0.98281867  0.72490231  0.25103312  0.54927605]
 [-3.75706561 -2.75637191  0.17619184  0.56798331  0.31184159  0.114431  ]
 [-1.00890849 -0.86983082 -2.02668822 -0.40976579 -0.2984575  -0.4065196 ]
 [-3.05025392 -2.12240111  0.62939583 -0.51563749  0.63201873  0.12343056]]

3.8 可视化

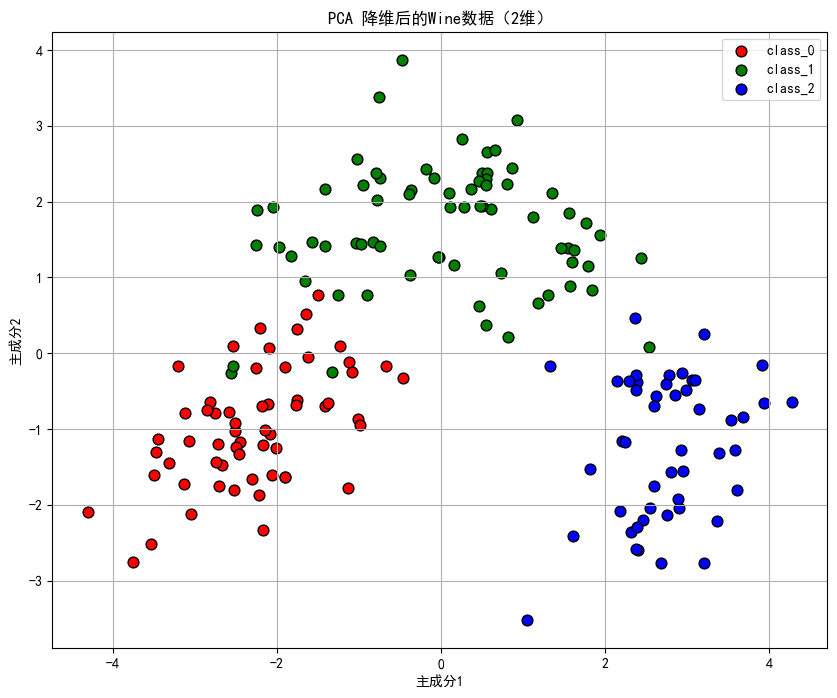
由于选择了6个主成分，为了便于可视化，我们可以进一步将数据降维到2维，或者使用前两个主成分进行二维可视化。

# 8. 可视化（选择前2个主成分）
W_2d = eig_vecs[:, sorted_indices[:2]]
Y_2d = X_std.dot(W_2d)

plt.figure(figsize=(10, 8))
for target, color, label in zip([0,1,2], ['r', 'g', 'b'], target_names):
    plt.scatter(Y_2d[y == target, 0], Y_2d[y == target, 1], 
                c=color, label=label, edgecolor='k', s=60)
plt.xlabel('主成分1')
plt.ylabel('主成分2')
plt.title('PCA 降维后的Wine数据（2维）')
plt.legend()
plt.grid(True)
plt.show()

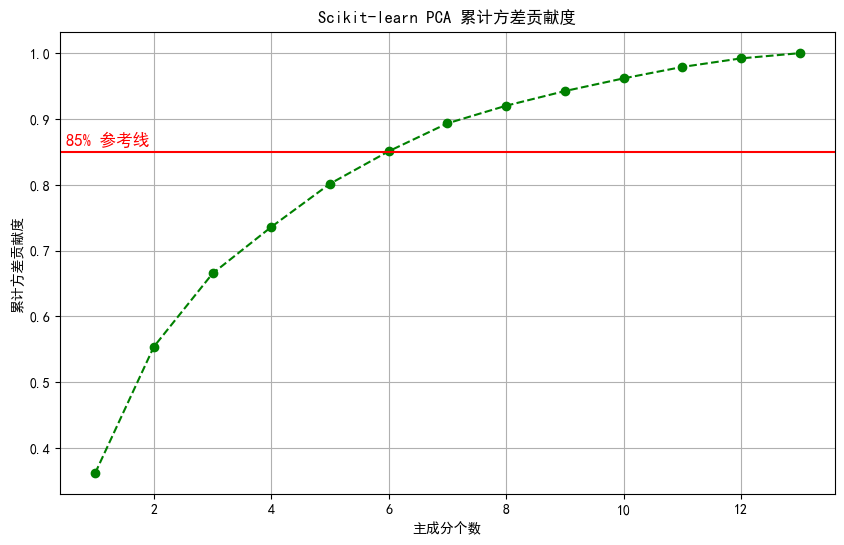
3.9 使用Scikit-learn实现PCA

为了验证手动计算的结果，我们还可以使用scikit-learn库中的PCA模块进行降维，并绘制累计方差贡献度曲线。

# 9. 使用Scikit-learn的PCA
pca = PCA(n_components=13)  # 保留所有主成分以计算累计方差
pca.fit(X_std)
cumulative_explained_variances_sklearn = np.cumsum(pca.explained_variance_ratio_)

# 绘制累计方差贡献度曲线
plt.figure(figsize=(10, 6))
plt.plot(range(1, len(cumulative_explained_variances_sklearn)+1), cumulative_explained_variances_sklearn, marker='o', linestyle='--', color='g')
plt.xlabel('主成分个数')
plt.ylabel('累计方差贡献度')
plt.title('Scikit-learn PCA 累计方差贡献度')
plt.grid(True)
plt.axhline(y=0.85, color='r', linestyle='-')  # 设定85%的参考线
plt.text(0.5, 0.86, '85% 参考线', color = 'red', fontsize=12)
plt.show()

# 选择前6个主成分
pca = PCA(n_components=6)
Y_sklearn = pca.fit_transform(X_std)
print("scikit-learn降维后的数据（前6个主成分，前6个样本）：\n", Y_sklearn[:5])

# 使用前两个主成分进行可视化
pca_2d = PCA(n_components=2)
Y_sklearn_2d = pca_2d.fit_transform(X_std)

# 可视化
plt.figure(figsize=(10, 8))
for target, color, label in zip([0,1,2], ['r', 'g', 'b'], target_names):
    plt.scatter(Y_sklearn_2d[y == target, 0], Y_sklearn_2d[y == target, 1], 
                c=color, label=label, edgecolor='k', s=60)
plt.xlabel('主成分1')
plt.ylabel('主成分2')
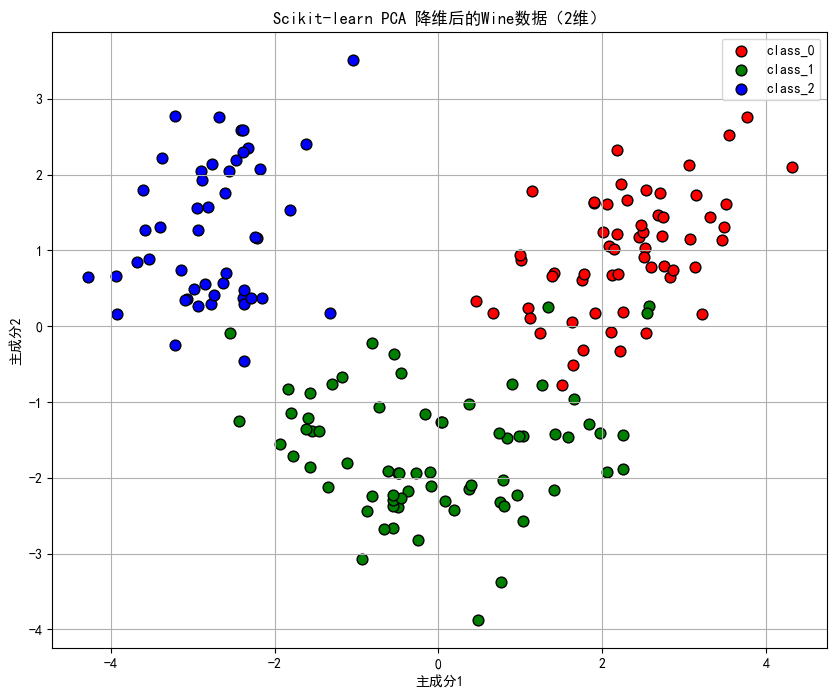
plt.title('Scikit-learn PCA 降维后的Wine数据（2维）')
plt.legend()
plt.grid(True)
plt.show()

scikit-learn降维后的数据（前6个主成分，前6个样本）：
 [[ 3.31675081  1.44346263 -0.16573904 -0.21563119  0.69304284  0.22388013]
 [ 2.20946492 -0.33339289 -2.02645737 -0.29135832 -0.25765463  0.92712024]
 [ 2.51674015  1.0311513   0.98281867  0.72490231 -0.25103312 -0.54927605]
 [ 3.75706561  2.75637191 -0.17619184  0.56798331 -0.31184159 -0.114431  ]
 [ 1.00890849  0.86983082  2.02668822 -0.40976579  0.2984575   0.4065196 ]]