概率论-条件数学期望（复习笔记自用）

条件分布

实际上，求条件期望就是在新的概率空间上进行计算,即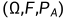，因此也继承了期望的所有性质

• 如果，则E(X)=Eg(Y)

• 使用全概率公式，可以容易得到证明

• 理解，找到共性

• 正态分布的优良性质：正态分布的条件分布仍为正态分布

条件密度

• 公式的证明充分体现出微分法的优势

• 理解：对于固定的y,条件密度是x的函数且和f(x,y)只相差常数因子（充分理解这句话！！）

条件数学期望

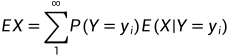
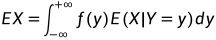
• m(y)=E(X|Y=y)是已知Y=y时X的数学期望，m(Y)是已知Y时X的条件数学期望

• 计算方法：要求条件数学期望E(X|Y),只需要先计算E(X|Y=y),然后将计算结果中的y替换成Y即可。其中最重要的公式重期望公式也就不难以理解EX=E(E(X|Y))

极值的分布

（186）非常清晰，此处略

关于次序统计量的初步研究，主要运用微分法