——————————————————————————————————————————————————————————
条件期望公式:
E
(
X
∣
Y
=
y
)
=
∑
x
x
p
(
X
=
x
∣
Y
=
y
)
\begin{align}E\left ( X|Y=y \right ) &= \color{blue} \sum_{x}^{} xp\left ( X=x|Y=y \right ) \\ \end{align}
E(X∣Y=y)=x∑xp(X=x∣Y=y)
p
(
X
=
x
∣
Y
=
y
)
p\left ( X=x|Y=y \right )
p(X=x∣Y=y)是二维随机变量联合分布的条件概率
全期望公式:
E
(
X
)
=
E
(
E
(
X
∣
Y
)
)
=
∑
y
E
(
X
∣
Y
=
y
)
p
(
Y
=
y
)
\begin{align} E\left ( X \right ) &= E\left ( E\left ( X|Y \right ) \right ) \\ &={\color{blue} \sum_{y}^{} E\left ( X|Y=y \right ) p\left ( Y=y \right ) } \end{align}
E(X)=E(E(X∣Y))=y∑E(X∣Y=y)p(Y=y)
E
(
X
∣
Y
=
y
)
E\left ( X|Y=y \right )
E(X∣Y=y)是条件期望
全期望公式与全概率公式相似,通过将引入随机变量Y的样本空间划分成不同的子空间,然后计算每个子空间Yi对应的X的条件数学期望,X的总期望就是X的条件期望的加权平均。
——————————————————————————————————————————————————————————
条件期望和全期望图解:
原图链接:如何更好的理解双期望(全期望)定理
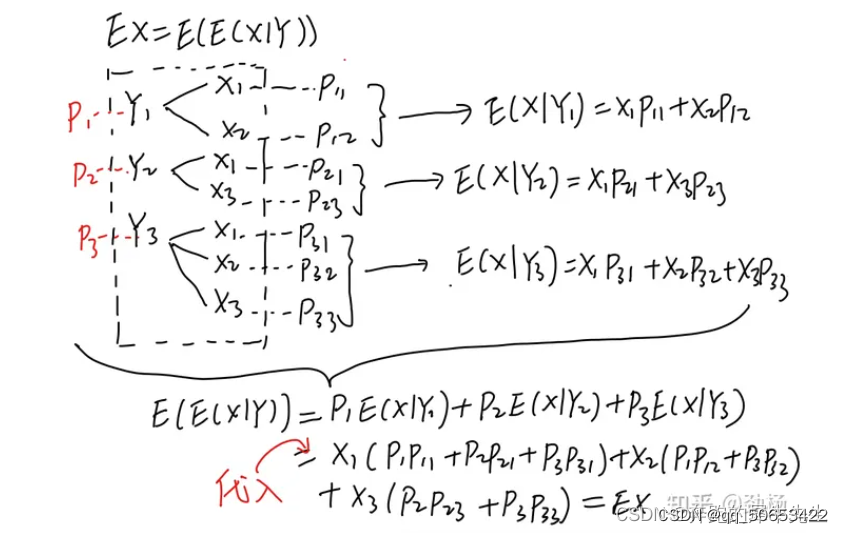
注意这里的
p
i
j
p_{ij}
pij是条件概率,代入的那个步骤是全概率公式
——————————————————————————————————————————————————————————
条件期望和全期望举例:
原文链接:通俗理解条件概率、条件期望、条件方差
一个年级有两个班,分别是A班和B班,A班有3人,三人的分数分别为
x
11
x_{11}
x11、
x
12
x_{12}
x12、
x
13
x_{13}
x13,B班有4人,四人的分数分别为
x
21
x_{21}
x21、
x
22
x_{22}
x22、
x
23
x_{23}
x23、
x
24
x_{24}
x24。那么:
期望:
①A班的班级平均分为
x
‾
A
=
x
11
+
x
12
+
x
13
3
{\overline{x} _{{\tiny A}}} =\frac{x_{11} +x_{12}+ x_{13} }{3}
xA=3x11+x12+x13 ,这是A班的条件期望 E(分数,班级=A班)。
②B班的班级平均分为 x ‾ B = x 21 + x 22 + x 23 + x 24 4 {\overline{x}_{{\tiny B} }} =\frac{x_{21} +x_{22}+ x_{23}+ x_{24}}{4} xB=4x21+x22+x23+x24,这是B班的条件期望 E(分数,班级=B班)。
③年级总的平均分为
x
‾
=
x
11
+
x
12
+
x
13
+
x
21
+
x
22
+
x
23
+
x
24
7
=
x
11
+
x
12
+
x
13
3
×
3
7
+
x
21
+
x
22
+
x
23
+
x
24
4
×
4
7
\begin{align}{\overline{x}} & = \frac{x_{11} +x_{12}+ x_{13}+x_{21} +x_{22}+ x_{23}+ x_{24}}{7} \\&=\frac{x_{11} +x_{12}+ x_{13}}{3}\times \frac{3}{7} +\frac{x_{21} +x_{22}+ x_{23}+ x_{24}}{4} \times \frac{4}{7}\end{align}
x=7x11+x12+x13+x21+x22+x23+x24=3x11+x12+x13×73+4x21+x22+x23+x24×74,这是总体的期望,此处体现了加权平均的思想。也对应一句话——总体的期望是部分条件期望的期望。
——————————————————————————————————————————————————————————
题目:连续地做每次成功的概率为p的独立试验,直至有k次连续成功.求所需试验次数的期望
这个题目据说有多种解法(但是我菜菜解法一还是看了zh才会的T_T)
解法一(全期望公式):
其实我不太懂为什么认为这是全期望解法,因为我印象中的全期望里的关联变量Y,是有限可数个值,这里的关联变量Y是
N
k
−
1
N_{k-1}
Nk−1我实在是想象不出来怎么解释。
感觉更像是期望pd (那种蜗牛爬树),
,
p
+
(
1
−
p
)
(
1
+
E
(
N
k
)
)
,p+\left ( 1-p \right ) \left ( 1+E(N_{k} ) \right )
,p+(1−p)(1+E(Nk))就是dp[k-1],但是蜗牛爬树这种递推式期望的数学原理我又搞不太清楚,怎么没有什么递推期望公式
设随机变量
N
k
N_{k}
Nk:事件连续k次成功所需试验的次数
N
k
−
1
N_{k-1}
Nk−1:事件连续k-1次成功所需试验的次数
(
N
k
N_{k}
Nk这个整体是随机变量(即常提的X),k就只是一个用来泛化的参数;
N
k
−
1
N_{k-1}
Nk−1同理)
随机变量拆解:
N
k
=
E
(
N
k
∣
N
k
−
1
)
=
N
k
−
1
+
p
+
(
1
−
p
)
(
1
+
E
(
N
k
)
)
\begin{align} N_{k} &=E\left ( N_{k}|N_{k-1} \right ) \\ &=\color{blue} N_{k-1} +p+\left ( 1-p \right )\left ( 1+E\left ( N_{k} \right ) \right ) \end{align}
Nk=E(Nk∣Nk−1)=Nk−1+p+(1−p)(1+E(Nk))
根据全期望公式有:
E
(
N
k
)
=
E
(
E
(
N
k
∣
N
k
−
1
)
)
=
E
(
N
k
−
1
+
p
+
(
1
−
p
)
(
1
+
E
(
N
k
)
)
)
=
E
(
N
k
−
1
)
+
p
+
(
1
−
p
)
(
1
+
E
(
N
k
)
)
\begin{align} E\left ( N_{k} \right ) &= E\left ( E\left ( N_{k}|N_{k-1} \right ) \right ) \\ &=E\left ( N_{k-1} +p+\left ( 1-p \right )\left ( 1+E\left ( N_{k} \right ) \right ) \right ) \\ &=\color{blue} E\left ( N_{k-1} \right )+p+\left ( 1-p \right ) \left ( 1+E(N_{k} ) \right ) \end{align}
E(Nk)=E(E(Nk∣Nk−1))=E(Nk−1+p+(1−p)(1+E(Nk)))=E(Nk−1)+p+(1−p)(1+E(Nk))
整理解得:
E
(
N
k
)
=
1
p
E
(
N
k
−
1
)
+
1
p
\begin{align} \color{blue} E\left ( N_{k} \right ) &=\color{blue} \color{blue} \color{blue} \frac{1}{p} E(N_{k-1} ) +\frac{1}{p} \end{align}
E(Nk)=p1E(Nk−1)+p1
(11)式是数列的递推式(自变量是k)
(如果数列的第n项an+1与它前一项an或几项的关系可以用一个式子来表示,那么这个公式叫做这个数列的递推公式。)
根据上式,递推有:
E
(
N
1
)
=
1
p
E
(
N
2
)
=
1
p
(
1
p
)
+
1
p
=
1
p
2
+
1
p
E
(
N
3
)
=
1
p
(
1
p
2
+
1
p
)
+
1
p
=
1
p
3
+
1
p
2
+
1
p
\begin{align} E\left ( N_{1} \right ) &=\frac{1}{p}\\E\left ( N_{2} \right ) &=\frac{1}{p} (\frac{1}{p})+\frac{1}{p}\\ &=\frac{1}{p^{2} }+\frac{1}{p}\\E\left ( N_{3} \right ) &=\frac{1}{p} (\frac{1}{{p^{2} } } +\frac{1}{p})+\frac{1}{p}\\ &=\frac{1}{p^{3} }+\frac{1}{p^{2} }+\frac{1}{p} \end{align}
E(N1)E(N2)E(N3)=p1=p1(p1)+p1=p21+p1=p1(p21+p1)+p1=p31+p21+p1
一般地,数列
E
(
N
k
)
E\left ( N_{k} \right )
E(Nk)的通项公式为:
E
(
N
k
)
=
1
p
+
1
p
2
+
⋅
⋅
⋅
+
1
p
k
\begin{align} \color{blue} E\left ( N_{k} \right ) &=\color{blue} \frac{1}{p}+\frac{1}{p^{2} }+\cdot \cdot \cdot +\frac{1}{p^{k} } \end{align}
E(Nk)=p1+p21+⋅⋅⋅+pk1
(17)式泛用于:重复独立试验(不单单是伯努利试验,即试验结果>=2,公式结果和程序模拟结果差不多),某事件连续k次发生。因为某事件的发生与不发生实际上就是一个事件的示性函数
书本上的:试验结果只有两种–伯努利试验–伯努利分布
我想的:试验结果大于两种–不是伯努利试验–但是研究的事件是示性(感觉我就是钻牛角尖了,不想了,好像试验的样本空间是可以根据研究目的调整的,发生与不发生就是两种试验结果了,伯努利分布就有了。不管色子可以掷6还是n面,但对于试验目的,只有我要得到的一面,和其他面两种结果。。。。)
——————————————————————————————————————————————————————————
其实一开始我在第一步就想不出来了为什么
N
k
N_{k}
Nk一个随机变量有可列个值就等于一个期望
(没想到期望也可以是随机变量,就像样本均值也是一个随机变量,那全期望实际上也可以看成是一个普通期望公式)
我一开始想的条件期望是:
随机变量Y:第一次试验的结果(Y=0事件不发生,1事件发生)
E
(
N
k
)
=
∑
y
E
(
N
k
∣
Y
=
y
)
p
(
y
)
=
E
(
N
k
∣
Y
=
0
)
p
(
Y
=
0
)
+
E
(
N
k
∣
Y
=
1
)
p
(
Y
=
1
)
=
(
1
+
E
(
N
k
)
)
(
1
−
p
)
+
(
1
+
p
k
−
1
(
k
−
1
)
+
∑
i
=
1
k
−
1
p
i
(
i
+
E
(
N
k
)
)
)
p
\begin{align} E\left ( N_{k} \right ) &=\sum_{y}^{} E\left ( N_{k} |Y=y \right ) p\left ( y \right ) \\ &=E\left ( N_{k} |Y=0 \right )p\left ( Y=0 \right ) +E\left ( N_{k} |Y=1 \right )p\left ( Y=1 \right )\\ &=(1+E\left ( N_{k} \right ) )\left ( 1-p \right ) +(1+p^{k-1}(k-1)+ \sum_{i=1}^{k-1}p^{i}\left ( i+ E\left ( N_{k} \right )\right ) )p \end{align}
E(Nk)=y∑E(Nk∣Y=y)p(y)=E(Nk∣Y=0)p(Y=0)+E(Nk∣Y=1)p(Y=1)=(1+E(Nk))(1−p)+(1+pk−1(k−1)+i=1∑k−1pi(i+E(Nk)))p
记得当时是从k=1一直推到k=4,结果越来越长,没有模拟验证过,不知道对不对
这种解法,当k比较小的时候还好,k比较大的时候计算量多
这可能就是我概率论的上限了,so sad
相关链接转载:
抛一枚硬币直到出现连续 n 次正面向上
抛硬币第⼀次出现连续两个正⾯的期望次数
——————————————————————————————————————————————————————————
重复试验,求停止试验时试验的期望次数





















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








