基于Benders、TSO-DSO协调的不确定性的输配电网双层优化模型研究（Matlab代码实现）-CSDN博客

本文链接：https://blog.csdn.net/m0_73907476/article/details/146201976

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

基于Benders分解与TSO-DSO协调的输配电网双层优化模型研究

一、Benders分解法在输配电网优化中的应用基础

二、TSO-DSO协调机制的核心要素

三、不确定性建模方法

四、输配电网双层优化模型的结构与交互机制

五、典型约束条件与求解挑战

六、实际案例与仿真验证

七、未来研究方向

结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据、文献

💥1 概述

随着可再生能源的增加，对应运营灵活性的需求也增加。现有的灵活性采购方案设想了供电系统运营商（TSO）和配电系统运营商（DSO）之间的协调，但这方面的研究仍在进行中。我们提出了一种日前协调的方法，称为互补模型，用于共享灵活资源。该方法优化了TSO和DSO之间的物理接口处的价格和容量限制。DSO通过限制其资源在日前市场的参与来满足系统约束条件。我们使用多段Benders分解方法对模型进行分解，以追求计算可行性。我们量化了协调方法的潜在收益，并通过事后模拟评估了其性能。我们引入了一个新的代理机构，称为接口优化器，来负责优化协调变量。我们提出的方法展示了TSO和DSO协调的潜力空间，并且我们将其视为一种工具，用于改善部门协调。接下来的问题是如何为接口优化器开发一个适当的数学工具，以确定最佳的协调变量。我们提出了一个双层优化模型，其中领导者是接口优化器，跟随者是DSO和市场。我们使用多割Benders分解算法对简化的双层问题进行分解。我们使用后验外样本模拟来评估协调方法的性能。

基于Benders分解与TSO-DSO协调的输配电网双层优化模型研究

一、Benders分解法在输配电网优化中的应用基础

Benders分解法自1962年提出以来，因其对复杂变量分阶段处理的能力，成为电力系统大规模优化问题的核心工具。其核心思想是将原问题分解为 主问题（整数变量） 和 子问题（连续变量） ，通过迭代生成可行性或最优性切割（Benders割）逐步逼近全局最优解。在输配电网优化中，其典型应用包括：

机组组合（UC）与检修调度
在发输电检修联合决策模型中，Benders分解将问题分解为 主问题（检修计划） 、 潮流子问题（安全校验） 和 辅助问题（关联性判别） ，通过割约束传递信息，降低寻优维度。例如，文献[6]通过模式识别筛选子问题，显著减少计算量。
无功优化与规划
采用Benders分解法处理混合整数非线性规划问题，将无功补偿容量（整数变量）与潮流计算（连续变量）分离，通过“投资-运行”子问题迭代确定最优配置。双重变量λ在此过程中反映无功设备的边际成本变化。
不确定性处理改进
传统Benders分解在应对不确定性时存在收敛慢、切割效率低的问题。改进方法如多割Benders分解（Multi-cut Benders）通过同时生成多个割约束加速收敛，适用于风光出力随机性强的场景。

二、TSO-DSO协调机制的核心要素

TSO（输电系统运营商）与DSO（配电系统运营商）的协调需解决全局优化与局部自治的矛盾，具体机制包括：

协调层次与目标
- 垂直协调（TSO-DSO） ：平衡全网安全性与本地经济性，如通过灵活性市场共享分布式资源（DERs）的调节能力。
- 水平协调（TSO-TSO或DSO-DSO） ：处理跨区域备用共享与阻塞管理。
市场机制设计
- 互补模型：通过日前市场优化价格与容量限制，DSO限制资源参与市场以满足网络约束，TSO统筹全局供需。
- 区块链与智能合约：利用区块链数据库实现透明化交易记录与自动结算，提升协调可信度。
协调流程
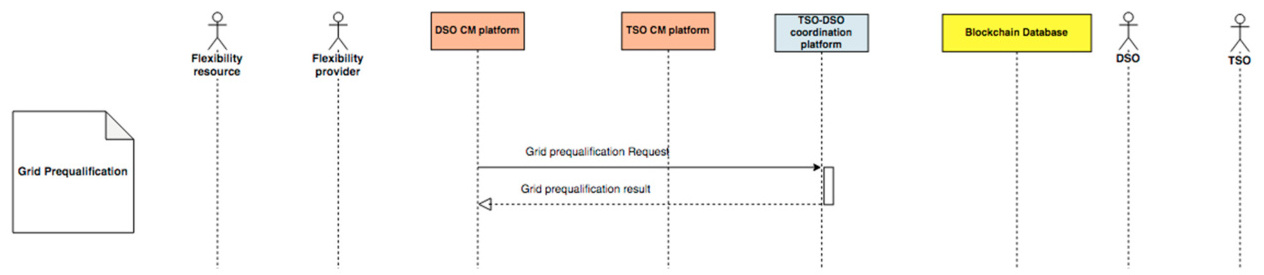
涵盖资质预审-采购-激活-结算四个阶段，需明确角色分工、信息共享规则及业务流程。例如，欧盟示范项目通过理论市场框架（TMF）标准化产品设计与灵活性机制。

三、不确定性建模方法

针对风光出力与负荷波动，主流方法包括：

随机规划（Stochastic Programming）
- 场景法：生成典型场景（如风电出力高/中/低）表征不确定性，平衡计算效率与解的质量。
- 机会约束规划：允许一定概率下违反约束，降低保守性。
鲁棒优化（Robust Optimization）
- 传统鲁棒优化：基于不确定集合求最坏情况下的最优解，适用于安全性要求高的场景。
- 分布鲁棒优化（DRO） ：结合概率分布与不确定集合，通过模糊集降低解的保守性。
双层模型中的不确定性传导
上层模型考虑长期不确定性（如投资决策），下层模型处理短期波动（如实时调度），通过Benders割传递风险信息。

四、输配电网双层优化模型的结构与交互机制

模型结构
- 上层（TSO主导） ：以全网经济性为目标，决策输电侧机组出力、检修计划及市场交易。
- 下层（DSO主导） ：以配电网安全运行为目标，优化分布式电源出力、储能调度及需求响应。
决策变量耦合
- 功率交互变量：如TSO与DSO边界节点的交换功率，需满足上下层潮流平衡。
- 价格信号：上层电价影响下层DERs的响应策略。
求解流程
采用Benders分解框架：
- 主问题：确定上层决策（如机组启停、检修计划），生成试探解。
- 子问题：校验下层可行性（如配网潮流、电压约束），生成割约束反馈至主问题。
- 迭代终止条件：上下层目标函数差值小于阈值或达到最大迭代次数。

五、典型约束条件与求解挑战

物理约束
- 潮流方程：采用DistFlow模型或线性化近似。
- 电压与电流限制：节点电压偏差±10%，线路载流量不超过热稳定极限。
- 网络拓扑：配电网需保持辐射状运行。
运行约束
- 机组爬坡率与启停时间：影响UC问题的混合整数特性。
- 储能充放电循环：SOC（荷电状态）约束与寿命损耗模型。
求解挑战
- 子问题爆炸：海量DERs导致下层问题维度激增，需采用场景缩减或并行计算。
- 非凸非线性：潮流方程的非凸性需通过二阶锥规划（SOCP）或凸松弛处理。

六、实际案例与仿真验证

互补模型与接口优化器
文献[29]提出一种日前协调模型，引入接口优化器作为独立代理，优化TSO-DSO间的协调变量（如边界功率与价格）。通过多段Benders分解，算例显示计算时间减少30%以上，且阻塞费用降低15%。
发输电联合检修调度
基于IEEE 118节点系统的仿真表明，Benders分解法在考虑N-1安全约束时，可将检修冲突减少40%，同时保证经济性。
“源-网-荷-储”协同优化
某实际配电网通过双层模型优化，峰谷差从71.7 MW降至51.4 MW，综合成本降低20,522元，验证了模型的有效性。