用数据选择器实现组合逻辑函数
基本原理
数据选择器输出信号逻辑表达式的一般形式
4 选 1 数据选择器输出信号的逻辑表达式
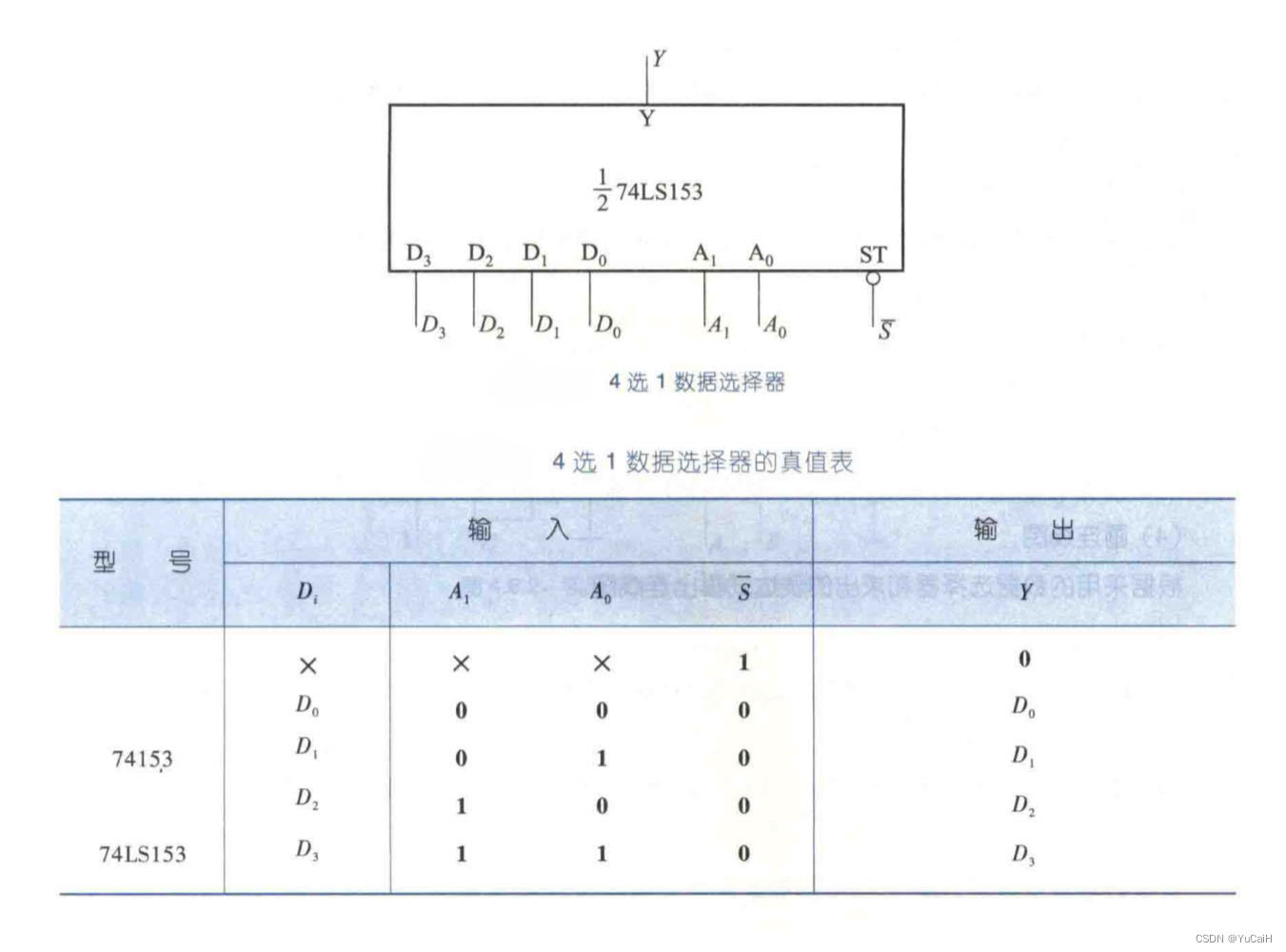
令 S = 1 S=1 S=1 即 S ‾ = 0 \overline{S}=0 S=0 ,选择器使能,则可得 4 选 1 数据选择器输出信号的逻辑表达式为:
Y Y Y = A 1 ‾ \overline{A_1} A1 A 0 ‾ \overline{A_0} A0 D 0 D_0 D0 + A 1 ‾ \overline{A_1} A1 A 0 A_0 A0 D 1 D_1 D1 + A 1 A_1 A1 A 0 ‾ \overline{A_0} A0 D 2 D_2 D2 + A 1 A_1 A1 A 0 A_0 A0 D 3 D_3 D3
= m 0 D 0 + m 1 D 1 + m 2 D 2 + m 3 D 3 m_0D_0 + m_1D_1+ m_2D_2+ m_3D_3 m0D0+m1D1+m2D2+m3D3
= ∑ 0 3 m i D i \sum_0^3m_iD_i ∑03miDi
➡️ m 选 1 数据选择器输出信号的逻辑表达式中
m
=
2
n
m=2^n
m=2n , n 是选择器地址码的位数,也就是地址变量的个数,其输出信号逻辑表达式的一般表达形式为:
Y
=
∑
0
m
−
1
m
i
D
i
=
∑
0
2
n
−
1
m
i
D
i
Y=\sum_0^{m-1}m_iD_i = \sum_0^{2^n-1}m_iD_i
Y=0∑m−1miDi=0∑2n−1miDi
数据选择器输出信号逻辑表达式的主要特点
- 具有标准与或表达式的形式
- 提供了地址变量(选择控制信号)的全部最小项
- 一般情况下, D i D_i Di 可以当成一个变量处理
- 受选通(使能)信号 S ‾ \overline{S} S 的控制,当 S ‾ = 0 \overline{S}=0 S=0 时有效, S ‾ = 1 \overline{S}=1 S=1 时 Y = 0 Y=0 Y=0
组合逻辑函数的标准表达形式
任何组合逻辑函数都是由它的最小项构成的,都可以表示成为最小项的之和的标准形式
用数据选择器实现组合逻辑函数的基本步骤
-
确定数据选择器的型号
根据 $n=k-$1或 n = k n=k n=k 确定数据选择器的型号(n:选择器地址码,k:函数的变量个数)
-
写出逻辑函数的标准与或式和输出信号表达式
-
确定选择器各个输入变量的表达式
-
根据采用的数据选择器和求出的表达式画出连线图
应用举例
【例1】
用数据选择器实现函数 F = A B + B C + A C F=AB + BC + AC F=AB+BC+AC
代数法求解
-
Step1:根据 n = k − 1 n=k-1 n=k−1 或 n = k n=k n=k 确定数据选择器的型号
有 A 、 B 、 C A、B、C A、B、C 三个变量,故 k = 3 k=3 k=3 ,可以选用 8 选 1 数据选择器(74LS151)
-
Step2:写出逻辑函数的最小项表达式(标准与或式)
Y = A B + B C + A C Y=AB+BC+AC Y=AB+BC+AC
= A ‾ B C + A B ‾ C + A B C ‾ + A B C = \overline{A}BC + A\overline{B}C + AB\overline{C} + ABC =ABC+ABC+ABC+ABC
= ∑ m ( 3 , 5 , 6 , 7 ) =\sum m(3,5,6,7) =∑m(3,5,6,7)
-
Step3:写出数据选择器(8选1)的输出信号表达式
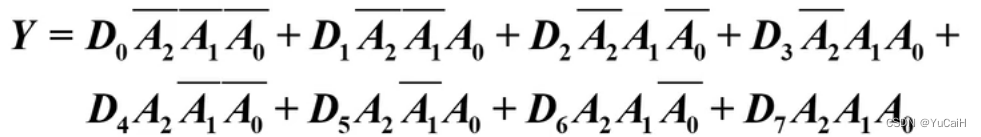
-
Step4:令 A 2 = A A_2 = A A2=A , A 1 = B A_1 = B A1=B, A 0 = C A_0 = C A0=C

与逻辑函数的最小项表达式对比得:

-
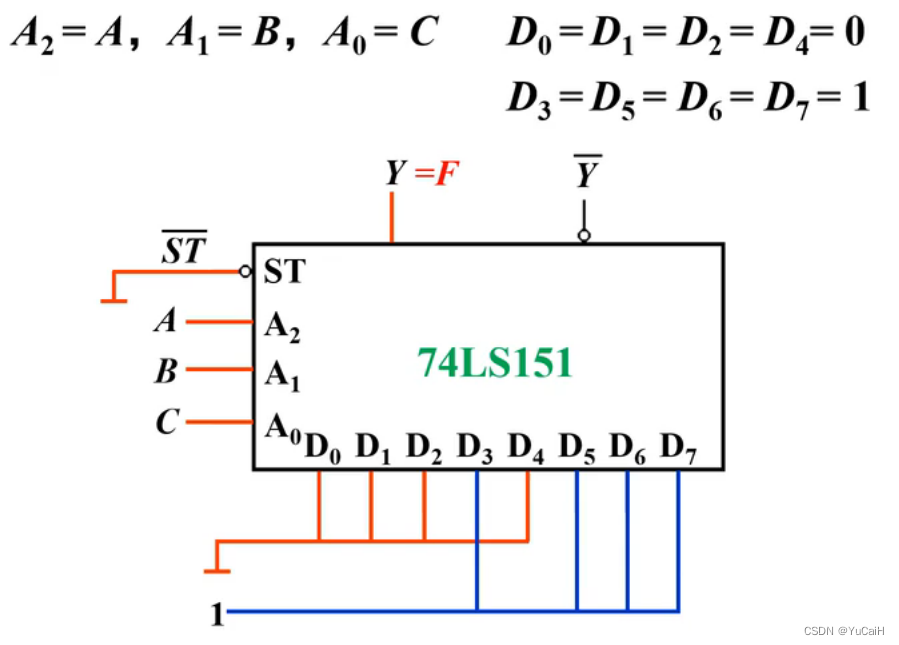
Step5:画连线图
卡诺图发求解
-
Step1:选择数据选择器
选用 74LS151
-
Step2:画出 F 和数据选择器输出 Y 的卡诺图

-
Step3:比较逻辑函数 F 和 Y 的卡诺图
要使 Y = F Y=F Y=F ,则令 A 2 = A A_2 = A A2=A , A 1 = B A_1 = B A1=B, A 0 = C A_0 = C A0=C
则 D 0 = D 1 = D 2 = D 4 = 0 D_0=D_1=D_2=D_4=0 D0=D1=D2=D4=0 、 D 3 = D 5 = D 6 = D 7 = 1 D_3=D_5=D_6=D_7=1 D3=D5=D6=D7=1
-
Step4:画连线图
【例2】
用数据选择器 74LS153 实现函数 F = A B + A C + B C F=AB+AC+BC F=AB+AC+BC
公式法(拼凑法)
-
Step1:根据 n = k − 1 n=k-1 n=k−1 或 n = k n=k n=k 确定数据选择器的型号
因为 n = k − 1 n=k-1 n=k−1 = 3 -1 = 2,可用数据选择器 74LS153
-
Step2:标准与或式 & 数据选择器输出表达式
F = A ‾ B C + A B ‾ C + A B C ‾ + A B C F= \overline{A}BC + A\overline{B}C + AB\overline{C} + ABC F=ABC+ABC+ABC+ABC
Y Y Y = A 1 ‾ \overline{A_1} A1 A 0 ‾ \overline{A_0} A0 D 0 D_0 D0 + A 1 ‾ \overline{A_1} A1 A 0 A_0 A0 D 1 D_1 D1 + A 1 A_1 A1 A 0 ‾ \overline{A_0} A0 D 2 D_2 D2 + A 1 A_1 A1 A 0 A_0 A0 D 3 D_3 D3
-
Step3:确定输入变量和地址码的对应关系
令 A 1 = A A_1 = A A1=A、 A 0 = B A_0=B A0=B
Y Y Y = A ‾ \overline{A} A B ‾ \overline{B} B D 0 D_0 D0 + A ‾ \overline{A} A B B B D 1 D_1 D1 + A A A B ‾ \overline{B} B D 2 D_2 D2 + A A A B B B D 3 D_3 D3
要令 Y = F Y=F Y=F ,则 D 0 = 0 D_0=0 D0=0 , D 1 = C D_1=C D1=C, D 2 = C D_2=C D2=C, D 3 = C ‾ + C = 1 D_3=\overline{C} + C=1 D3=C+C=1
-
Step4:画连线图
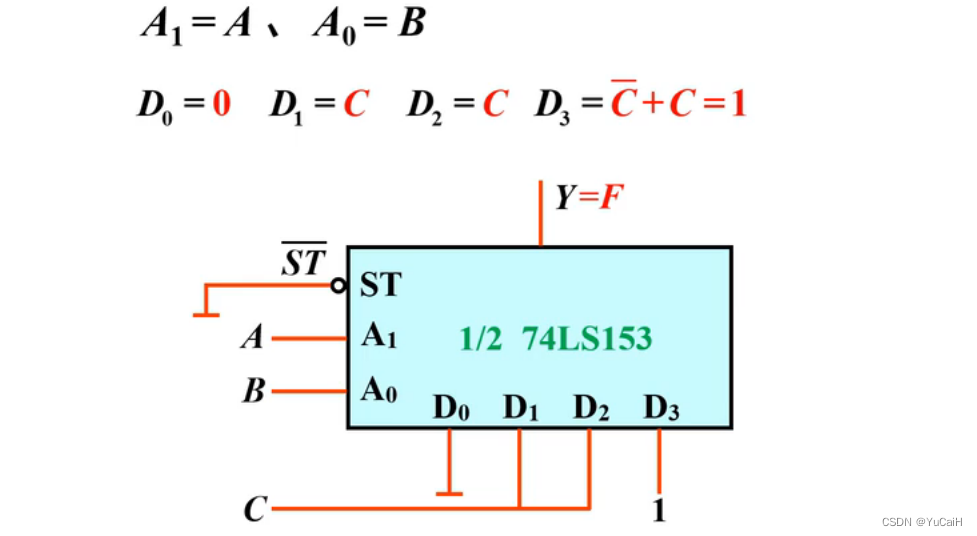
图形法(降维法)
-
Step1:确定数据选择器的型号
使用数据选择器 74LS153
-
Step2:通过降维真值表画出 F 的降维卡诺图&数据选择器输出 Y 的卡诺图


-
Step3:比较逻辑函数 F 和 Y 的卡诺图
令 A 1 = A A_1 = A A1=A、 A 0 = B A_0=B A0=B
要令 Y = F Y=F Y=F ,则 D 0 = 0 D_0=0 D0=0 , D 1 = D 2 = C D_1=D_2=C D1=D2=C, D 3 = 1 D_3=1 D3=1
-
Step4:画连线图








 本文详细解释了数据选择器如何构建组合逻辑函数,包括4选1数据选择器的逻辑表达式、数据选择器输出信号的特点、标准与或表达式以及用数据选择器如74LS151和74LS153实现逻辑函数的步骤,通过实例演示了两种求解方法:代数法和卡诺图法。
本文详细解释了数据选择器如何构建组合逻辑函数,包括4选1数据选择器的逻辑表达式、数据选择器输出信号的特点、标准与或表达式以及用数据选择器如74LS151和74LS153实现逻辑函数的步骤,通过实例演示了两种求解方法:代数法和卡诺图法。
















 6620
6620

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








