三维矩阵旋转、平移的左乘与右乘分析
在矩阵的初等变换中,矩阵的左乘代表着行变换,TA=B。
矩阵的右乘相当于列变换, AT=C。
当三维坐标发生旋转、平移时,就需要考虑到矩阵是左乘还是右乘。
设有旋转矩阵R,平移矩阵T, 坐标矩阵A。
-若是绕着静态的世界坐标系旋转,有RA,即左乘旋转矩阵
- 若是绕着动态的自身坐标系旋转,有A’R’, 即右乘旋转矩阵
- 若是进行平移,则有TA,即左乘平移矩阵, A’T’为右乘平移矩阵
在使用中,我们通常对三维点(云)的旋转与平移进行左乘。
而旋转矩阵在左乘时设逆时针为正。
以下是常用的旋转矩阵。
有列向量A=[x,y,z];
则 RA 就是对 A 进行旋转。注意这里 A 是列向量,因为是在对A的每行的元素进行变换。
若要写成右乘形式,则有(RA)’=A’R’,此时R’变为右乘的旋转矩阵,A’为行向量,对A’的每一列元素进行变换。
对于平移有平移矩阵T=
I0 u1
其中 u 为平移向量(x,y,z); I 为3X3的单位矩阵。
设有 列向量B,则对B进行平移为 TB,左乘形式。
右乘形式为 B’T’
旋转与平移的过程
设有 3x3旋转矩阵R, 平移列向量u,平移矩阵T 为上述表达形式, 坐标列向量A
以下过程用常见的左乘形式
1 先旋转再平移
RA+u = [ R , u ; 0 1]* [A , 1 ]
也可以写成 T*R*A 的形式, A为齐次坐标的形式
2 先平移再旋转
R(A+u)=RA+Ru;
也可以写成 R*T*A
若要将上述过程写成右乘的形式,则要全部进行转置









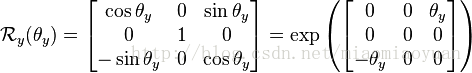















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








