统计文本建模的问题就是:追问这些观察到的语料库中的词序列是如何生成的。
1)LDA文本建模(1-2)里应该明白的结论
- beta分布是二项式分布的共轭先验概率分布:
- “对于非负实数
和
,我们有如下关系
- “对于非负实数
------------------(1)
其中
对应的是二项分布
的计数。针对于这种观测到的数据符合二项分布,参数的先验分布和后验分布都是Beta分布的情况,就是Beta-Binomial 共轭。”
- 狄利克雷分布(Dirichlet分布)是多项式分布的共轭先验概率分布:
- “ 把
从整数集合延拓到实数集合,从而得到更一般的表达式如下:
- “ 把
------------------(2)
针对于这种观测到的数据符合多项分布,参数的先验分布和后验分布都是Dirichlet 分布的情况,就是 Dirichlet-Multinomial 共轭。 ”
- 频率派和贝叶斯派思考问题的模式:
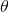 虽然是未知的,但最起码是确定的一个值。同时,样本X 是随机的,所以频率派重点研究样本空间,大部分的概率计算都是针对样本X 的分布;
虽然是未知的,但最起码是确定的一个值。同时,样本X 是随机的,所以频率派重点研究样本空间,大部分的概率计算都是针对样本X 的分布;
贝叶斯派 的观点则截然相反,他们认为待估计的 参数
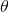 是随机变量,服从一定的分布
,而样本X 是固定的,由于样本是固定的,所以他们重点研究的是参数
是随机变量,服从一定的分布
,而样本X 是固定的,由于样本是固定的,所以他们重点研究的是参数
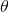 的分布。他们的思维模式是:
先验分布
的分布。他们的思维模式是:
先验分布
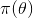 + 样本信息
+ 样本信息
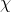
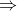








 本文介绍了LDA文本建模的基础,包括Unigram Model、Mixture of unigrams model和重点讲解的pLSA模型。pLSA模型中,文档由多个主题生成,每个主题在文档中出现的概率不同。LDA模型进一步改进,通过Dirichlet分布处理主题的不确定性。
本文介绍了LDA文本建模的基础,包括Unigram Model、Mixture of unigrams model和重点讲解的pLSA模型。pLSA模型中,文档由多个主题生成,每个主题在文档中出现的概率不同。LDA模型进一步改进,通过Dirichlet分布处理主题的不确定性。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 4417
4417

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








