笔者前面几篇文章讨论的是基于四元数的互补滤波算法,并单独对地磁计融合部分做了详细的讨论和解释。而本文讨论的姿态融合算法叫做梯度下降法,这部分代码可以参见Sebastian O.H. Madgwick在2010年4月发表的一篇论文(An efficient orientation filter for inertial andinertial/magneticsensor arrays),这篇论文利用四元数微分方程求解当前姿态,然后分别利用加速度计和地磁计进行补偿,推导出两种姿态融合算法。两种算法均为梯度下降法,而其中地磁计的处理方式笔者已经在《四元数姿态解算中的地磁计融合解读》一文中详细讨论了,这里笔者将对Madgwick对于加速度计和地磁计的梯度下降法做出详细的解释,期间一定有个人不足的地方,仅供参考,希望和各位网友一起学习!
首先来谈谈什么是梯度。维基百科中解释的是“标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率。”很显然,梯度和变化率有关。现在我们引入标量函数f(x),对标量函数f(x)求导,不难得到f’(x)就是梯度,就是曲线在某一点的斜率。梯度下降法就是我们顺着这个在某一点下降速度最快的反方向一直走,走到一个极值点,这个点就是最优解(稳定解)。
那么这个梯度的概念和我们的姿态解算有什么关系?
我在前面的文章中已经说明:我们求解姿态就是求解的转换矩阵(矩阵元素就是四元数)。这个转换矩阵是有误差的,我们所要做的工作就是采用某种算法,消除误差,最后得到的解就是我们的近似精确解,也就是姿态四元数了。消除误差四个字,在实际的实现过程中,是通过误差函数来实现的。定义误差函数ef(x),那么我们的工作就是令ef(x)=0,求解上述方程得到x的值。我们在求解高阶方程的时候,一般的方法就是求导,求极值点,根据这些值来判断精确值个数和位置。这是我们高中所学习到的知识,在这里是一样的。只不过,这里的误差函数ef(x)不再是之前讨论的简单的标量函数了,他的自变量x变成了向量[q0 q1 q2 q3]。这也就是说,原先的标量函数ef(q)变成了如今的标量函数ef([q0 q1 q2 q3]),他仍然是标量函数,但是自变量是向量[q0 q1 q2 q3]。
对上述自变量是向量的标量函数,我们要用梯度法求解,就必须求导。标量函数对向量求导很简单,只需要分别对向量中的各个变量求偏导即可:
但是,我们的姿态解算是三维姿态,不是一维姿态,所以,这里的ef(q)并不是一个标量函数,实质上是一个向量函数ef(q),这个向量函数里面有三个元素,分别对应xyz轴的三个分量,每个分量又由一个四元数向量q构成。那么现在就引入了一个较为复杂的误差函数ef(q),该误差函数不光自变量是一个向量,并且因变量也是一个向量,这种函数叫做多元向量函数。那么我们现在的问题就转化为求多元向量函数的极值问题。
针对上述极值问题,在计算机中,多采用数值解法,如最速下降法、牛顿法、共轭梯度法。我们这里讨论就是第一种算法,又叫做梯度下降法。PS:梯度下降法为一阶线性收敛,牛顿法为二阶线性收敛,所以从收敛速度和精度来讲牛顿法要好,但是需要计算Hessian矩阵,计算量大,笔者在这里就不细说了。(或许今后笔者会尝试牛顿法求解姿态)
在梯度下降法中,需要对多元向量函数求导,当然,前人已经研究过这个问题了,美其名曰雅可比矩阵(Jacobian)。不要被他吓到,雅可比矩阵就是按照规矩来一个个求导的过程。上述讨论了标量函数对向量的导数的情况,当标量函数变为向量时,只需要继续对每一个向量再求偏导即可。对于上式(假设四元数向量定义为行向量),再对每一个因变量求偏导:
上式就是多元向量函数的导数(也称为雅可比矩阵)。在这里,我定义的是行向量的四元数q和列向量因变量[efx efy efz]’,你同样可以定义列向量四元数q和行向量因变量[efx efy efz]。但是注意在求导的时候,注意一下矩阵的行列对应,记住:行向量不能对行向量求导,列向量不能对列向量求导,只能交错进行,这一点一定要记住!因为后面在用梯度计算姿态的时候为了满足矩阵乘法法则需要转置雅可比矩阵。
这里,我们由引例考虑实际情况。现在考虑陀螺仪和加速度计的梯度下降法姿态融合算法。
先给出梯度下降法计算公式:
从上述公式也可以看出梯度下降法属于一阶收敛,牛顿法在迭代公式中应用到了f(x)的导数,所以属于二阶收敛。对于上述公式的理解,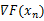

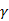
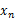

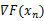








 本文深入探讨了四元数姿态解算中的梯度下降法,通过Sebastian O.H. Madgwick的论文,解释了如何利用加速度计和地磁计进行姿态融合。文章详细介绍了梯度的概念,以及如何通过梯度下降法求解四元数姿态的误差函数,同时讨论了雅可比矩阵在算法中的作用。还对比了梯度下降法与其他数值解法的优缺点,并提供了算法的实现流程和融合地磁计的扩展。
本文深入探讨了四元数姿态解算中的梯度下降法,通过Sebastian O.H. Madgwick的论文,解释了如何利用加速度计和地磁计进行姿态融合。文章详细介绍了梯度的概念,以及如何通过梯度下降法求解四元数姿态的误差函数,同时讨论了雅可比矩阵在算法中的作用。还对比了梯度下降法与其他数值解法的优缺点,并提供了算法的实现流程和融合地磁计的扩展。
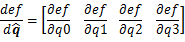

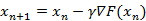
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 3162
3162

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








