信号与系统 拉普拉斯变换

拉普拉斯变换

拉普拉斯变换在整个学习过程中一般出现在大题中，所以这也是信号与系统中比较重要的知识点，下来我们学习一下相关内容。

1. 常见的拉普拉斯变换
2. 拉普拉斯逆变换
3. s域系统分析
4. 系统的s域框图
5. 单边拉氏变换与傅里叶变换
6. 拉普拉斯变换性质

1.常见的拉普拉斯变换

时域	s域
$\delta (t)$	$1,\sigma >-\infty$
${\delta }^{{}^{\prime }}(t)$	$s,\sigma >-\infty$
$\epsilon (t),1$	$\frac{1}{s},\sigma >0$
$e^{-s_{0}t}$	$\frac{1}{s+s_0},s_0={\sigma }_0+j{\omega }_0,\sigma >-{\sigma }_0$
$\cos {\omega }_{0}t=\frac{e^{j{\omega }_{0}t}+e^{-j{\omega }_{0}t}}{2}$	$\frac{s}{s^2+{\omega }_0^2}$
$\sin {\omega }_{0}t=\frac{e^{j{\omega }_{0}t}-e^{-j{\omega }_{0}t}}{2j}$	$\frac{{\omega }_0}{s^2+{\omega }_0^2}$
$g_{\tau }(t-\frac{\tau }{2})(g_{\tau }(t-\frac{\tau }{2})$在$0<t<\tau$范围内值为1，其余范围值为零。)	$\frac{1-e^{-s\tau }}{s},\sigma >-\infty$

对于有始周期信号$f_{\tau }(t)$

已知 $${\delta }_T(t)=\sum _{n=-\infty }^{\infty }\delta (t-nT)$$
求解$f_T(t)=f_{0}t\ast {\delta }_T(t)。$

则$$f_T(t)\leftrightarrow F_0(s)\cdot \sum _{n=0}^{\infty }{e}^{-nTs}$$
变换后可得
$$F_0(s)\cdot (1+e^{-Ts}+e^{-2Ts}+\dots )=F_0(s)\cdot \frac{1}{1-e^{-Ts}}$$

所以
$${\sum }_{n=0}^{\infty }\delta (t-nT)\leftrightarrow \frac{1}{1-e^{-sT}}$$

$${\sum }_{n=0}^{\infty }{f}_0(t-nT)\leftrightarrow \frac{F_0(s)}{1-e^{-Ts}}$$
注意这里求解的过程用到了拉普拉斯变换性质中的时移性质和时域卷积定理。
举个有关有始周期信号的例子，已知$\frac{1}{1-e^{-sT}}$,求其时域周期信号函数。

$$\frac{1}{1-e^{-sT}}=\frac{1-e^{-sT}}{1-e^{-2sT}}=(1-e^{-sT})\cdot \frac{1}{1-e^{-2sT}}$$

$$(1-e^{-sT})\cdot \frac{1}{1-e^{-2sT}}\leftrightarrow [\delta (t)-\delta (t-T)]\ast \sum _{n=0}^{\infty }\delta (t-2nT)$$
$$[\delta (t)-\delta (t-T)]\ast \sum _{n=0}^{\infty }\delta (t-2nT)=\sum _{n=0}^{\infty }\delta (t-2nT)-\sum _{n=0}^{\infty }\delta (t-(2n+1)T)$$

4.系统的s域框图

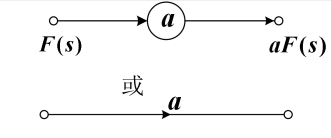
(1)数乘器

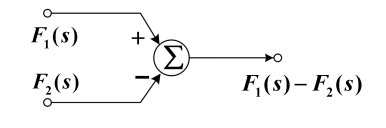
(2)加法器

(3)积分器

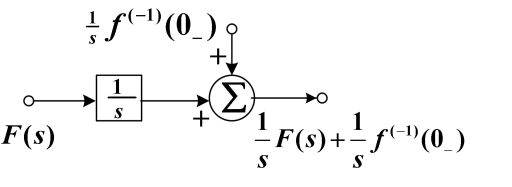
零状态时：

$\frac{1}{s}$是s域积分器的系统函数

5. 单边拉氏变换与傅里叶变换

$$F(s)={\int }_0^{\infty }f(t)e^{-st}dt,Re[s]>{\sigma }_0$$
$$F(j\omega )={\int }_{-\infty }^{\infty }f(t)e^{-j\omega t}dt$$
要对其关系进行讨论，f(t)必须为因果信号。
根据收敛坐标${\sigma }_0$的值可分为三种情况：
(1)${\sigma }_0<0$时，F(s)的收敛域包含$j\omega$轴。
$$F(j\omega )=F(s){|}_{s=j\omega }$$
(2)${\sigma }_0>0$时,$F(j\omega )$不存在。
举个例子

$$f(t)=e^{2t}\epsilon (t)\leftrightarrow F(s)=\frac{1}{s-2},\sigma >2$$
所以不存在。

(3)${\sigma }_0=0$时，即F(s)的收敛边界为$j\omega$轴。
$$F(j\omega )=\underset{\sigma \to 0}{\lim }F(s)$$
$$F(j\omega )=F(s){|}_{s=j\omega }+\sum _{i=1}^N\pi K_i\delta (\omega -{\omega }_i)$$
举个例子

$$当f(t)=\epsilon (t)\leftrightarrow F(s)=\frac{1}{s}$$
$$F(j\omega )=F(s){|}_{s=j\omega }+\pi \delta (\omega )=\frac{1}{j\omega }+\pi \delta (\omega )$$