Lyapunov

为争。

已于 2023-06-21 15:15:56 修改

阅读量2.8k

点赞数 3

文章标签：学习

于 2023-04-21 11:01:53 首次发布

本文链接：https://blog.csdn.net/ohhjack/article/details/130282689

版权

一、正定函数

令 $V(x)$ 是向量x的标量函数，S是x空间包含原点的封闭有限区域，如果对于S中所有的x，都有：

（1） $\dfrac{\partial}{\partial x}V(x)$ 存在且连续

（2） $V(0)=0$

（3）当 $x\neq 0$ 时， $V(x)> 0,(V(x)\geq 0))$

则V(x)是正定的（半正定）的。

二、二次型

1、定义

在李雅普诺夫第二方法上的稳定性分析中，二次型函数起着重要作用： $V(x)={x}^T{P}{x}$ ，P为n*n有权阵，则有：

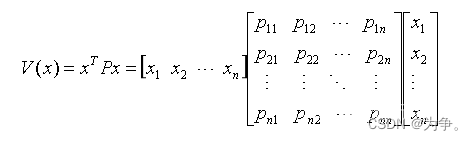
即： $V(\mathbf{x})=\sum_{i=1}^{n}\sum_{j=1}^{n}\boldsymbol{p}_{ij}\boldsymbol{x}_{i}\boldsymbol{x}_{j}$ ，其中P为对称矩阵，即Pij=Pji。

2、判定

根据塞尔维斯特定理， $V(x)={x}^T{P}{x}$ 中的P为对称矩阵时， $V(x)$ 正定的充要条件是P的所有顺序主子式行列式都是正的，即：

如果P的所有主子式为非负的，那么 $V(x)$ 为半正定的。

三、连续时间系统Lyapunov稳定性分析

1、李雅普诺夫第一法

线性系统：求出系统矩阵的特征值即可判断系统的稳定性。

非线性系统：由系统的动态方程来找出其一次近似的线性化方程，在通过对线性化方程的稳定性分析而给出原非线性系统在小范围内稳定性的有关信息。

定义：某一线性时不变系统在这里插入图片描述，如果系统矩阵A的特征值全部在左半平面，即特征值都小于0，即A的所有特征值都具有负实部，则系统的平衡状态 Xe 是渐近稳定的。

2、李雅普诺夫第二法

通过构造一个Lyapunov函数，分析其与其一次倒数的正定性而确定其稳定性。

定义：某一线性时不变系统：在这里插入图片描述，A为n×n常数非奇异矩阵，对于任意的正定矩阵Q，系统在平衡状态x=0处是大范围渐近稳定的充分必要条件是：

存在一个正定的实对称阵P，满足李雅普诺夫(矩阵代数)方程：在这里插入图片描述
先设定Lyapunov函数，再得到Lyapunov方程，最后去分析稳定性。

3、举例

（1）第一法

>> A=[-3 -6 -2 -1;1 0 0 0;0 1 0 0;0 0 1 0];
>> B=[1;0;0;0];C=[0 0 1 1];D=[0];


>> eig(A)

ans =

  -1.3544 + 1.7825i
  -1.3544 - 1.7825i
  -0.1456 + 0.4223i
  -0.1456 - 0.4223i

（2）第二法

A=[1 -3.5 4.5;2 -4.5 4.5;-1 1.5 -2.5];
B=[-0.5;-0.5;-0.5]';C=[1 0 1]; %系统状态方程
Q=eye(3,3);  %Q=I
P=lyap(A,Q); %求解矩阵P

for i=1:length(A)  %判断是否稳定
 det(P(1:i,1:i))
end

ans =

    1.4825


ans =

    0.6725


ans =

    0.1169

即所有顺序主子式均大于0，系统稳定。

四、离散时间系统Lyapunov稳定性分析

1、稳定性判断

在这里插入图片描述
（1）第一方法：第一方法：A的特征值模均小于1；
（2）第二方法：对于任意的正定矩阵Q，存在正定矩阵P满足Lyapunov方程：

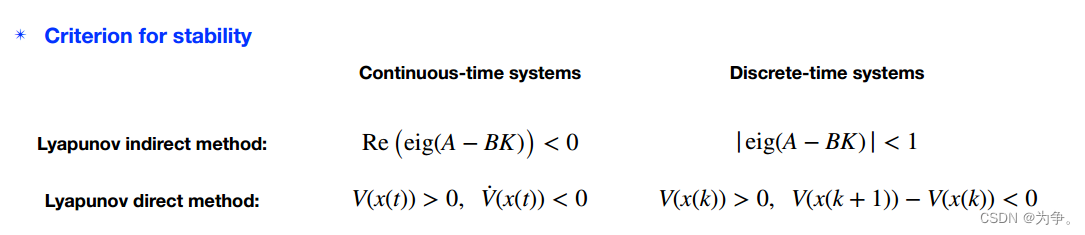
2、离散Lyapunov的解

注意右侧Q多出KTRK

MATLAB求解

（1）写入初始参数

>> A=[1.1 2;0 0.95];
>> B=[0;0.079];
>> Q=eye(2);
>> R=.1;

（2）利用离散lqr求得最优反馈参数

>> [K,P,r]=dlqr(A,B,Q,R);

K =

    2.4950   12.5106

（3）根据离散Lyapunov方程，可知此方程的“Q”为Q+KTRK

>> Q2=Q+K'*R*K

(4)判断系统稳定性

>> Acl=A-B*K
>> eig(Acl)


>> abs(0.5308 + 0.2651i)
>> abs(0.5308 - 0.2651i)

可知极点的模均小于1，在单位圆内，则系统稳定。

（5）解Lyapunov方程

>> P=dlyap(Acl',Q2)

P =

    4.0373    8.5226
    8.5226   31.5400

五、无约束MPC

1、输入变量

>> A=[1.1 2;0 0.95]
>> B=[0;0.079]
>> Q=eye(2)
>> R=0.1

2、利用dlqr求解最优反馈矩阵K

>> [K,P,r]=dlqr(A,B,Q,R)

3、根据Lyapunov求解可知闭环系统矩阵Q2=Q+K的转置RK

>> Q2=Q+K'*R*K

4、求解闭环系统矩阵Acl

>> Acl=A-B*K

5、求解特征值，判断系统是否稳定

>> eig(Acl)

求特征值的模，可知特征值在单位圆内，系统稳定。

>> y=abs(0.5308 + 0.2651i)
>> y=abs(0.5308 - 0.2651i)

6、求解Lyapunov方程

>> P=dlyap(Acl',Q2)

7、求解反馈矩阵Kmpc

Q_=diag（Q,Q,Q,...,P）

R_=diag（R,R,R,...,R）

>> Q_=[eye(2),zeros(2),zeros(2),zeros(2);zeros(2),eye(2),zeros(2),zeros(2);zeros(2),zeros(2),eye(2),zeros(2);zeros(2),zeros(2),zeros(2),P]

>> R_=[0.1 0 0 0;0 0.1 0 0;0 0 0.1 0;0 0 0 0.1]

8、求F与FAI

F=[A;A2;A3;...AN]

>> F=[A;A*A;A*A*A;A*A*A*A]

FAI=[B ...;AB B ...;A2B AB ....;AN-1B AN-2B ...B];

>> L=[0;0]
>> FAI=[B L L L;A*B B L L;A*A*B A*B B L;A*A*A*B A*A*B A*B B]

9、求Kmpc

>> K=inv(FAI'*Q_*FAI+R_)*FAI'*Q_*F

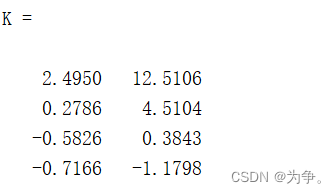
取第一个值，则u(k)=-[2.459 12.5106]x(k)

为争。

关注

3
点赞
踩
17

收藏

觉得还不错? 一键收藏
0
评论
Lyapunov

取第一个值，则u(k)=-[2.459 12.5106]x(k)求特征值的模，可知特征值在单位圆内，系统稳定。3、根据Lyapunov求解可知闭环系统矩阵。2、利用dlqr求解最优反馈矩阵K。5、求解特征值，判断系统是否稳定。4、求解闭环系统矩阵Acl。6、求解Lyapunov方程。7、求解反馈矩阵Kmpc。
复制链接

扫一扫