C++的数据结构与算法(六)二叉树搜索算法学习

1.二分搜索树原理

1.1 理论介绍

同上篇文章介绍的二叉堆本质上类似，都是一个二叉树。选择什么特征的二叉树是根据具体问题来决定的，了解一下二分搜索树的特点:

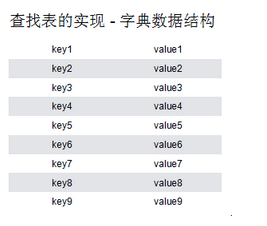
• （1）查找表的实现 - 字典数据结构

查找表的实现，通常这种实现又被称为“字典数据结构”，都是以键值对形式形成了表，通过key来查找对应value。如果这些key值都是整型，那么可以使用数组实现，但是在实际运用中key值是比较复杂的，例如字典。因此需要实现一个“查找表”，最基础方式就是二分搜索树。

• （2）时间复杂度比较

通过以上分析，其实普通数组和顺序数组也可以完成以上需求，但是操作起来消耗的时间却不尽人意。

• (3）高效性

不仅可查找数据，还可以高效地插入，删除数据之类的动态维护数据。

• (4) 定义

动态数据结构
是一颗二叉树
每个节点的值都大于其左子树的所有节点的值
每个节点的值都小于其右子树的所有节点的值
以左右孩子为根的子树仍为二分搜索树

1.2代码实现

在代码实现堆时，正是因为它是一棵完全的二叉树此特点，所以可使用数组进行实现，但是二分搜索树并无此特性，所以在实现上是设立key、value这种Node节点，节点之间的连续使用指针。

• Node节点结构体包含：

  Key key;
  Value value;
  Node *left; //左孩子节点指针
  Node *right; //右孩子节点指针

• 私有成员变量：

  Node *root; // 根节点
  int count; // 节点个数

• 公有基本方法：

  BST() // 构造函数, 默认构造一棵空二分搜索树
  int size() // 返回二分搜索树的节点个数
  bool isEmpty() // 返回二分搜索树是否为空

// 二分搜索树
template <typename Key, typename Value>
class BST{

private:
    // 二分搜索树中的节点为私有的结构体, 外界不需要了解二分搜索树节点的具体实现
    struct Node{
        Key key;
        Value value;
        Node *left;
        Node *right;

        Node(Key key, Value value){
            this->key = key;
            this->value = value;
            this->left = this->right = NULL;
        }
    };

    Node *root; // 根节点
    int count;  // 节点个数

public:
    // 构造函数, 默认构造一棵空二分搜索树
    BST(){
        root = NULL;
        count = 0;
    }
    ~BST(){
        // TODO: ~BST()
    }

    // 返回二分搜索树的节点个数
    int size(){
        return count;
    }

    // 返回二分搜索树是否为空
    bool isEmpty(){
        return count == 0;
    }
};

2.二分搜索树的节点插入

2.1算法原理

这部分也是构建二叉树的关键步骤
由于二分搜索树本身的递归特性, 所以可以很方便的使用递归实现向二分搜索树中添加元素, 步骤如下:
定义一个公共的add方法, 用于添加元素
定义一个递归的add方法用于实际向二分搜索树中添加元素
查看以下动画演示了解插入新节点的算法思想：

2.2代码实现

判断node节点是否为空，为空则创建节点并将其返回（ 判断递归到底的情况）。
若不为空，则继续判断根元素的key值是否等于根元素的key值：
若相等则直接更新value值即可。
若不相等，则根据其大小比较在左孩子或右孩子部分继续递归直至找到合适位置为止。

public:
    // 向二分搜索树中插入一个新的(key, value)数据对
    void insert(Key key, Value value){
        root = insert(root, key, value);//递归
    }
 
private:
    // 向以node为根的二叉搜索树中,插入节点(key, value)
    // 返回插入新节点后的二叉搜索树的根
    Node* insert(Node* node, Key key, Value value){
        if( node == NULL ){//直到子树为空，新建一个
            count += 1;
            return new Node(key, value);
        }

        if( key == node->key )
            node->value = value;//赋值
        else if( key < node->key )
            node->left = insert(node->left, key, value);//递归
        else // key > node->key
            node->right = insert(node->right, key, value);//递归

        return node;//结束insert()函数返回值
    }

3.二分搜索树的查找

其实在理解二分搜索树的插入过程后，其查找过程本质上是相同的，这里提供两个搭配使用的查找函数：
bool contain(Key key)：查看二分搜索树中是否存在键key
Value* search(Key key)：在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回NULL。（注意：这里返回值使用Value* ，就是为了避免用户查找的值并不存在而出现异常）

public:
   // 查看二分搜索树中是否存在键key
    bool contain(Key key){
        return contain(root, key);
    }

    // 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回NULL
    Value* search(Key key){
        return search( root , key );
    }

private:
    // 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法
    bool contain(Node* node, Key key){

        if( node == NULL )
            return false;

        if( key == node->key )
            return true;
        else if( key < node->key )
            return contain( node->left , key );
        else // key > node->key
            return contain( node->right , key );
    }

    // 在以node为根的二分搜索树中查找key所对应的value, 递归算法
    // 若value不存在, 则返回NULL
    Value* search(Node* node, Key key){

        if( node == NULL )
            return NULL;

        if( key == node->key )
            return &(node->value);
        else if( key < node->key )
            return search( node->left , key );
        else // key > node->key
            return search( node->right, key );
    }
};

4.二分搜索树的遍历(深度优先遍历)

4.1算法原理

二分搜索树的前中后序遍历：
对于每个节点而言，可能会有左、右两个孩子，所以分成下图中3个点，每次递归过程中会经过这3个点:

前序遍历：先访问当前节点，再依次递归访问左右子树

中序遍历：先递归访问左子树，再访问自身，再递归访问右子树

后续遍历：先递归访问左右子树，再访问自身节点

4.2代码实现

//前序遍历
public:
    // 二分搜索树的前序遍历
    void preOrder(){
        preOrder(root);
    }

private:
    // 对以node为根的二叉搜索树进行前序遍历, 递归算法
    void preOrder(Node* node){
        if( node != NULL ){
            cout<<node->key<<endl;
            preOrder(node->left);
            preOrder(node->right);
        }
    }
//中序遍历
public:
    // 二分搜索树的中序遍历
    void inOrder(){
        inOrder(root);
    }

private:
    // 对以node为根的二叉搜索树进行中序遍历, 递归算法
    void inOrder(Node* node){

        if( node != NULL ){
            inOrder(node->left);
            cout<<node->key<<endl;
            inOrder(node->right);
        }
    }
//后序遍历
public:
    // 二分搜索树的后序遍历
    void postOrder(){
        postOrder(root);
    }

private:
    // 对以node为根的二叉搜索树进行后序遍历, 递归算法
    void postOrder(Node* node){

        if( node != NULL ){
            postOrder(node->left);
            postOrder(node->right);
            cout<<node->key<<endl;
        }
    }

以上所有深度优先遍历代码实现可分为3个步骤：
每次都递归到底,所以又叫深度遍历!!

递归左孩子
递归右孩子
打印自身
以上遍历只是交换了这3个步骤的执行顺序。 

5.层序遍历(广度优先遍历)

5.1算法原理

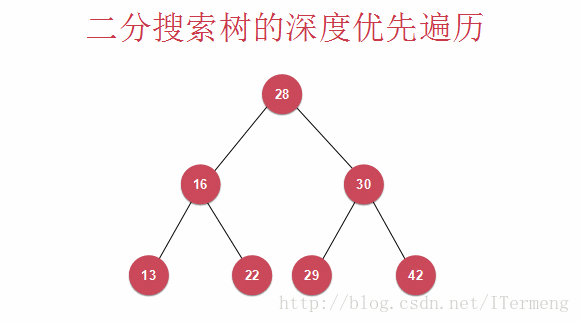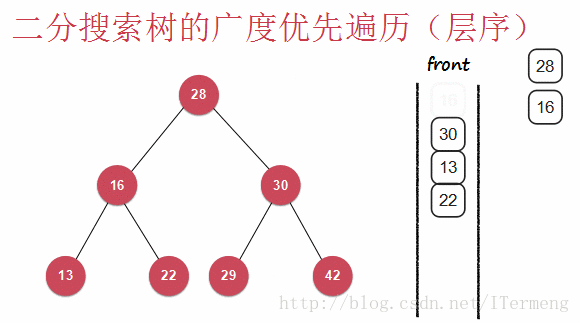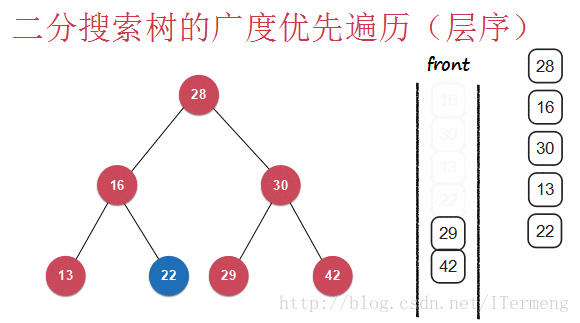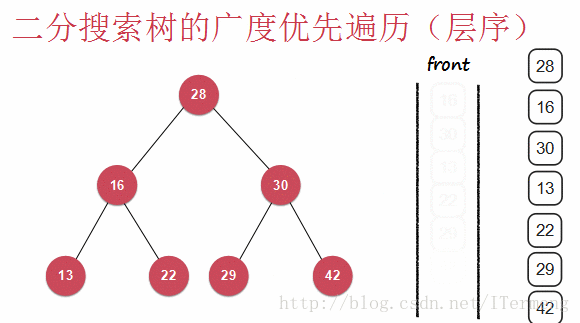
和深度遍历不一样,广度优先遍历则是层序遍历(广度优先遍历)，一层一层地向下遍历，查看以下动画：

5.3代码实现

查看以上动画，实现其过程需要引入先进先出的“队列”数据结构。首先将28入队，第一层遍历完毕，可进行操作，将28出队并打印。遍历第二层16、30依次入队，再出队进行打印操作。最后13，22入队，29，42入队,再出队进行打印操作。

public:
    // 二分搜索树的层序遍历
    void levelOrder(){

        queue<Node*> q;
        q.push(root);//入队根节点
        while( !q.empty() ){//队列为空时结束循环

            Node *node = q.front();//获取队首元素
            q.pop();

            cout<<node->key<<endl;

            if( node->left )
                q.push( node->left );
            if( node->right )
                q.push( node->right );
        }
    }

6.删除最大值，最小值、删除节点

6.1删除最大值，最小值算法原理和代码实现

二分搜索树中最复杂的操作——删除节点，其实此过程中的查找需删除节点和删除操作并不复杂，复杂的是如何操作删除之后节点的左右孩子，使得最后整棵树依然保持二分搜索树的性质。
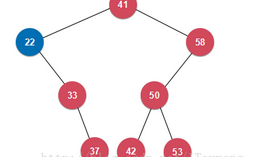
首先来了解最简单的情况—–删除二分搜索树的最小值和最大值，其实此过程根据搜索树的特征很容易解决，从根节点开始遍历其左孩子，直至最后节点无左孩子，那么此节点就是最小值；最大值同理，遍历其右孩子即可。
注意，这里二分搜索数的最小、大值并非一定完全二叉树下的情况，例如下图，所以在删除节点时，需要将其左孩子或右孩子代替其删除节点，来保持二分搜索树的特征。
举个例子，需要删除下图二分搜索树的最小值22，删除22后，22必然没有左孩子，因为它已经是最小值，将其右孩子33代替22的位置，返回节点33。删除最大值同理

public:
    // 寻找二分搜索树的最小的键值
    Key minimum(){
        assert( count != 0 );
        Node* minNode = minimum( root );
        return minNode->key;
    }

    // 寻找二分搜索树的最大的键值
    Key maximum(){
        assert( count != 0 );
        Node* maxNode = maximum(root);
        return maxNode->key;
    }

    // 从二分搜索树中删除最小值所在节点
    void removeMin(){
        if( root )
            root = removeMin( root );
    }

    // 从二分搜索树中删除最大值所在节点
    void removeMax(){
        if( root )
            root = removeMax( root );
    }

private:
        // 返回以node为根的二分搜索树的最小键值所在的节点
    Node* minimum(Node* node){
        if( node->left == NULL )
            return node;

        return minimum(node->left);
    }

    // 返回以node为根的二分搜索树的最大键值所在的节点
    Node* maximum(Node* node){
        if( node->right == NULL )
            return node;

        return maximum(node->right);
    }

    // 删除掉以node为根的二分搜索树中的最小节点
    // 返回删除节点后新的二分搜索树的根
    Node* removeMin(Node* node){

        if( node->left == NULL ){

            Node* rightNode = node->right;
            delete node;
            count --;
            return rightNode;
        }

        node->left = removeMin(node->left);
        return node;
    }

    // 删除掉以node为根的二分搜索树中的最大节点
    // 返回删除节点后新的二分搜索树的根
    Node* removeMax(Node* node){

        if( node->right == NULL ){

            Node* leftNode = node->left;
            delete node;
            count --;
            return leftNode;
        }

        node->right = removeMax(node->right);
        return node;
    }

6.1删除任意值算法原理和代码实现

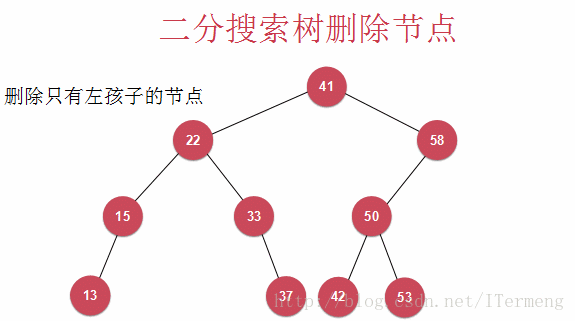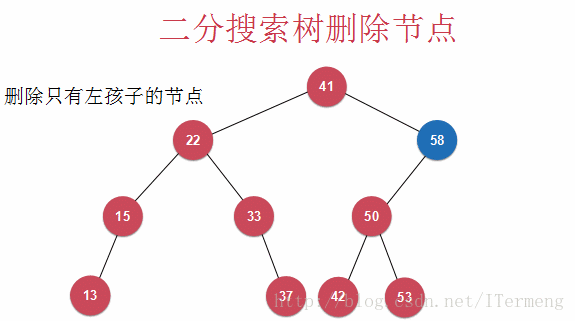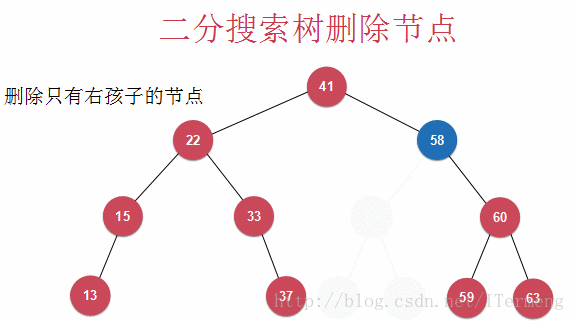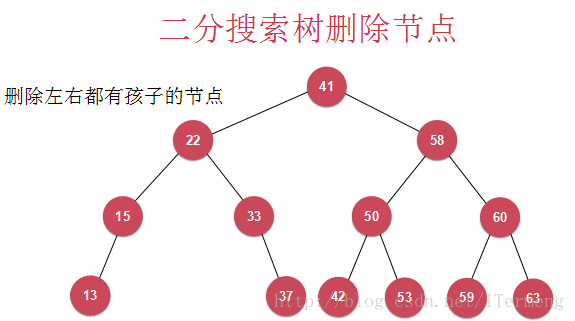
以上是删除节点的特殊情况，可以确定待删除节点只有1个孩子或者没有，所以在删除此节点之后，其孩子可以顶替，这样仍维护了二分搜索树的特征，如下图示例：

删除节点58同时拥有左、右孩子就要用到Hubbard Deletion
以下介绍的算法被称为Hubbard Deletion，在之前的讨论中，若待删除节点只有一个孩子，则用此孩子替代待删除节点；若有两个孩子，其思想也是类似，找到一个合适的节点来替代，而Hubbard Deletion算法则认为此替代节点是右子树的最小节点！
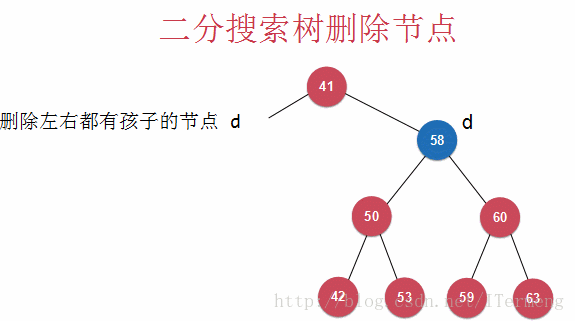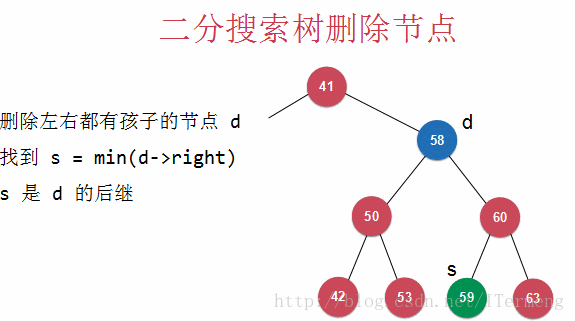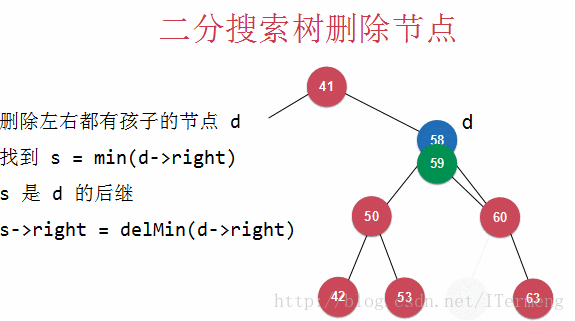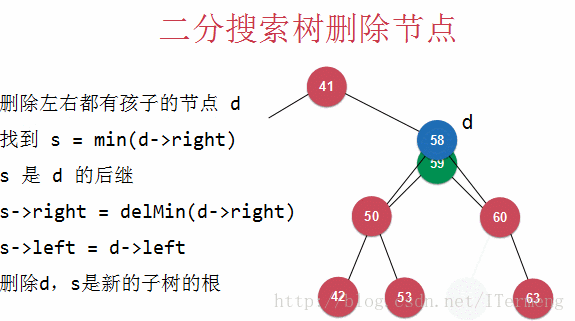
因此，需要代替58的节点是59，注意二分搜索树的特征，59的所有右孩子都比58要大，所以右孩子子树中的最小值59代替其58后，此二分搜索树的特征仍然成立！

  找到 s = min(d->right)，s 是 d 右子树中的最小值，需要代替d的后继节点
    s->right = delMin(d->right)
    s->left = d->left
    删除d，s是新的子树的根

public:
    // 从二分搜索树中删除键值为key的节点
    void remove(Key key){
        root = remove(root, key);
    }

private:
    // 删除掉以node为根的二分搜索树中键值为key的节点, 递归算法
    // 返回删除节点后新的二分搜索树的根
    Node* remove(Node* node, Key key){

        if( node == NULL )
            return NULL;//未找到对应key的节点

        if( key < node->key ){//在node的左子树中寻找
            node->left = remove( node->left , key );
            return node;
        }
        else if( key > node->key ){//在node的右子树中寻找
            node->right = remove( node->right, key );
            return node;
        }
        else{   // key == node->key

            // 待删除节点左子树为空的情况
            if( node->left == NULL ){
                Node *rightNode = node->right;
                delete node;
                count --;
                return rightNode;
            }

            // 待删除节点右子树为空的情况
            if( node->right == NULL ){
                Node *leftNode = node->left;
                delete node;
                count--;
                return leftNode;
            }

            // 待删除节点左右子树均不为空的情况
            // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
            // 用这个节点顶替待删除节点的位置
            Node *successor = new Node(minimum(node->right));
            count ++;

            successor->right = removeMin(node->right);
            successor->left = node->left;

            delete node;
            count --;

            return successor;
        }
    }

7.二分搜索树的顺序性

8.二分搜索树的局限性

9.二分搜索树总结